VnDoc.com

Cách giải các dạng bài tập động lực học Vật lý 10

Phương pháp động lực học

Bài trước

Tải về

Bài sau

Lớp: Lớp 10

Môn: Vật Lý

Dạng tài liệu: Chuyên đề

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Phương pháp giải bài tập động lực học Vật lý 10

Trong chương trình Vật lý 10, động lực học là phần kiến thức trọng tâm, giúp học sinh hiểu mối quan hệ giữa lực – khối lượng – gia tốc và là nền tảng để giải hầu hết các bài toán cơ học. Tuy nhiên, việc nhận dạng dạng bài và lựa chọn phương pháp phù hợp vẫn là khó khăn với nhiều học sinh.

Bài viết Cách giải các dạng bài tập động lực học Vật lý 10 tổng hợp phương pháp động lực học theo từng dạng bài, giúp học sinh nắm quy trình giải nhanh – hạn chế sai sót – nâng cao hiệu quả học tập.

A. Bài toán thuận

Biết các lực tác dụng: ${\overrightarrow{F}}_{1},{\overrightarrow{F}}_{1},...{\overrightarrow{F}}_{n}$ . Xác định chuyển động: a, v, s, t

Phương pháp giải:

Bước 1: Chọn hệ quy chiếu thích hợp.

Bước 2: Vẽ hình – Biểu diễn các lực tác dụng lên vật

Bước 3: Xác định gia tốc từ định luật II Newton

${\overrightarrow{F}}_{hl} = {\overrightarrow{F}}_{1} + {\overrightarrow{F}}_{2} + ... = m\overrightarrow{a}$ (1)

Chiếu (1) lên các trục toạ độ suy ra gia tốc a: $a = \frac{F_{hl}}{m}$ (2)

Bước 4: Từ (2), áp dụng những kiến thức động học, kết hợp điều kiện đầu để xác định v, t, s

B. Bài toán ngược

Biết chuyển động: v, t, s. Xác định lực tác dụng

Phương pháp giải:

Bước 1: Chọn hệ quy chiếu thích hợp.

Bước 2: Xác định gia tốc a dựa vào chuyển động đã cho (áp dụng phần động học)

Bước 3: Xác định hợp lực tác dụng vào vật theo định luật II Niutơn

F_hl = ma

Bước 4: Biết hợp lực ta suy ra các lực tác dụng vào vật.

C. Một số bài toán thường gặp

Bài toán 1: (Chuyển động của vật trên mặt phẳng ngang không có lực kéo)

Một ô tô đang chuyển động với vận tốc v₀ thì hãm phanh; biết hệ số ma sát trượt giữa ô tô và sàn là μ:

Gia tốc của ô tô là: a = -μg.

Bài toán 2: (Chuyển động của vật trên mặt phẳng ngang có lực kéo F)

Cho cơ hệ như hình vẽ.

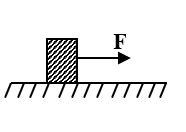
Cho lực kéo F, khối lượng của vật m.

- Nếu bỏ qua ma sát thì gia tốc của vật là: $a = \frac{F}{m}$

- Nếu hệ số ma sát giữa vật và sàn là $\mu$ thì gia tốc của vật là: $a = \frac{F - \mu mg}{m}$

Bài toán 3: (Chuyển động của vật trên mặt phẳng ngang phương của lực kéo hợp với phương ngang một góc α)

Cho cơ hệ như hình vẽ.

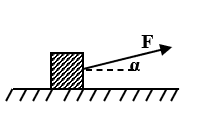
Cho lực kéo F, khối lượng của vật m, góc α.

- Nếu bỏ qua ma sát thì gia tốc của vật là: $a = \frac{F\cos\alpha}{m}$

- Nếu hệ số ma sát giữa vật và sàn là μ thì gia tốc của vật là: $a = \frac{F\cos\alpha - \mu\left( mg - F\sin\alpha \right)}{m}$

Bài toán 4: (Vật trượt trên mặt phẳng nghiêng từ trên xuống)

Một vật bắt đầu trượt từ đỉnh một mặt phẳng nghiêng, góc nghiêng α, chiều dài mặt phẳng nghiêng là l:

- Nếu bỏ qua ma sát

Gia tốc của vật: a = gsinα
Vận tốc tại chân mặt phẳng nghiêng: $v = \sqrt{2g\sin\alpha.l}$

- Nếu ma sát giữa vật và mặt phẳng nghiêng là μ

Gia tốc của vật: a = g(sinα - μcosα)
Vận tốc tại chân mặt phẳng nghiêng: $v = \sqrt{2g\left( \sin\alpha - \mu\cos\alpha \right)}.l$

Bài toán 5: (Vật trượt trên mặt phẳng nghiêng từ dưới lên)

Một vật đang chuyển động với vận tốc v₀ theo phương ngang thì trượt lên một phẳng nghiêng, góc nghiêng α:

- Nếu bỏ qua ma sát

Gia tốc của vật là: a = - gsinα
Quãng đường đi lên lớn nhất: $s_{\max} = \frac{v_{0}^{2}}{2g\sin\alpha}$

- Nếu hệ số ma sát giữa vật và mặt phẳng nghiêng là μ

Gia tốc của vật là: $a = - g\left( \sin\alpha + \mu\cos\alpha \right)$
Quãng đường đi lên lớn nhất: $s_{\max} = \frac{v_{0}^{2}}{2g\left( \sin\alpha + \mu\cos\alpha \right)}$

Bài toán 6: (Chuyển động của hệ hai vật trên mặt phẳng ngang)

Cho cơ hệ như hình vẽ. Cho F, m₁, m₂

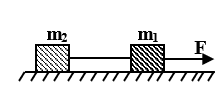
Nếu bỏ qua ma sát

+ Gia tốc của vật là: $a = \frac{F}{m_{1} + m_{2}}$

+ Lực căng dây nối: $T = m_{2}.\frac{F}{m_{1} + m_{2}}$

- Nếu ma sát giữa m₁; m₂ với sàn lần lượt là μ₁ và μ₂:

+ Gia tốc của m₁ và m₂: $a = \frac{F - \mu_{1}m_{1}g - \mu_{2}m_{2}g}{m_{1} + m_{2}}$

+ Lực căng dây nối: $T = m_{2}\frac{F - \mu_{1}m_{1}g - \mu_{2}m_{2}g}{m_{1} + m_{2}}$

Bài toán 7: (Chuyển động của hệ vật vắt qua ròng rọc cố định chuyển động theo hai phương khác nhau)

Cho cơ hệ như hình vẽ. Cho khối lượng m₁; m₂

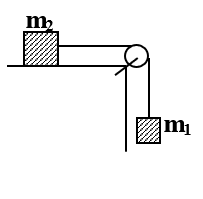
- Nếu bỏ qua ma sát

+ Gia tốc của m₁, m₂ là: $a = \frac{m_{1}g}{m_{1} + m_{2}}$

+ Lực căng dây nối: $T = m_{2}.\frac{m_{1}g}{m_{1} + m_{2}}$

- Nếu hệ số ma sát giữa m₂ và sàn là μ

+ Gia tốc của m₁, m₂ là: $a = \frac{\left( m_{1} - \mu m_{2} \right)g}{m_{1} + m_{2}}$

+ Lực căng dây nối: $T = m_{2}.\frac{\left( m_{1} - \mu m_{2} \right)g}{m_{1} + m_{2}}$

Chú ý: Nếu m₁ đổi chỗ cho m₂:

- Nếu bỏ qua ma sát

+ Gia tốc của m₁, m₂ là: $a = \frac{m_{2}g}{m_{1} + m_{2}}$

+ Lực căng dây nối: $T = m_{1}.\frac{m_{2}g}{m_{1} + m_{2}}$

- Nếu hệ số ma sát giữa m₁ và sàn là μ

+ Gia tốc của m₁, m₂ là: $a = \frac{\left( m_{2} - \mu m_{1} \right)g}{m_{1} + m_{2}}$

+ Lực căng dây nối: $T = m_{2}.\frac{\left( m_{2} - \mu m_{1} \right)g}{m_{1} + m_{2}}$

Bài toán 8: (Chuyển động của hệ vật nối với ròng rọc số định chuyển động cùng phương)

Cho cơ hệ như hình vẽ. Biết m₁, m₂.

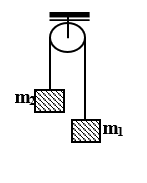
- Gia tốc của m₁: $a_{1} = \frac{\left( m_{1} - m_{2} \right)g}{m_{1} + m_{2}}$

- Gia tốc của m₂: $a_{2} = \frac{\left( m_{2} - m_{1} \right)g}{m_{1} + m_{2}}$

- Lực căng dây nối: $T = \frac{2m_{1}^{2}g}{m_{1} + m_{2}}$

Bài toán 9: (Hệ hai vật nối với ròng rọc cố định trên mặt phẳng nghiêng)

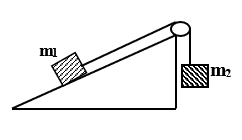
- Nếu bỏ qua ma sát:

* Trường hợp 1: Nếu m₁gsinα > m₂g. khi đó m₁ đi xuống m₂ đi lên

+ Gia tốc của m₁; m₂ là: $a = \frac{g\left( m_{1}\sin\alpha - m_{2} \right)}{m_{1} + m_{2}}$

+ Lực căng dây nối: $T = m_{2}g\left\lbrack 1 + \frac{m_{1}\sin\alpha - m_{2}}{m_{1} + m_{2}} \right\rbrack$

* Trường hợp 2: Nếu m₁gsinα < m₂g, khi đó m₁ đi lên m₂ đi xuống

+ Gia tốc của m₁; m₂ là: $a = \frac{g\left( m_{2} - m_{1}\sin\alpha \right)}{m_{1} + m_{2}}$

+ Lực căng dây nối: $T = m_{2}g\left\lbrack 1 - \frac{m_{2} - m_{1}\sin\alpha}{m_{1} + m_{2}} \right\rbrack$

- Nếu hệ số ma sát giữa m₁ và sàn là μ

Trường hợp 1: Nếu m₁gsinα > m₂g. khi đó m₁ đi xuống m₂ đi lên

+ Gia tốc của m₁; m₂ là: $a = \frac{g\left( m_{1}\sin\alpha - \mu m_{2}cos\alpha - m_{2} \right)}{m_{1} + m_{2}}$

+ Lực căng dây nối: $T = m_{2}g\left\lbrack 1 + \frac{m_{1}\sin\alpha - \mu m_{2}cos\alpha - m_{2}}{m_{1} + m_{2}} \right\rbrack$

Bài toán 10: Cho cơ hệ như hình vẽ. Cho m₁; m₂,

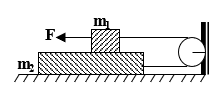
- Bỏ qua mọi ma sát:

+ Gia tốc của m₁ và m₂: $a = \frac{F}{m_{1} + m_{2}}$ (với a₁=-a₂ =a)

+ Lực căng dây nối: $T = m_{2}\frac{F}{m_{1} + m_{2}}$

- Cho hệ số ma sát giữa m₁ và m₂ là $\mu_{1}$ , giữa m₂ và sàn μ₂

Gia tốc của m₁ và m₂: $a = \frac{F - 2\mu_{1}m_{1}g - \mu_{2}m_{2}g}{m_{1} + m_{2}}$ (với a₁ = -a₂ = a)

Bài toán 11: Cho cơ hệ như hình vẽ. Cho m₁, m₂, F

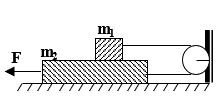
- Nếu bỏ qua ma sát

+ Gia tốc của m₁ và m₂: $a = \frac{F}{m_{1} + m_{2}}$ với a₂= -a₁ = a

+ Lực căng dây nối: $T = m_{1}\frac{F}{m_{1} + m_{2}}$

- Cho hệ số ma sát giữa m₁ và m₂ là $\mu_{1}$ , giữa m₂ và sàn μ₂

Gia tốc của m₁ và m₂: $a = \frac{F - 2\mu_{1}m_{1}g - \mu_{2}m_{2}g}{m_{1} + m_{2}}$ (với a₂ = -a₁ = a)

Bài toán 12: Cho cơ hệ như hình vẽ cho F, m₁, m₂.

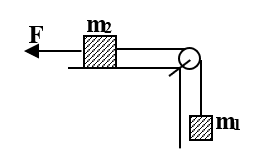
- Bỏ qua ma sát:

Trường hợp: F>m₁g $\Rightarrow$ m₁ đi lên

+ Gia tốc của m₁, m₂: $a = \frac{F - m_{1}g}{m_{1} + m_{2}}$

+ Lực căng dây nối: $T = m_{1}\left( g + \frac{F - m_{1}g}{m_{1} + m_{2}} \right)$

Trường hợp 2: F < m₁g $\Rightarrow$ m₁ đi xuống

+ Gia tốc của m₁, m₂: $a = \frac{m_{1}g - F}{m_{1} + m_{2}}$

+ Lực căng dây nối: $T = m_{1}\left( g + \frac{m_{1}g - F}{m_{1} + m_{2}} \right)$

- Hệ số ma sát giữa m₂ và sàn là μ

Trường hợp: F > m₁g $\Rightarrow$ m₁ có xu hướng đi lên

+ Gia tốc của m₁, m₂: $a = \frac{F - m_{1}g - \mu m_{2}g}{m_{1} + m_{2}}$

+ Lực căng dây nối: $T = m_{1}\left( g + \frac{F - m_{1}g - \mu m_{2}g}{m_{1} + m_{2}} \right)$

Trường hợp 2: F < m₁g $\Rightarrow$ m₁ đi xuống

- Gia tốc của m₁, m₂: $a = \frac{m_{1}g - F - \mu m_{2}g}{m_{1} + m_{2}}$

- Lực căng dây nối: $T = m_{1}\left( g + \frac{m_{1}g - F - \mu m_{2}g}{m_{1} + m_{2}} \right)$

Bài toán 13: (Chuyển động của hệ vật trên hai mặt phẳng nghiêng)

Cho cơ hệ như hình vẽ, Biết m₁, m₂, α, β:

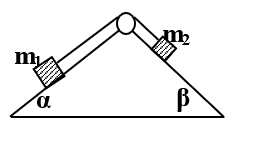
- Bỏ qua ma sát:

Trường hợp 1: m₁gsinα > m₂gsinβ $\Rightarrow$ m₁ đi xuống.

Gia tốc của m₁; m₂ là: $a = \frac{\left( m_{1}\sin\alpha - m_{2}\sin\beta \right)}{m_{1} + m_{2}}g$

Trường hợp 2: m₁gsinα < m₂gsinβ $\Rightarrow$ m₂ đi xuống.

Gia tốc của m₁; m₂ là: $a = \frac{\left( m_{2}\sin\beta - m_{1}\sin\alpha \right)}{m_{1} + m_{2}}g$

- Hệ số ma sat giữa m₁, m₂ với mặt phẳng nghiêng là μ₁, μ₂.

Trường hợp 1: m₁gsinα > m₂gsinβ $\Rightarrow$ m₁ có xu hướng đi xuống., m₂ đi lên,

Gia tốc của m₁; m₂ là: $a = \frac{\left( m_{1}\sin\alpha - m_{2}\sin\beta - \mu_{1}m_{1}cos\alpha - \mu_{2}m_{2}cos\beta \right)}{m_{1} + m_{2}}g$

Trường hợp 2: m₁gsinα < m₂gsinβ $\Rightarrow$ m₁ có xu hướng đi lên., m₂ đi xuống

Gia tốc của m₁; m₂ là: $a = \frac{\left( m_{2}\sin\beta - m_{1}\sin\alpha - \mu_{1}m_{1}cos\alpha - \mu_{2}m_{2}cos\beta \right)}{m_{1} + m_{2}}g$

Bài số 14: Cho cơ hệ như hình vẽ.Cho m₁, m₂ α

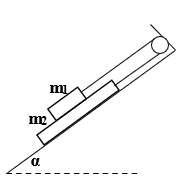
- Bỏ qua mọi ma sát:

Trường hợp 1: m₁ > m₂: Thì m₁ đi xuống m₂ đi lên

Gia tốc của m₁, m₂: $a = \frac{\left( m_{1} - m_{2} \right)\sin\alpha}{m_{1} + m_{2}}.g$

Với a₁ = - a₂ = a

Trường hợp 2: m₁ < m₂: Thì m₁ đi lên, m₂ đi xuống

Gia tốc của m₁, m₂: $a = \frac{\left( m_{2} - m_{1} \right)\sin\alpha}{m_{1} + m_{2}}.g$

Với a₂ = - a₁ = a

- Hệ số ma sát giữa m₂ và sàn μ₁, giữa m₁ và m₂ μ₂

Trường hợp 1: m₁ > m₂: Thì m₁ đi xuống m₂ đi lên

Gia tốc của m₁, m₂:

Ta luôn có a₁ = - a₂ = a. Với a xác định bởi

$a = \frac{\left( m_{1} - m_{2} \right)\sin\alpha - \left( 2\mu_{1} + \mu_{2} \right)cos\alpha}{m_{1} + m_{2}}.g$

Trường hợp 2: m₁ < m₂: Thì m₁ đi lên, m₂ đi xuống

Gia tốc của m₁, m₂: $a = \frac{\left( m_{2} - m_{2} \right)\sin\alpha - \left( 2\mu_{1} + \mu_{2} \right)cos\alpha}{m_{1} + m_{2}}.g$

Với a₂ = - a₁ = a.

📚 Phần tiếp theo của tài liệu đã được tổng hợp trong file đính kèm, mời bạn tải về để đọc tiếp.

-----------------------------------------------------------

Việc nắm vững cách giải các dạng bài tập động lực học Vật lý 10 sẽ giúp học sinh xử lý chính xác bài toán lực và chuyển động, đồng thời tạo nền tảng vững chắc cho các chương tiếp theo. Tài liệu trong bài viết phù hợp cho học sinh tự học, ôn tập và giáo viên tham khảo trong quá trình giảng dạy.

Tải về

Chọn file muốn tải về: