Đề thi thử THPT Quốc gia môn Toán trường THPT Lý Tự Trọng, Hà Tĩnh năm 2015 (Lần 2)

Đề thi thử THPT Quốc gia môn Toán

Nhằm giúp các bạn thi sinh luyện đề THPT Quốc gia môn Toán hiệu quả nhất, VnDoc.com tiếp tục sưu tầm và đăng tải những đề thi chất lượng của các trường THPT Quốc gia trên cả nước để các bạn ôn tập. Mời các bạn tham khảo đề thi thử THPT Quốc gia môn Toán trường THPT Lý Tự Trọng, Hà Tĩnh năm 2015 (Lần 2) với 9 câu hỏi và đáp án đi kèm. Đề thi làm trong thời gian 180 phút.

Tuyển tập 100 hệ phương trình luyện thi đại học

Bộ 10 đề thi thử THPT Quốc gia môn Toán năm 2016

260 bài toán phương trình và hệ phương trình trong ôn thi đại học

Câu 1 (2 điểm). Cho hàm số y = 2x⁴ - 4x² + 2 có đồ thị (C)

a) Khảo sát và vẽ đồ thị (C) của hàm số

b) Viết phương trình tiếp tuyến với đồ thị (C) biết tiếp tuyến có hệ số góc k = 48

Câu 2 (1 điểm).

a) Giải phương trình: √3sin2x + cos2x - 2cosx + 1 = 0

b) Tìm mô đun số phức z biết rằng: và số phức z có phần thực dương

Câu 3 (1 điểm). Tính tích phân sau:

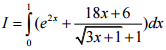
Câu 4 (1 điểm).

a) Tìm hệ số của của số hạng chứa x⁵ trong khai triển nhị thức sau:

b) Giải bất phương trình: log₂ (x - 1) + 2log₄ (x - 2) > log (2x - 4)

Câu 5 (1 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a, SA vuông góc với đáy. Góc tạo bởi SC và mặt phẳng (SAB) bằng 30⁰. Gọi E là trung điểm của BC. Tính thể tích khối chóp S.ABCD và khoảng cách giữa hai đường thẳng DE, SC theo a.

Câu 6 (1 điểm). Trong không gian với hệ toạ độ Oxyz cho A (1;0;1), B(1;2;-3) và mặt phẳng (P): 2x + 2y - z + 1 = 0

a) Viết phương trình của mặt phẳng (Q) đi qua 2 điểm A; B và vuông góc với mặt phẳng (P)

b) Tìm toạ độ điểm M thuộc đường thẳng AB sao cho khoảng cách từ M đến mặt phẳng (P) bằng 2

Câu 7 (1 điểm). Trong mặt phẳng với hệ tọa độ Oxy, cho hình thoi ABCD tâm I, có diện tích bằng 20. Điểm M(0;1/3) thuộc đường thẳng AB, điểm (N0;7) thuộc đường thẳng CD, điểm H(-2;1) thuộc đường cao kẻ từ I của ΔIMN, trọng tâm G của ΔIMN thuộc đường thẳng Δ:x + 3y - 9 = 0. Tìm tọa độ đỉnh B, biết B có hoành độ dương và AC > BD

Câu 8 (1 điểm). Giải hệ phương trình sau:

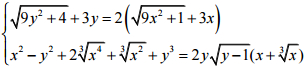
Câu 9 (1 điểm). Cho x, y, z là các số thực thoả mãn: x³ + y³ + z³ - 3xyz = 1. Tìm giá nhỏ nhất của biểu thức: P = x³ + y² + z²

Đáp án đề thi thử THPT Quốc gia môn Toán

Câu 1:

1. a Khảo sát và vẽ đồ thị (C) của hàm số y = 2x⁴ - 4x² + 2

Txđ: D = R

Sự biến thiên: y' = 8x³ - 8x = 8x(x² - 1); y' = 0

→ x = 0; x = 1

Hàm số đồng biến trên các khoảng (-1;0) và (1;+∞)

Hàm số nghịch biến trên các khoảng (-∞;-1) và (0;1)

Hàm số đạt CĐ tại x=0; y_CĐ=2; y_CĐ = 2; Hàm số đạt CT tại x = 1;y_CT = 0

Giới hạn: lim x→±∞ (2x⁴ - 4x² + 2) = +∞

Bảng biến thiên:

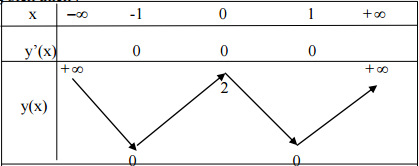
Đồ thị:

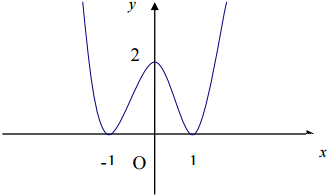
1. b

Gọi M(x₀;y₀) là tiếp điểm ta có: y'(x₀) = 48

8x³₀ - 8x₀ = 48

x³₀ - x₀ - 6 = 0

(x₀ - 2)(x²₀ + 2x₀ + 3) = 0

x₀ = 2

M(2,18)

Vậy phương trình tiếp tuyến là: y = 48x - 78

Câu 2.a

(Còn tiếp)