Giải Toán lớp 5 trang 14 Cánh Diều
Giải Toán 5 trang 14 Bài 4: Ôn tập và bổ sung về phân số Cánh diều gồm hướng dẫn giải chi tiết cho từng hỏi và bài tập, được trình bày khoa học, dễ hiểu giúp các em nắm vững kiến thức được học trong bài. Mời các em tham khảo giải Toán lớp 5 Cánh diều.
Toán lớp 5 trang 14 Cánh diều
Toán lớp 5 tập 1 trang 14 Bài 6
Quy đồng mẫu số hai phân số:
Hướng dẫn giải:
Các bước quy đồng phân số:
- Tìm mẫu số chung
- Tìm thương của mẫu số chung và mẫu số của phân số cần quy đồng
- Nhân cả tử số và mẫu số của phân số với thương vừa tìm được
+) 
\(\frac{3}{4}\) và \(\frac{1}{6}\)
Mẫu số chung: 12
Quy đồng mẫu số 2 phân số:
\(\frac{3}{4} = \frac{{3 \times 3}}{{4 \times 3}}\) = \(\frac{9}{{12}}\) và \(\frac{1}{6} = \frac{{1 \times 2}}{{6 \times 2}} = \frac{2}{{12}}\)
Vậy quy đồng mẫu số hai phân số \(\frac{3}{4}\) và \(\frac{1}{6}\) ta được \(\frac{9}{12}\) và \(\frac{2}{12}\)
+) \(\frac{7}{10}\) và \(\frac{5}{8}\)
Mẫu số chung: 40
Quy đồng mẫu số 2 phân số:
\(\frac{7}{{10}} = \frac{{7 \times 4}}{{10 \times 4}} = \frac{{28}}{{40}}\) và \(\frac{5}{8} = \frac{{5 \times 5}}{{8 \times 5}} = \frac{{25}}{{40}}\)
Vậy quy đồng mẫu số hai phân số \(\frac{7}{10}\) và \(\frac{5}{8}\) ta được \(\frac{28}{40}\) và \(\frac{25}{40}\).
+) \(\frac{4}{9}\)và \(\frac{5}{{16}}\)
Mẫu số chung: 144
Quy đồng mẫu số 2 phân số:
\(\frac{4}{9} = \frac{{4 \times 16}}{{9 \times 16}} = \frac{{64}}{{144}}\) và \(\frac{5}{{16}} = \frac{{5 \times 9}}{{16 \times 9}} = \frac{{45}}{{144}}\)
Vậy quy đồng mẫu số hai phân số \(\frac{4}{9}\)và \(\frac{5}{{16}}\) ta được \(\frac{64}{144}\) và \(\frac{{45}}{{144}}\).
Toán lớp 5 tập 1 trang 14 Bài 7
>, <,= ?
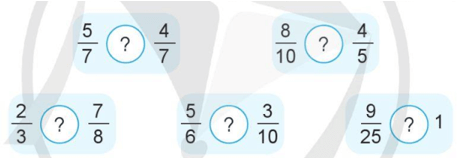
b) Sắp xếp các phân số \(\frac{2}{3}\); \(\frac{6}{7}\); \(\frac{3}{4}\) theo thứ tự từ bé đến lớn.
Hướng dẫn giải:
- Trong hai phân số có cùng mẫu số: Phân số nào có tử số lớn hơn thì lớn hơn.
- Muốn so sánh hai phân số khác mẫu số, ta quy đồng mẫu số hai phân số rồi so sánh hai phân số sau khi quy đồng
a)
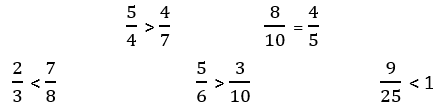
b) Mẫu số chung: 84
Ta có \(\frac{2}{3} = \frac{{2 \times 28}}{{3 \times 28}} = \frac{{56}}{{84}}\)
\(\frac{6}{7} = \frac{{6 \times 12}}{{7 \times 12}} = \frac{{72}}{{84}}\)
\(\frac{3}{4} = \frac{{3 \times 21}}{{4 \times 21}} = \frac{{63}}{{84}}\)
Vì \(\frac{{56}}{{84}} < \frac{{63}}{{84}} < \frac{{72}}{{84}}nên \frac{2}{3} < \frac{3}{4} < \frac{6}{7}.\)
Vậy các phân số đã cho viết theo thứ tự từ bé đến lớn là \(\frac{2}{3}\); \(\frac{3}{4}\);\(\frac{6}{7}\).
Toán lớp 5 tập 1 trang 14 Bài 8
Dung và Đức cùng tham gia trò chơi leo dây với các dây có cùng chiều dài. Dung leo được \(\frac{5}{8}\) sợi dây. Đức leo được \(\frac{4}{10}\) sợi dây.
Theo em:
a) Dung đã leo được sợi dây màu nào? Đức đã leo được sợi dây màu nào?
b) Ai đã leo được đoạn dây dài hơn?
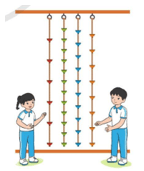
Hướng dẫn giải:
a) Quan sát hình vẽ và đếm số phần trên mỗi sợi dây.
Sợi dây mỗi bạn leo có mẫu số bằng số phần vừa đếm được.
Dung đã leo được sợi dây màu cam, vì sợi dây màu cam được chia làm 8 phần. Đức đã leo được sợi dây màu xanh dương vì sợ dây màu xanh dương được chia làm 10 phần.
b) Mẫu số chung: 40
Quy đồng mẫu số hai phân số:
\(\frac{5}{8} = \frac{{5 \times 5}}{{8 \times 5}} = \frac{{25}}{{40}}; \frac{4}{{10}} = \frac{{4 \times 4}}{{10 \times 4}} = \frac{{16}}{{40}}\)
Vì \(\frac{{25}}{{40}} > \frac{{16}}{{40}}\) nên \(\frac{5}{8} > \frac{4}{{10}}\)
Vậy Dung leo được đoạn dây dài hơn Phúc.
