VnDoc.com

Cách tính độ phóng xạ

Công thức vật lí 12

Bài trước

Tải về

Bài sau

Lớp: Lớp 12

Môn: Vật Lý

Mức độ: Trung bình

Loại File: PDF

Phân loại: Tài liệu Tính phí

Công thức tính độ phóng xạ

A. Độ phóng xạ là gì?
Đơn vị độ phóng xạ
Hằng số phóng xạ
B. Công thức độ phóng xạ
C. Tính độ phóng xạ
D, Bài tập vận dụng tính độ phóng xạ

Vật lý 12 Công thức độ phóng xạ là tài liệu học tập hay, giúp các bạn tổng hợp kiến thức môn Vật lý 12 phần Vật lí hạt nhân một cách nhanh chính xác nhất. Mời quý thầy cô và các bạn cùng tham khảo.

A. Độ phóng xạ là gì?

- Độ phóng xạ đặc trưng cho tính phóng xạ mạnh hay yếu của một lượng chất phóng xạ, kí hiệu là H, có giá bằng số hạt nhân phân rã trong một giây.

Đơn vị độ phóng xạ

Đơn vị của độ phóng xạ là becơren (được lấy theo tên nhà bác học Becquerel), kí hiệu là Bq.

1 Bq = 1 phân rã/1 giây.

Hằng số phóng xạ

Hằng số phóng xạ $\lambda =\frac{\ln2}{T}$ $\lambda =\frac{\ln2}{T}$, đặc trưng cho chất phóng xạ đang xét. Đơn vị của λ là s^-1.

B. Công thức độ phóng xạ

Độ phóng xạ sau khoảng thời gian t là:

$H_{t} = \lambda N_{t} = H_{0}e^{- \lambda t}$ $H_{t} = \lambda N_{t} = H_{0}e^{- \lambda t}$

Trong đó H₀ là độ phóng xạ tại thời điểm ban đầu t = 0.

C. Tính độ phóng xạ

Ví dụ 1. Ban đầu có 5 (g) ²²²Rn là chất phóng xạ với chu kì bán rã T = 3,8 ngày. Tính

a) số nguyên tử có trong 5 (g) Radon.

b) số nguyên tử còn lại sau thời gian 9,5 ngày.

c) độ phóng xạ của lượng Radon nói trên lúc đầu và sau thời gian trên.

Hướng dẫn giải:

a) Ta có số mol của Rn là $n = \frac{m}{A} = \frac{5}{222}$ $n = \frac{m}{A} = \frac{5}{222}$

Khi đó số nguyên tử ban đầu của Rn là

$N_{0} = n.N_{A} = \frac{5}{222}.6,02.10^{23} = 1,356.10^{22}$ $N_{0} = n.N_{A} = \frac{5}{222}.6,02.10^{23} = 1,356.10^{22}$ (nguyên tử)

b) Số nguyên tử còn lại sau 9,5 ngày tính bởi:

$N(t) = N_{0}2^{- \frac{t}{T}} = 1,356.10^{22}.e^{- \frac{ln2}{3,8}.9,5} = 2,93.10^{21}$ $N(t) = N_{0}2^{- \frac{t}{T}} = 1,356.10^{22}.e^{- \frac{ln2}{3,8}.9,5} = 2,93.10^{21}$(nguyên tử)

c) Để tính độ phóng xạ ta cần đổi chu kỳ T ra đơn vị giây.

1 ngày = 24.60.60 (giây)

Độ phóng xạ lúc đầu của Rn:

$H_{0} = \lambda.N_{0} = \frac{ln2}{T}.N_{0} = \frac{0,693.1,356.10^{22}}{3,8.24.60.60} = 2,86.10^{16}(Bq)$ $H_{0} = \lambda.N_{0} = \frac{ln2}{T}.N_{0} = \frac{0,693.1,356.10^{22}}{3,8.24.60.60} = 2,86.10^{16}(Bq)$

Độ phóng xạ sau 9,5 ngày của Rn:

$H = \lambda.N = \frac{ln2}{T}.N = \frac{0,693.2,39.10^{21}}{3,8.24.60.60} = 5,04.10^{15}(Bq)$ $H = \lambda.N = \frac{ln2}{T}.N = \frac{0,693.2,39.10^{21}}{3,8.24.60.60} = 5,04.10^{15}(Bq)$

Ví dụ 2. Chất phóng xạ ²⁵Na có chu kì bán rã T = 62 (s).

a) Tính độ phóng xạ của 0,248 (mg) Na.

b) Tính độ phóng xạ sau 10 phút.

c) Sau bao lâu chất phóng xạ chỉ còn 1/5 độ phóng xạ ban đầu?

Hướng dẫn giải:

a) Số nguyên tử Na ban đầu có trong 0,248 mg Na là $N_{0} = n.N_{A} = \frac{0,248.10^{- 3}}{23}.6,02.10^{23} = 6,49.10^{18}$ $N_{0} = n.N_{A} = \frac{0,248.10^{- 3}}{23}.6,02.10^{23} = 6,49.10^{18}$

Độ phóng xạ tương:

$H_{0} = \lambda.N_{0} = \frac{ln2}{T}.N_{0} = \frac{0,693.6,49.10^{18}}{62} = 7,254.10^{16}(Bq)$ $H_{0} = \lambda.N_{0} = \frac{ln2}{T}.N_{0} = \frac{0,693.6,49.10^{18}}{62} = 7,254.10^{16}(Bq)$

b) Số nguyên tử Na còn lại sau 10 phút là

$N(t) = N_{0}e^{- \lambda t}$ $N(t) = N_{0}e^{- \lambda t}$=6,49.10¹⁸. $= e^{\frac{ln2}{62}.10.60} = 7,94.10^{15}$ $= e^{\frac{ln2}{62}.10.60} = 7,94.10^{15}$ (ng tử)

Độ phóng xạ $H = \lambda.N = \frac{ln2}{T}.N = \frac{0,693.7,94.10^{15}}{10.60}9,17.10^{12}(Bq)$ $H = \lambda.N = \frac{ln2}{T}.N = \frac{0,693.7,94.10^{15}}{10.60}9,17.10^{12}(Bq)$

c) Theo bài ta có

$\frac{H}{H_{0}} = \frac{1}{5} \Leftrightarrow \frac{\lambda N}{\lambda N_{0}} = \frac{1}{5}$ $\frac{H}{H_{0}} = \frac{1}{5} \Leftrightarrow \frac{\lambda N}{\lambda N_{0}} = \frac{1}{5}$ $\Leftrightarrow N = \frac{N_{0}}{5} = N_{0}.e^{- \lambda t} \rightarrow e^{\lambda t} = 5 \Leftrightarrow \lambda t = ln5$ $\Leftrightarrow N = \frac{N_{0}}{5} = N_{0}.e^{- \lambda t} \rightarrow e^{\lambda t} = 5 \Leftrightarrow \lambda t = ln5$

Từ đó ta tìm được $\frac{ln2}{T}.t = ln5 \rightarrow t = \frac{ln5}{ln2}.T = 143,96(s)$ $\frac{ln2}{T}.t = ln5 \rightarrow t = \frac{ln5}{ln2}.T = 143,96(s)$

Ví dụ 3. Rađi $_{88}^{226}\ Ra$ $_{88}^{226}\ Ra$ là nguyên tố phóng xạ α. Một hạt nhân $_{88}^{226}\ Ra$ $_{88}^{226}\ Ra$đang đứng yên phóng ra hạt α và biến đổi thành hạt nhân con X. Biết động năng của hạt α là 4,8 MeV. Lấy khối lượng hạt nhân (tính theo đơn vị amu) bằng số khối của nó. Giả sử phóng xạ này không kèm theo bức xạ gamma. Năng lượng tỏa ra trong phân rã này là bao nhiêu?

Hướng dẫn giải:

$\overrightarrow{P\alpha} = - \overrightarrow{P_{X}}$ $\overrightarrow{P\alpha} = - \overrightarrow{P_{X}}$; về độ lớn $P\alpha = P_{X} \Rightarrow 2m_{\alpha}k_{\alpha} = 2m_{X}k_{X}$ $P\alpha = P_{X} \Rightarrow 2m_{\alpha}k_{\alpha} = 2m_{X}k_{X}$

$= > \frac{k_{\alpha}}{k_{X}} = \frac{m_{X}}{m_{\alpha}} = \frac{u_{X}}{u_{\alpha}} = \frac{222}{4}$ $= > \frac{k_{\alpha}}{k_{X}} = \frac{m_{X}}{m_{\alpha}} = \frac{u_{X}}{u_{\alpha}} = \frac{222}{4}$

=> k_X=0,0864MeV

$\Delta E = k_{\alpha} + k_{X}$ $\Delta E = k_{\alpha} + k_{X}$=4,8864MeV

Ví dụ 4. Hạt nhân $_{88}^{226}\ Ra$ $_{88}^{226}\ Ra$đứng yên phân rã thành hạt α và hạt nhân X (không kèm theo tia γ). Biết năng lượng mà phản ứng tỏa ra là 3,6 MeV và khối lượng của các hạt gần bằng số khối của chúng tính ra đơn vị u. Tính động năng của hạt α và hạt nhân X.

Hướng dẫn giải:

Phương trình phản ứng: $_{88}^{226}\ Ra \rightarrow_{2}^{4}\ \alpha +_{86}^{222}\ Rn$ $_{88}^{226}\ Ra \rightarrow_{2}^{4}\ \alpha +_{86}^{222}\ Rn$

Theo định luật bảo toàn động lượng:

$\overrightarrow{p_{\alpha}} + \overrightarrow{p_{X}} = 0 \Rightarrow p_{\alpha} = m_{\alpha}v_{\alpha} = p_{X} = m_{X}v_{X}$ $\overrightarrow{p_{\alpha}} + \overrightarrow{p_{X}} = 0 \Rightarrow p_{\alpha} = m_{\alpha}v_{\alpha} = p_{X} = m_{X}v_{X}$

$\Rightarrow 2m_{\alpha}K_{\alpha} = 2m_{X}K_{X}$ $\Rightarrow 2m_{\alpha}K_{\alpha} = 2m_{X}K_{X}$

$\Rightarrow K_{X} = \frac{m_{\alpha}}{m_{X}}K_{\alpha}$ $\Rightarrow K_{X} = \frac{m_{\alpha}}{m_{X}}K_{\alpha}$.

Năng lượng tỏa ra trong phản ứng là:

$\Delta E = K_{X} + K_{\alpha} = \frac{m_{\alpha} + m_{X}}{m_{X}}K_{\alpha}$ $\Delta E = K_{X} + K_{\alpha} = \frac{m_{\alpha} + m_{X}}{m_{X}}K_{\alpha}$

$\Rightarrow K_{\alpha} = \frac{m_{X}\Delta E}{m_{\alpha} + m_{X}} = 3,536MeV;$ $\Rightarrow K_{\alpha} = \frac{m_{X}\Delta E}{m_{\alpha} + m_{X}} = 3,536MeV;$ $\Rightarrow K_{X} = \frac{m_{\alpha}}{m_{X}}K_{\alpha} =0,064 MeV$ $\Rightarrow K_{X} = \frac{m_{\alpha}}{m_{X}}K_{\alpha} =0,064 MeV$

Ví dụ 5. Hạt nhân $_{92}^{234}\ U$ $_{92}^{234}\ U$đứng yên phân rã theo phương trình $_{92}^{234}\ U$ $_{92}^{234}\ U$ α + $_{Z}^{A}\ X$ $_{Z}^{A}\ X$. Biết năng lượng tỏa ra trong phản ứng trên là 14,15MeV, động năng của hạt α là bao nhiêu? (lấy xấp xỉ khối lượng các hạt nhân theo đơn vị amu bằng số khối của chúng).

Hướng dẫn giải:

- Bảo toàn năng lượng ta có: Q_tỏa = W_X + W_α = 14,15 (1)

- Bảo toản động lượng ta có: P_α = P_X

⇒ m_αW_α = m_XW_X

⇒ 4W_α - 230W_X = 0 (2)

⇒ từ (1) và (2) ta có: W_α = 13,91 MeV

Ví dụ 6. Cho phản ứng hạt nhân: $_{1}^{3}\ T +_{1}^{2}\ D \rightarrow_{2}^{4}\ He + X + 17,6MeV$ $_{1}^{3}\ T +_{1}^{2}\ D \rightarrow_{2}^{4}\ He + X + 17,6MeV$. Năng lượng toả ra từ phản ứng trên khi tổng hợp được 2g Heli là

A. 52,976.10²³ MeV. B. 5,2976.10²³ MeV.

C. 2,012.10²³ MeV. D. 2,012.10²⁴ MeV.

Hướng dẫn giải

- Số nguyên tử hêli có trong 2g Heli: $N = \frac{m.N_{A}}{A} = \frac{2.6,023.10^{23}}{4} = 3,01.10^{23}$ $N = \frac{m.N_{A}}{A} = \frac{2.6,023.10^{23}}{4} = 3,01.10^{23}$

- Năng lượng toả ra gấp N lần năng lượng của một phản ứng nhiệt hạch:

E = N.Q = 3,01.10²³.17,6 = 52,976.10²³ MeV.

D, Bài tập vận dụng tính độ phóng xạ

Bài tập 1. Bắn hạt $\alpha$ $\alpha$ vào hạt nhân nguyên tử nhôm đang đứng yên gây ra phản ứng: $_{2}^{4}\ He +_{13}^{27}\ Al \rightarrow_{15}^{30}\ P +_{0}^{1}\ n$ $_{2}^{4}\ He +_{13}^{27}\ Al \rightarrow_{15}^{30}\ P +_{0}^{1}\ n$. Biết phản ứng thu năng lượng là 2,70 MeV; giả sử hai hạt tạo thành bay ra với cùng vận tốc và phản ứng không kèm bức xạ $\gamma$ $\gamma$. Lấy khối lượng của các hạt tính theo đơn vị amu có giá trị bằng số khối của chúng. Động năng của hạt $\alpha$ $\alpha$ là

A. 2,70 MeV. B. 3,10 MeV. C. 1,35 MeV. D. 1,55 MeV.

Bài tập 2. Bắn hạt proton có động năng 5,5 MeV vào hạt nhân $_{3}^{7}\ Li$ $_{3}^{7}\ Li$ đang đứng yên gây ra phản ứng hạt hân p + $_{3}^{7}\ Li$ $_{3}^{7}\ Li$ →2α. Giả sử phản ứng không kèm theo bức xạ γ, hai hạt α có cùng động năng và bay theo hai hướng tạo với nhau góc 160⁰. Coi khối lượng của mỗi hạt tính theo đơn vị u gần bằng số khối của nó. Năng lượng mà phản ứng tỏa ra là

A. 14,6 MeV. B. 10,2 MeV. C. 17,3 MeV. D. 20,4 MeV.

Bài tập 3. Chất phóng xạ $_{53}^{131}\ I$ $_{53}^{131}\ I$ dùng trong y tế có chu kỳ bán rã 8 ngày đêm. Nếu nhận được 100 g chất này thì sau 8 tuần lễ khối lượng chất còn lại là

A. 0,87 g. B. 0,78 g. C. 7,8 g. D. 8,7 g.

Bài tập 4. Một chất phóng xạ α có chu kì bán rã T. Khảo sát một mẫu chất phóng xạ này ta thấy: ở lần đo thứ nhất, trong 1 phút mẫu chất phóng xạ này phát ra 8n hạt α. Sau 414 ngày kể từ lần đo thứ nhất, trong 1 phút mẫu chất phóng xạ chỉ phát ra n hạt α. Giá trị của T là

A. 3,8 ngày. B. 138 ngày. C. 12,3 năm. D. 2,6 năm.

Bài tập 5. Dược chất phóng xạ FDG có thành phần là đồng vị $_{9}^{18}\ F$ $_{9}^{18}\ F$ với chu kì bán rã là 110 phút, được sử dụng trong chụp ảnh cắt lớp PET. Dược chất này được sản xuất bằng cách bắn phá vào các hạt đồng vị $_{8}^{18}\ O$ $_{8}^{18}\ O$ nhờ một loại hạt được tăng tốc bằng máy gia tốc. Trước khi chụp ảnh cắp lớp PET, bệnh nhân sẽ được tiêm liều lượng dược chất FDG để đảm bảo độ phóng xạ trên mỗi kg cân nặng là 0,1 mCi không đổi. Hai bệnh nhân cùng cân nặng, cùng sử dụng FDG trong cùng một đợt sản xuất, nhưng được tiêm ở 2 thời điểm cách nhau 60 phút. Bệnh nhân 2 phải tiêm lượng FDG nhiều hơn bệnh nhân 1 bao nhiêu phần trăm? (Kết quả làm tròn đến 3 chữ số có nghĩa).

Đáp án chi tiết bài tập vận dụng

Bài tập 1.

W_tỏa = W = 2,7MeV, v_P = v_n

Hai hạt có cùng vận tốc nên p_P = 30 amu.v; p_n = 1 amu.v ⇒ p_P = 30.p_n

Áp dụng $p^{2} = 2mK$ $p^{2} = 2mK$⇒ 2.30 amu.K_P = 30². 2.1 amu.K_n ⇒ K_P = 30.K_n

ĐLBT động lượng: ${\overrightarrow{p}}_{He} = {\overrightarrow{p}}_{P} + {\overrightarrow{p}}_{n}$ ${\overrightarrow{p}}_{He} = {\overrightarrow{p}}_{P} + {\overrightarrow{p}}_{n}$ vì các vectơ vận tốc cùng chiều nên

$p_{He} = p_{P} + p_{n}$ $p_{He} = p_{P} + p_{n}$= 31.p_n ⇒ 2.4 amu.K_He = 31².2.1u.K_n ⇒ K_He = 240,25.K_n ⇒ K_n = K_He/240,25.

ĐLBT năng lượng: $K_{He} - W = K_{p} + K_{n} = 31.K_{n}$ $K_{He} - W = K_{p} + K_{n} = 31.K_{n}$= 31. K_He/240,25 ⇒ K_He − 31. K_He/240,25 = W

⇒ K_He = $\dfrac{2,7}{1 -\dfrac{31}{240,25}} = 3,1$ $\dfrac{2,7}{1 -\dfrac{31}{240,25}} = 3,1$MeV

Bài tập 2.

Hình vẽ minh họa

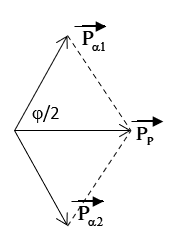
$_{1}^{1}\ H$ $_{1}^{1}\ H$ + $_{3}^{7}\ Li$ $_{3}^{7}\ Li$ → 2 $_{2}^{4}\ He$ $_{2}^{4}\ He$ .

Theo ĐL bảo toàn động lượng

${\overrightarrow{P}}_{p} = {\overrightarrow{P}}_{\alpha 1} + {\overrightarrow{P}}_{\alpha 2}$ ${\overrightarrow{P}}_{p} = {\overrightarrow{P}}_{\alpha 1} + {\overrightarrow{P}}_{\alpha 2}$ P² = 2mK (K là động năng)

cos $\frac{\varphi}{2}$ $\frac{\varphi}{2}$ = $\frac{P_{P}}{2P_{\alpha}}$ $\frac{P_{P}}{2P_{\alpha}}$= $\frac{1}{2}\sqrt{\frac{2m_{P}K_{P}}{2m_{\alpha}K_{\alpha}}}$ $\frac{1}{2}\sqrt{\frac{2m_{P}K_{P}}{2m_{\alpha}K_{\alpha}}}$ = $\frac{1}{2}\sqrt{\frac{m_{P}K_{P}}{m_{\alpha}K_{\alpha}}}$ $\frac{1}{2}\sqrt{\frac{m_{P}K_{P}}{m_{\alpha}K_{\alpha}}}$= $\frac{1}{2}\sqrt{\frac{m_{P}K_{P}}{m_{\alpha}K_{\alpha}}}$ $\frac{1}{2}\sqrt{\frac{m_{P}K_{P}}{m_{\alpha}K_{\alpha}}}$= $\frac{1}{2}\sqrt{\frac{1.K_{P}}{4.K_{\alpha}}}$ $\frac{1}{2}\sqrt{\frac{1.K_{P}}{4.K_{\alpha}}}$

cos $\frac{\varphi}{2}$ $\frac{\varphi}{2}$ = $\frac{1}{4}\sqrt{\frac{K_{P}}{K_{\alpha}}}$ $\frac{1}{4}\sqrt{\frac{K_{P}}{K_{\alpha}}}$ K_α = $\frac{K_{P}}{16cos^{2}80^{0}}$ $\frac{K_{P}}{16cos^{2}80^{0}}$= 2,073K_p = 11,4MeV

Năng lượng mà phản ứng tỏa ra là: ∆E = 2K_α - K_p = 22,8 – 5,5 = 17,3 MeV.

Tài liệu dài, tải về để xem chi tiết và đầy đủ nhé!

---------------------------------------------------------

Trên đây là những kiến thức cơ bản và công thức quan trọng giúp bạn hiểu rõ cách tính độ phóng xạ trong chương trình Vật lí lớp 12. Việc nắm vững công thức và cách áp dụng không chỉ giúp bạn giải quyết tốt các bài tập trong sách giáo khoa mà còn là nền tảng vững chắc cho các kỳ thi quan trọng.

Nếu bạn đang ôn luyện cho kỳ thi THPT Quốc gia hoặc cần củng cố lại kiến thức Vật lí, đừng quên thường xuyên luyện tập và thực hành các dạng bài liên quan đến độ phóng xạ, chu kỳ bán rã và các phương trình đặc trưng. Chúc bạn học tốt và đạt kết quả cao trong học tập!

Tải về

Chọn file muốn tải về: