Chuyển động thẳng biến đổi đều là gì? Công thức, phương trình và bài tập có lời giải
Cách giải bài tập chuyển động biến đổi đều
- A. Chuyển động thẳng biến đổi đều là gì? Ví dụ minh họa thực tế
- B. Phương trình chuyển động thẳng biến đổi đều: Công thức và cách áp dụng
- C. Cách tính quãng đường, vận tốc, gia tốc trong chuyển động thẳng biến đổi đều
- D. Bài tập chuyển động thẳng biến đổi đều từ cơ bản đến nâng cao (có lời giải)
- E. Đáp án bài tập
Chuyển động thẳng biến đổi đều là một trong những chủ đề quan trọng trong chương trình Vật lý lớp 10, xuất hiện thường xuyên trong kiểm tra và đề thi. Vậy chuyển động thẳng biến đổi đều là gì? Bài viết này sẽ giúp bạn hiểu rõ khái niệm, nắm chắc các công thức tính vận tốc, gia tốc, quãng đường, và phương trình chuyển động một cách dễ nhớ. Đặc biệt, bạn sẽ được luyện tập với các bài tập có lời giải chi tiết, giúp nâng cao kỹ năng giải bài và ghi nhớ kiến thức lâu dài.
A. Chuyển động thẳng biến đổi đều là gì? Ví dụ minh họa thực tế
* Chuyển động thẳng biến đổi đều là chuyển động có quỹ đạo là đường thẳng trong đó độ lớn của vận tốc tức thời hoặc tăng đều hoặc giảm đều theo thời gian.
Công thức tính vận tốc
Chọn một chiều dương trên quỹ đạo. Gọi ![]() \(v,v_{0}\)lần lượt là vận tốc tại các thời điểm
\(v,v_{0}\)lần lượt là vận tốc tại các thời điểm ![]() \(t\) và
\(t\) và ![]() \(t_{0}\),
\(t_{0}\), ![]() \(a\) là gia tốc, ta có công thức:
\(a\) là gia tốc, ta có công thức: ![]() \(v = v_{0} + at.\)
\(v = v_{0} + at.\)
- Nếu
 \(a\) cùng dấu với
\(a\) cùng dấu với  \(v\) thì chuyển động là nhanh dần đều.
\(v\) thì chuyển động là nhanh dần đều. - Nếu
 \(a\) trái dấu với
\(a\) trái dấu với  \(v\) thì chuyển động là chậm dần đều.
\(v\) thì chuyển động là chậm dần đều.
Đồ thị vận tốc theo thời gian
Đồ thị của vận tốc theo thời gian ![]() \(t\) là một đường thẳng cắt trục tung tại điểm
\(t\) là một đường thẳng cắt trục tung tại điểm ![]() \(v = v_{0}.\)(Hình 9)
\(v = v_{0}.\)(Hình 9)
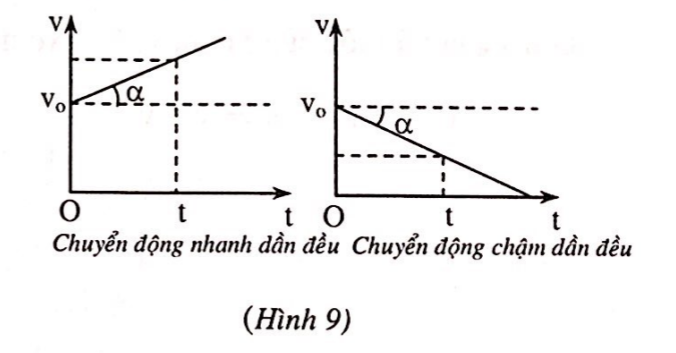
Hệ số góc của đường thẳng đó bằng gia tốc: ![]() \(a = \tan\alpha = \frac{v -
v_{0}}{t}.\)
\(a = \tan\alpha = \frac{v -
v_{0}}{t}.\)
B. Phương trình chuyển động thẳng biến đổi đều: Công thức và cách áp dụng
Phương trình chuyển động
![]() \(x = x_{0} +
v_{0}t + \frac{1}{2}at^{2},\)
\(x = x_{0} +
v_{0}t + \frac{1}{2}at^{2},\)
Trong đó: ![]() \(x_{0}\) và
\(x_{0}\) và ![]() \(v_{0}\) là tọa độ và vận tốc ban đầu,
\(v_{0}\) là tọa độ và vận tốc ban đầu, ![]() \(a\) là gia tốc.
\(a\) là gia tốc.
Nếu ![]() \(x_{0} = 0\) thì phương trình có dạng đơn giản:
\(x_{0} = 0\) thì phương trình có dạng đơn giản: ![]() \(x = v_{0}t +
\frac{1}{2}at^{2}.\)
\(x = v_{0}t +
\frac{1}{2}at^{2}.\)
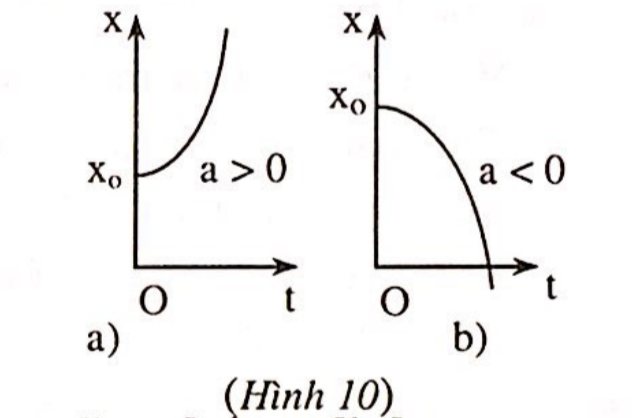
* Đồ thị của tọa độ theo thời gian trong chuyển động thẳng biến đổi đều:
Xét phương trình chuyển động có dạng:
![]() \(x = x_{0} +
\frac{1}{2}at^{2}.\)
\(x = x_{0} +
\frac{1}{2}at^{2}.\)
Đường biểu diễn có phần lõm hướng lên trên
Nếu ![]() \(a > 0\), phần lõm hướng xuống dưới nếu
\(a > 0\), phần lõm hướng xuống dưới nếu ![]() \(a < 0\).
\(a < 0\).
C. Cách tính quãng đường, vận tốc, gia tốc trong chuyển động thẳng biến đổi đều
Kí hiệu ![]() \(s = x - x_{0}\) là quãng đường đi được từ thời điểm 0 đến thời điểm
\(s = x - x_{0}\) là quãng đường đi được từ thời điểm 0 đến thời điểm ![]() \(t,v_{0}\) là vận tốc ban đầu tại thời điểm
\(t,v_{0}\) là vận tốc ban đầu tại thời điểm ![]() \(t = 0,v\) là vận tốc tại thời điểm
\(t = 0,v\) là vận tốc tại thời điểm ![]() \(t,a\) là gia tốc của chuyển động.
\(t,a\) là gia tốc của chuyển động.
Công thức liên hệ: ![]() \(v^{2} - v_{0}^{2} =
2as.\)
\(v^{2} - v_{0}^{2} =
2as.\)
D. Bài tập chuyển động thẳng biến đổi đều từ cơ bản đến nâng cao (có lời giải)
Bài 1. Một chất điểm đang chuyển động thẳng đều với vận tốc 4m/s thì tăng tốc chuyển động nhanh dần đều.
- Tính gia tốc của chất điểm biết rằng sau khi đi được quãng đường 8m thì nó đạt vận tốc 8m/s.
- Viết phương trình chuyển động của chất điểm. Chọn chiều dương là chiều chuyển động, gốc tọa đọ trùng với vị trí chất điểm bắt đầu tăng tốc, gốc thời gian là lúc tăng tốc.
- Xác định vị trí mà tại đó chất điểm có vận tốc 13m/s.
Bài 2. Một đoàn tàu đang chạy với vận tốc 43,2km/h thì hãm phanh, chuyển động thẳng chậm dần đều đề vào ga. Sau 2,5 phút thì tàu dừng lại ở sân ga.
- Tính gia tốc của đoàn tàu.
- Tính quãng đường mà tàu đi được trong thời gian hãm.
Bài 3. Một vật bắt đầu chuyển động thẳng nhanh dần đều với vận tốc ban đầu 6m/s và gia tốc 4m/s2.
- Vẽ đồ thị vận tốc theo thời gian của vật.
- Sau bao lâu vật đạt vận tốc 18m/s. Tính quãng đường vật đi được trong khoảng thời gian đó.
- Viết phương trình chuyển động của vật, từ đó xác định vị trí mà tại đó vận tốc của vật là 12m/s.
Bài 4. Cùng một lúc, từ hai điểm A và B cách nhau 50m có hai vật chuyển động ngược chiều để gặp nhau. Vật thứ nhất xuất phát từ điểm A chuyển động đều với vận tốc 5m/s, vật thứ hai xuất phát từ B chuyển động nhanh dần đều không vận tốc đầu với gia tốc 2m/s2. Chọn trục Ox trùng với đường thẳng AB, gốc O trùng với A, chiều dương từ A đến B, gốc thời gian là lúc xuất phát.
- Viết phương trình chuyển động của mỗi vật.
- Xác định thời điểm và vị trí lúc hai vật gặp nhau.
- Xác định thời điểm mà tại đó hai vật có vận tốc bằng nhau.
Bài 5. Trên hình vẽ là đồ thị vận tốc theo thời gian của một chất điểm chuyển động trên đường thẳng.
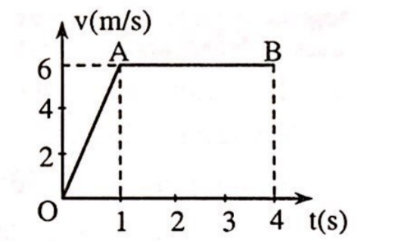
Dựa vào đồ thị, hãy:
- Tính gia tốc của chất điểm trong các giai đoạn
- chuyển động OA và AB.
- Tính quãng đường chất điểm đi được trong 3 giây đầu tiên.
- Tại thời điểm nào, chất điểm có vận tốc 2,4m/s.
E. Đáp án bài tập
Bài 1.
a) Từ công thức ![]() \(v^{2} - v_{0}^{2} =
2as \Rightarrow\) gia tốc:
\(v^{2} - v_{0}^{2} =
2as \Rightarrow\) gia tốc: ![]() \(a =
\frac{v^{2} - v_{0}^{2}}{2s}\)
\(a =
\frac{v^{2} - v_{0}^{2}}{2s}\)
Thay số ta được: ![]() \(a = \frac{8^{2} -
4^{2}}{2.8} = 3\)m/s2.
\(a = \frac{8^{2} -
4^{2}}{2.8} = 3\)m/s2.
b) Phương trình chuyển động có dạng: ![]() \(x =
v_{0}t + \frac{1}{2}at^{2}\).
\(x =
v_{0}t + \frac{1}{2}at^{2}\).
Thay số ta được: ![]() \(x = 4t +
1,5t^{2}\)(m).
\(x = 4t +
1,5t^{2}\)(m).
c) Ta có: ![]() \(v = v_{0} + at \Rightarrow t =
\frac{v - v_{0}}{a} = \frac{13 - 4}{3} = 3\)s.
\(v = v_{0} + at \Rightarrow t =
\frac{v - v_{0}}{a} = \frac{13 - 4}{3} = 3\)s.
Tọa độ của chất điểm lúc đó: ![]() \(x = 4.3 +
1,5.3^{2} = 25,5\)m.
\(x = 4.3 +
1,5.3^{2} = 25,5\)m.
Bài 2.
Chọn chiều dương là chiều chuyển động.
a) Gia tốc: ![]() \(a = \frac{v - v_{0}}{\Delta
t} = \frac{0 - 12}{2,5.60} = - 0,08\)m/s2.
\(a = \frac{v - v_{0}}{\Delta
t} = \frac{0 - 12}{2,5.60} = - 0,08\)m/s2.
b) Từ ![]() \(v^{2} - v_{0}^{2} = 2as
\Rightarrow\) quãng đường tàu đi được trong thời gian hãm:
\(v^{2} - v_{0}^{2} = 2as
\Rightarrow\) quãng đường tàu đi được trong thời gian hãm:
![]() \(s = \frac{v^{2} - v_{0}^{2}}{2a} =
\frac{0 - 12^{2}}{2.( - 0,08)} = 900\)(m).
\(s = \frac{v^{2} - v_{0}^{2}}{2a} =
\frac{0 - 12^{2}}{2.( - 0,08)} = 900\)(m).
Tài liệu dài, tải về để xem chi tiết và đầy đủ nhé!
-------------------------------------------------------------
Qua bài viết trên, hy vọng bạn đã hiểu rõ chuyển động thẳng biến đổi đều là gì, cách áp dụng công thức và phương trình chuyển động vào bài tập thực tế. Đừng quên luyện tập thường xuyên để thành thạo các dạng bài trong đề thi THPT và kiểm tra học kỳ. Nếu thấy bài viết hữu ích, hãy lưu lại và chia sẻ với bạn bè để cùng nhau học tốt Vật lý lớp 10 nhé!









