Đề thi thử vào lớp 10 môn Toán Phòng GD&ĐT Quận 5 năm học 2019 - 2020

Đề thi thử vào lớp 10 môn Toán Phòng GD&ĐT Quận 5 năm 2020

Đề thi thử vào lớp 10 môn Toán Phòng GD&ĐT Quận 5 năm học 2019 - 2020 do thư viện đề thi VnDoc.com sưu tầm. Đây là đề thi tham khảo vào lớp 10 môn Toán dành cho các bạn học sinh ôn tập, củng cố kiến thức, rèn luyện kĩ năng làm bài Toán. Mời các bạn cùng tham khảo

• Đề thi thử vào lớp 10 môn Toán trường THPT Phan Huy Chú, Đống Đa năm học 2017 - 2018
• Đề thi thử vào lớp 10 môn Toán trường THCS Alpha năm học 2017 - 2018 (lần 4)
• Đề thi thử vào lớp 10 môn Toán Sở GD&ĐT Bắc Giang năm học 2019 - 2020
• Đề thi thử vào lớp 10 môn Toán trường THPT chuyên Sư Phạm Hà Nội năm học 2018 - 2019 (lần 2)

Câu 1: (1,5 điểm)

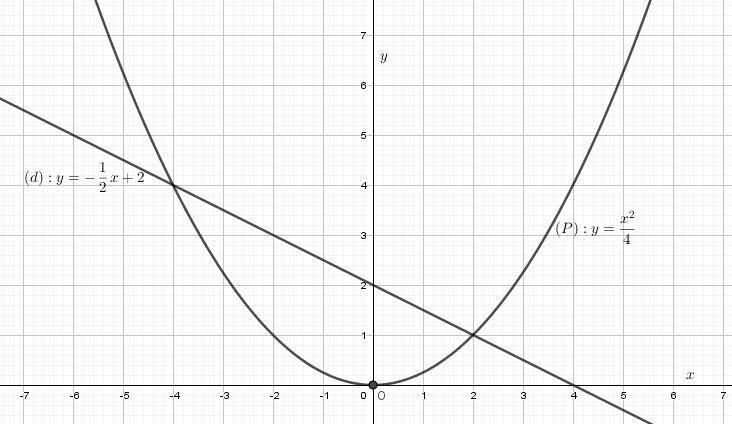
Cho parabol \(\left( P \right):y = \frac{{{x^2}}}{4}\) và đường thẳng \(\left( d \right):y = - \frac{1}{2}x + 2\).

a) Vẽ (P) và (d) trên cùng một hệ trục tọa độ.

b) Tìm tọa độ giao điểm bằng phép tính.

Câu 2: (1 điểm)

Cho phương trình \({x^2} - \left( {2m - 3} \right)x + 2m - 4 = 0\left( 1 \right)\)

Giả sử phương trình (1) có hai nghiệm \(x_1;x_2\). Tìm m để \(\frac{1}{x_1}+\frac{1}{x_2}=\frac{1}{2}\)

Câu 3: (1 điểm)

Giá tiền trứng vịt rẻ hơn trứng gà là 200 đồng/quả, 1 quả trứng vịt có:

Giá 2300 đồng

Trọng lượng trung bình 55g

Tỉ lệ trọng lượng: lòng đỏ 31,9%, lòng trắng 55,8%, vỏ 11,9%, màng vỏ 0,4%.

a) Hỏi 25 quả trứng gà có giá bao nhiêu tiền, biết rằng mua 1 chục trứng gà được bớt 1000 đồng?

b) Hỏi 10 quả trứng vịt khi sử dụng (không tính phần vỏ và màng vỏ) bao nhiêu gram?

Câu 4: (1 điểm)

Giá cước của một công ty taxi như sau: từ 3 km trở xuống là 13 000 đồng, từ hơn 3 km đến 15 km là 15 000 đồng/km, hơn 15 km là 11 000 đồng/km.

a) Hãy biểu thị đại lượng tổng số tiền phải trả y và số km x đi được biết rằng \(3< x \le 15\) dưới dạng hàm số \(y=f(x)\).

b) Tính số km đi được của một hành khách trả số tiền 325 000 đồng?

Câu 5: (1 điểm)

Một chiếc tàu buýt đường sông đưa khách đi xuôi dòng từ bến A đến B, nghỉ 42 phút để đón khách từ bến B về lại bến A, tổng thời gian đi, nghỉ và về là 5 giờ 30 phút. Hãy tìm vận tốc của chiếc tàu buýt đó khi nước yên lặng, biết rằng tốc độ của dòng nước bằng \(\frac{1}{6}\) vận tốc của tàu khi nước đứng yên lặng và khoảng cách giữa A và B là 70 km.

Câu 6: (1 điểm)

Bài toán của Sam Loyd

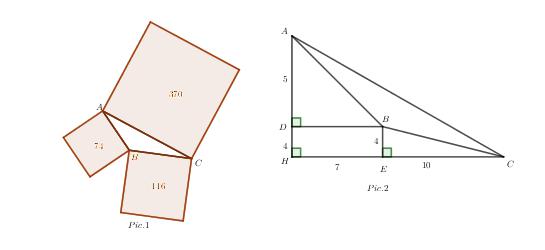
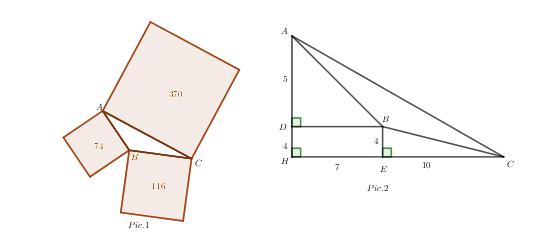
Ở một hội chợ, người ta quảng cáo bán một cái hồ hình tam giác và ba miếng đất hình vuông dựng trên ba cạnh của tam giác đó (hình 1). Diện tích của ba miếng đất đó bằng 74 ac, 116 ac, 370 ac (ac: acre: mẫu Anh, \(3< x \le 15\)). Để tính diện tích tam giác ABC, ta thấy \(74=7^2+5^2\); \(116=10^2+4^2\) và \(370 =9^2+17^2\) nên người ta dựng được hình 2. Hỏi diện tích tam giác ABC bằng bao nhiêu \(m^2\)?

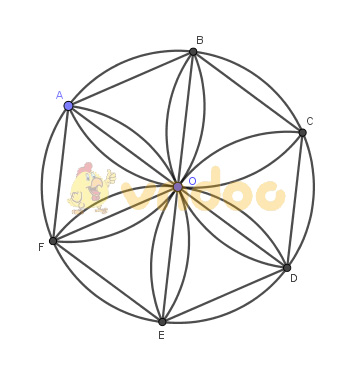
Câu 7: (1 điểm)

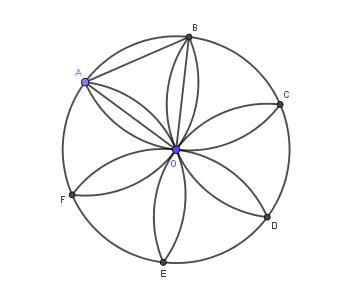
Tính diện tích hình hoa thị 6 cánh tạo bởi 6 cung tròn có bán kính 2 cm và tâm là các đỉnh của lục giác đều nội tiếp đường tròn bán kính 2 cm. (làm tròn đến chữ số thập phân thứ nhất).

Câu 8: (2,5 điểm)

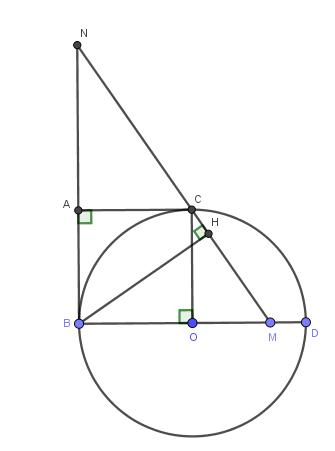
Cho đường tròn (O) đường kính BD = 2R, trên tiếp tuyến tại B của đường tròn (O) lấy điểm A sao cho BA = R. Từ A vẽ tiếp tuyến AC của (O) (C là tiếp điểm và C khác B). Một đường thẳng qua C lần lượt cắt tia BA và BO tại N và M. Vẽ BH vuông góc với MN tại H.

a) Chứng minh OBAC là hình vuông và 5 điểm O, B, A, C, H cùng thuộc một đường tròn.

b) Chứng minh \(AN.OM=R^2\)

c) Tính độ dài đoạn thẳng AN và OM theo R, biết diện tích tam giác MBN bằng \(\frac{9R^2}{4}\)

Gợi ý, hướng dẫn giải và đáp số

Câu 1: (1,5 điểm)

a)

b) Phương trình hoành độ giao điểm của (P) và (d) là:

\({x^2} = - 2x + 8 \Leftrightarrow \left[ \begin{array}{l} x = 2 \Rightarrow y = 2\\ x = - 4 \Rightarrow y = 4 \end{array} \right.\)

Vậy tọa độ giao điểm của hai đồ thị là (2;2) và (-4;4)

Câu 2: (1 điểm)

Ta có:

\(\Delta = {\left( {2m - 3} \right)^2} - 8m + 16 = 4{m^2} - 20m + 25 = {\left( {2m - 5} \right)^2} \ge 0\forall m \in \mathbb{R}\)

Vì vậy, phương trình có 2 nghiệm phân biệt thì \(m \ne \frac{5}{2}\)

Theo định lí Vi ét, ta có: \(\left\{ \begin{array}{l} S = {x_1} + {x_2} = 2m - 3\\ P = {x_1}{x_2} = 2m - 4 \end{array} \right.\)

Ycbt: \(\frac{1}{{{x_1}}} + \frac{1}{{{x_2}}} = \frac{1}{2} \Leftrightarrow \frac{{{x_1} + {x_2}}}{{{x_1}{x_2}}} = \frac{1}{2} \Rightarrow \frac{{2m - 3}}{{2m - 4}} = \frac{1}{2}\) (với \(m \ne 2\))

\(\Leftrightarrow 4m - 6 = 2m - 4 \Leftrightarrow m = 1\left( {t/m} \right)\)

Vậy m = 1 thỏa ycbt.

Câu 3: (1 điểm)

a) Mua 25 quả trứng nên sẽ được giảm 2000 đồng.

Vì vậy số tiền cần mua là: \(25.\left( {2300 + 200} \right) - 2000 = 60\,500\left( {vnd} \right)\)

b) 10 quả trứng vịt khi sử dụng là: \(10.55.\left( {31,9 + 55,8} \right)\% = 482,35\left( g \right)\)

Câu 4: (1 điểm)

a) Hàm số biểu diễn cần tìm là:

\(y = 13000 + 15000\left( {x - 3} \right) = 15000x - 32000\) với \(3< x \le 15\)

b) Giả sử người đó đi đến 15 km thì số tiền cần trả là:

\(15000.15 - 32000=193\,000(vnd)\)

Vì vậy, số tiền khách này cần trả trong đoạn đường tiếp theo là:

\(325\,000 - 193\,000 = 132\,000\left( {vnd} \right)\)

Tương ứng với quãng đường là:

\(132\,000:11 = 12\left( {km} \right)\)

Vì vậy, người khách đã đi \(15+12=27(km)\)

Câu 5: (1 điểm)

Gọi vận tốc lúc nước lặng yên của tàu buýt là x (x >0)

42 phút = 0,7 giờ.

Theo đề, ta có phương trình:

\(\frac{{70}}{{x + \dfrac{x}{6}}} + 0,7 + \frac{{70}}{{x - \dfrac{x}{6}}} = 5,5\)

Giải ra \(x=30(km/h)\)

Câu 6: (1 điểm)

Diện tích tam giác ABC tính theo ac là:

\({S_{ABC}} = \frac{{9.17}}{2} - 4.7 - \frac{{5.7}}{2} - \frac{{4.10}}{2} = 11\left( {ac} \right)\)

Con số này tương đương với: \(44\,517\left( {{m^2}} \right)\)

Câu 7: (1 điểm)

Nối các đoạn thẳng của lục giác đều, ta nhận ra rằng diện tích hoa thị 6 cánh bằng 12 lần diện tích của hình quạt AOB trừ cho diện tích tam giác AOB. Vậy diện tích cần tìm là: \(S = 12.\left( {\frac{{{2^2}.\pi }}{6} - \frac{{2.\sqrt 3 }}{2}} \right) \approx 4,3\left( {c{m^2}} \right)\)

Câu 8: (2,5 điểm)

............................................

Ngoài Đề thi thử vào lớp 10 môn Toán Phòng GD&ĐT Quận 5 năm học 2019 - 2020. Mời các bạn học sinh còn có thể tham khảo các đề thi học kì 2 lớp 9 các môn Toán, Văn, Anh, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với đề Thi vào lớp 10 năm 2019 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn ôn thi tốt