Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

VnDoc.com

Giải bài tập Toán 11 bài 1: Giới hạn của dãy số

Giải Toán 11

Giải bài tập Toán 11 Giải tích: Giới hạn của dãy số

Bài 1 (trang 121 SGK Đại số 11)
Bài 2 (trang 121 SGK Đại số 11)
Bài 3 (trang 121 SGK Đại số 11)
Bài 4 (trang 122 SGK Đại số 11)
Bài 5 (trang 122 SGK Đại số 11)
Bài 6 (trang 122 SGK Đại số 11)
Bài 7 (trang 122 SGK Đại số 11)
Bài 8 (trang 122 SGK Đại số 11)

VnDoc xin giới thiệu tới bạn đọc tài liệu Giải bài tập Toán 11 bài 1: Giới hạn của dãy số, nội dung tài liệu gồm 8 bài tập trang 121, 122 SGK kèm theo lời giải chi tiết sẽ là nguồn thông tin hữu ích để giúp các bạn học sinh có kết quả cao hơn trong học tập. Mời bạn đọc cùng tham khảo chi tiêt và tải về bài viết dưới đây nhé.

Giải bài tập Toán 11 bài 1: Phương pháp quy nạp toán học

Giải bài tập Toán 11 ôn tập chương 3: Dãy số - Cấp số cộng và cấp số nhân

Để tiện trao đổi, chia sẻ kinh nghiệm về giảng dạy và học tập các môn học lớp 11, VnDoc mời các thầy cô giáo, các bậc phụ huynh và các bạn học sinh truy cập nhóm riêng dành cho lớp 11 sau: Nhóm Tài liệu học tập lớp 11. Rất mong nhận được sự ủng hộ của các thầy cô và các bạn.

Giải bài tập Toán 11 Giới hạn của dãy số

Bài 1 (trang 121 SGK Đại số 11)

Có 1kg chất phóng xạ độc hại. Biết rằng cứ sau một khoảng thời gian T = 24000 năm thì một nửa số chất phóng xạ này bị phân rã thành chất khác không độc hại đối với sức khỏe con người (T được gọi chu kỳ bán rã).

Gọi $u_n$ là khối lượng chất phóng xạ còn lại sau chu kỳ thứ n.

a. Tìm số hạng tổng quát u_n của dãy số (u_n)

b. Chứng minh rằng (u_n) có giới hạn là 0.

c. Từ kết quả câu b, chứng tỏ sau một số năm nào đó khối lượng chất phóng xạ đã cho ban đầu không còn độc hại đối với khỏe con người, cho biết chất phóng xạ này sẽ không độc hại nữa nếu khối lượng chất phóng xạ còn lại bé hơn 10^-6 g.

Hướng dẫn giải

Áp dụng kiến thức: $\lim_{x\rightarrow \infty}{q^n}=0$ $\lim_{x\rightarrow \infty}{q^n}=0$ nếu $\left | q \right | <1$ $\left | q \right | <1$

Lời giải:

a. Sau khi bán rã thứ nhất, khối lượng chất phóng xạ là _{${{u}_{1}}=\frac{1}{2}.1=\frac{1}{2}$} kg

Sau chu kì bán rã thứ 2 khối lượng chất phóng xạ là: _{${{u}_{2}}=\frac{1}{2}.\frac{1}{2}=\frac{1}{4}$} kg

…

Sau chu kì bán rã thứ n thì khối lượng chất phóng xạ là: ${{u}_{2}}=\frac{1}{{{2}^{n}}}$ ${{u}_{2}}=\frac{1}{{{2}^{n}}}$ kg

b. $\lim {{u}_{n}}=\lim \frac{1}{{{2}^{n}}}=\lim {{\left( \frac{1}{2} \right)}^{n}}=0$ $\lim {{u}_{n}}=\lim \frac{1}{{{2}^{n}}}=\lim {{\left( \frac{1}{2} \right)}^{n}}=0$ vì _{$0<\frac{1}{2}<1$}

c. Chất phóng xạ không còn độc hại nữa khi khối lượng chất phóng xạ còn lại nhỏ hơn ${{10}^{-6}}g={{10}^{-9}}kg$ ${{10}^{-6}}g={{10}^{-9}}kg$

$\Leftrightarrow {{u}_{n}}<{{10}^{-9}}\Leftrightarrow \frac{1}{{{2}^{n}}}<{{10}^{-9}}\Leftrightarrow {{2}^{n}}>{{10}^{9}}\Leftrightarrow n\ge 30$ $\Leftrightarrow {{u}_{n}}<{{10}^{-9}}\Leftrightarrow \frac{1}{{{2}^{n}}}<{{10}^{-9}}\Leftrightarrow {{2}^{n}}>{{10}^{9}}\Leftrightarrow n\ge 30$

Vậy sau 30 chu kì bằng 30 × 24.000 = 720.000 năm thì chất phóng xạ không còn độc hại.

Bài 2 (trang 121 SGK Đại số 11)

Tìm dãy số $(u_n)$ thảo mãn _{$\left | u_n -1\right |<\dfrac{1}{n^3},\forall n >0$}

Chứng minh rằng: lim u_n= 1

Hướng dẫn giải

Nhắc lại định nghĩa: $\lim u_n=0$ $\lim u_n=0$ nếu có thể nhỏ hơn một số dương bé tùy ý kể từ một số hạng nào đó trở đi

Lời giải:

Cho d > 0 tùy ý:

Ta chọn số tự nhiên ${{n}_{0}}$ ${{n}_{0}}$ sao cho $\frac{1}{{{n}_{0}}^{3}}< d$ $\frac{1}{{{n}_{0}}^{3}}< d$

Ta có: ${{n}_{0}}^{3}>\frac{1}{d}\Leftrightarrow {{n}_{0}}>\sqrt[3]{\frac{1}{d}}$ ${{n}_{0}}^{3}>\frac{1}{d}\Leftrightarrow {{n}_{0}}>\sqrt[3]{\frac{1}{d}}$

Khi đó thì với mỗi số hạng ${{u}_{n}}$ ${{u}_{n}}$ của dãy số $\left( {{u}_{n}} \right)$ $\left( {{u}_{n}} \right)$ mà $n\ge {{n}_{0}}$ $n\ge {{n}_{0}}$ ta đều có

$\left| {{u}_{n}}-1 \right| < \frac{1}{{{n}_{0}}^{3}}< d$ $\left| {{u}_{n}}-1 \right| < \frac{1}{{{n}_{0}}^{3}}< d$

Theo định nghĩa thì $\lim \left( {{u}_{n}}-1 \right)=0$ $\lim \left( {{u}_{n}}-1 \right)=0$ hay $\lim \left( {{u}_{n}} \right)=1$ $\lim \left( {{u}_{n}} \right)=1$

Bài 3 (trang 121 SGK Đại số 11)

Tìm các giới hạn sau:

$\begin{align} & a.\lim \frac{6n-2}{3n+2} \\ & b.\lim \frac{3{{n}^{2}}+n-5}{2{{n}^{2}}+1} \\ & c.\lim \frac{{{3}^{n}}+{{5.4}^{n}}}{{{4}^{n}}+{{2}^{n}}} \\ & d.\lim \frac{\sqrt{9{{n}^{2}}-n+1}}{4n-2} \\ \end{align}$ $\begin{align} & a.\lim \frac{6n-2}{3n+2} \\ & b.\lim \frac{3{{n}^{2}}+n-5}{2{{n}^{2}}+1} \\ & c.\lim \frac{{{3}^{n}}+{{5.4}^{n}}}{{{4}^{n}}+{{2}^{n}}} \\ & d.\lim \frac{\sqrt{9{{n}^{2}}-n+1}}{4n-2} \\ \end{align}$

Hướng dẫn giải

Xem xét bậc cao nhất của tử và mẫu thức. Sau đó chia cả tử và mẫu cho bậc cao nhất của đã xét, hoặc cũng có thể đặt nhân tử cao nhất của cả tử và mẫu để được những giới hạn cơ bản.

Nhận xét: Nếu bậc của tử lớn hơn bậc của mẫu thì giới hạn đó bằng $\pm \infty$ $\pm \infty$

Nếu bậc của tử nhỏ hơn bậc của mẫu thì giới hạn bằng 0.

Nếu bậc của tử bằng bậc của mẫu thì giới hạn đó bằng hệ số bậc cao nhất của tử trên hệ số bậc cao nhất của mẫu.

Ta áp dụng nhận xét này để giải nhanh các bài toán trắc nghiệm.

Lời giải:

$a.\lim \frac{6n-2}{3n+2}=\lim \frac{n\left( 6-\dfrac{1}{n} \right)}{n\left( 3+\dfrac{2}{n} \right)}=\lim \dfrac{6-\dfrac{1}{n}}{3+\dfrac{2}{n}}=\frac{6-0}{3+0}=2$ $a.\lim \frac{6n-2}{3n+2}=\lim \frac{n\left( 6-\dfrac{1}{n} \right)}{n\left( 3+\dfrac{2}{n} \right)}=\lim \dfrac{6-\dfrac{1}{n}}{3+\dfrac{2}{n}}=\frac{6-0}{3+0}=2$

$b.\lim \frac{3{{n}^{2}}+n-5}{2{{n}^{2}}+1}=\lim \dfrac{{{n}^{2}}\left( 3+\dfrac{1}{n}-\dfrac{5}{{{n}^{2}}} \right)}{{{n}^{2}}\left( 2+\dfrac{1}{{{n}^{2}}} \right)}=\lim \dfrac{3+\dfrac{1}{n}-\dfrac{5}{{{n}^{2}}}}{2+\dfrac{1}{{{n}^{2}}}}=\frac{3+0+0}{2+0}=\frac{3}{2}$ $b.\lim \frac{3{{n}^{2}}+n-5}{2{{n}^{2}}+1}=\lim \dfrac{{{n}^{2}}\left( 3+\dfrac{1}{n}-\dfrac{5}{{{n}^{2}}} \right)}{{{n}^{2}}\left( 2+\dfrac{1}{{{n}^{2}}} \right)}=\lim \dfrac{3+\dfrac{1}{n}-\dfrac{5}{{{n}^{2}}}}{2+\dfrac{1}{{{n}^{2}}}}=\frac{3+0+0}{2+0}=\frac{3}{2}$

$\begin{align} & c.\lim \frac{{{3}^{n}}+{{5.4}^{n}}}{{{4}^{n}}+{{2}^{n}}}=\lim \dfrac{{{4}^{n}}\left( \dfrac{{{3}^{n}}}{{{4}^{n}}}+5 \right)}{{{4}^{n}}\left( 1+\dfrac{{{2}^{n}}}{{{4}^{n}}} \right)}=\lim \dfrac{{{\left( \dfrac{3}{4} \right)}^{n}}+5}{1+\dfrac{{{2}^{n}}}{{{4}^{n}}}} \\ & =\dfrac{\lim \left( {{\left( \dfrac{3}{4} \right)}^{n}} \right)+\lim 5}{\lim 1+\lim \left( \dfrac{{{2}^{n}}}{{{4}^{n}}} \right)}=\dfrac{0+5}{1+0}=5 \\ \end{align}$ $\begin{align} & c.\lim \frac{{{3}^{n}}+{{5.4}^{n}}}{{{4}^{n}}+{{2}^{n}}}=\lim \dfrac{{{4}^{n}}\left( \dfrac{{{3}^{n}}}{{{4}^{n}}}+5 \right)}{{{4}^{n}}\left( 1+\dfrac{{{2}^{n}}}{{{4}^{n}}} \right)}=\lim \dfrac{{{\left( \dfrac{3}{4} \right)}^{n}}+5}{1+\dfrac{{{2}^{n}}}{{{4}^{n}}}} \\ & =\dfrac{\lim \left( {{\left( \dfrac{3}{4} \right)}^{n}} \right)+\lim 5}{\lim 1+\lim \left( \dfrac{{{2}^{n}}}{{{4}^{n}}} \right)}=\dfrac{0+5}{1+0}=5 \\ \end{align}$

$d.\lim \frac{\sqrt{9{{n}^{2}}-n+1}}{4n-2}=\lim \dfrac{n\sqrt{9-\dfrac{1}{n}+\dfrac{1}{{{n}^{2}}}}}{n\left( 4-\dfrac{2}{n} \right)}=\frac{\sqrt{9}}{4}=\frac{3}{4}$ $d.\lim \frac{\sqrt{9{{n}^{2}}-n+1}}{4n-2}=\lim \dfrac{n\sqrt{9-\dfrac{1}{n}+\dfrac{1}{{{n}^{2}}}}}{n\left( 4-\dfrac{2}{n} \right)}=\frac{\sqrt{9}}{4}=\frac{3}{4}$

Bài 4 (trang 122 SGK Đại số 11)

Để trang hoàng cho căn hộ của mình, chú chuột mickey quyết định tô màu một miếng bài hình vuông cạnh bằng 1, nó tô màu xám các hình vuông nhỏ được đánh số lần lượt là 1, 2, 3,…, n,…, trong đó cạnh của hình vuông kế tiếp bằng một nửa cạnh hình vuông trước đó. (hình dưới). Giả sử quy trình tô màu của Mickey có thể diễn ra vô hạn.

a. Gọi u_n là diện tích hình vuông màu xám thứ n. Tính u₁, u₂, u₃ và u_n

b. Tính lim S_n với S_n = u₁ + u₂ + u₃ +…+ u_n

Hướng dẫn giải

Số hạng thứ n của cấp số nhân được tính bằng công thức _{$u_n=u_1.q^{n-1}$}trong đó n là số nguyên thỏa mãn $n \ge1$ $n \ge1$

- Công bội khi đó là: _{$q=\left ( \dfrac{u_n}{u_1} \right ) ^{\frac{1}{n-1}}$} hoặc _{$q=\sqrt[n-1]{\dfrac{u_n}{u_1}}$} trong đó n là số nguyên thỏa mãn $n \ge 1$ $n \ge 1$

Áp dụng kiến thức: $\lim_{x\rightarrow \infty}{q^n}=0$ $\lim_{x\rightarrow \infty}{q^n}=0$ nếu $\left | q \right | <1$ $\left | q \right | <1$

Lời giải:

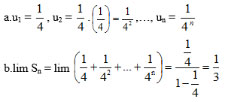
Giải bài tập Toán 11 Giới hạn của dãy số

Bài 5 (trang 122 SGK Đại số 11)

Tính tổng: $S=-1+\frac{1}{10}-\frac{1}{{{10}^{2}}}+...+\frac{{{\left( -1 \right)}^{n}}}{{{10}^{n-1}}}+...$ $S=-1+\frac{1}{10}-\frac{1}{{{10}^{2}}}+...+\frac{{{\left( -1 \right)}^{n}}}{{{10}^{n-1}}}+...$

Hướng dẫn giải

Cấp số nhân vô hạn $(u_n)$ có công bội q với $\left | q \right | <1$ $\left | q \right | <1$ được gọi là cấp số nhân lùi vô hạn và có tổng $S=\dfrac{u_1}{1-q}$ $S=\dfrac{u_1}{1-q}$

Lời giải:

Ta có, dãy số -1; 1/10; 1/10²...; (1-n²)/10^n-1 là một cấp số nhân lùi vô hạn với số hạng đầu u1 = -1 và công bội q = -1/10.

Tổng của cấp số nhân đó là:

Bài 6 (trang 122 SGK Đại số 11)

Cho số thập phân vô hạn tuần hoàn a = 1,020 202…(chu kì là 02). Hãy viết a dưới dạng một phân số:

Hướng dẫn giải

Lời giải:

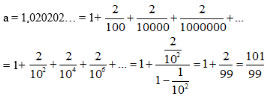
Giải bài tập Toán 11 Giới hạn của dãy số

Bài 7 (trang 122 SGK Đại số 11)

Tính các giới hạn sau:

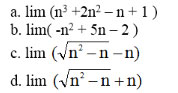
Hướng dẫn giải

Nếu dãy số có chứa căn thức mà không có dạng hữu tỉ để xét bậc ta nhân thêm lượng liên hợp để tính giới hạn.

+ Liên hợp bậc hai: $a^2-b^2=(a-b)(a+b)$

+ Liên hợp bậc 3:

$a^3-b^3=(a-b)(a^2+ab+b^2)$
$a^3+b^3=(a+b)(a^2-ab+b^2)$

Lời giải:

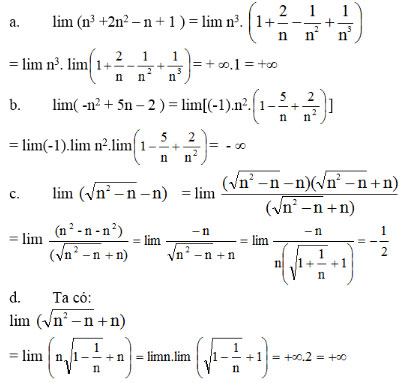
Bài 8 (trang 122 SGK Đại số 11)

Cho hai dãy số (u_n) và (n_n). Biết lim u_n = 3, lim v_n = + ∞. Tính các giới hạn:

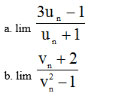
Lời giải:

------------------------------------

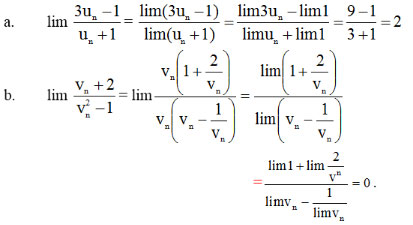
Trên đây VnDoc.com đã giới thiệu tới bạn đọc tài liệu: Giải bài tập Toán 11 bài 1: Giới hạn của dãy số. Chắc hẳn qua bài viết bạn đọc đã nắm được những ý chính cũng như trau dồi được nội dung kiến thức của bài học rồi đúng không ạ? Bài viết được tổng hợp gồm có lời giải chi tiết của các bài tập trong sách giáo khoa môn Toán lớp 11. Hi vọng qua bài viết bạn đọc có thể học tập tốt hơn nhé. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh cùng tham khảo thêm một số tài liệu học tập các môn tại các mục sau Hóa học lớp 11, Giải bài tập Hóa học lớp 11, Hóa học lớp 12, Thi thpt Quốc gia môn Văn, Thi thpt Quốc gia môn Lịch sử, Thi thpt Quốc gia môn Địa lý, Thi thpt Quốc gia môn Toán, đề thi học kì 1 lớp 11, đề thi học kì 2 lớp 11 mà VnDoc tổng hợp và đăng tải.