Lý thuyết Hình học 10 chương 3 bài 1

Lý thuyết hình học 10

Lý thuyết Hình học 10 chương 3 bài 1 được VnDoc biên soạn kỹ lưỡng, khoa học với toàn bộ nội dung trọng tâm của bài học, hỗ trợ quá trình củng cố và tự học của học sinh môn Toán 10 tại nhà.

Hình học 10 - Lý thuyết Phương trình đường thẳng

1. Phương trình tham số

- Vectơ chỉ phương (viết tắt là VTCP) của đường thẳng Δ là vectơ \(\underset{u}{\rightarrow}\) khác vectơ – không và có giá song song hoặc trung với Δ.

- Phương trình tham số của đường thẳng Δ đi qua điểm M₀(x₀; y₀) và có cectơ chỉ phương \(\underset{u}{\rightarrow}\)(a; b) (với a² + b² ≠ 0) là

- Phương trình đường thẳng Δ đi qua điểm M₀(x₀; y₀) và có hệ số góc là k là y = k(x-x₀) + y₀.

- Nếu Δ có vectơ chỉ phương là \(\underset{u}{\rightarrow}\)(a; b) với a ≠ 0 thì hệ số góc của Δ là k = b/a. Ngược lại, nếu Δ có hệ số góc là k thì Δ có vectơ chỉ phương là \(\underset{u}{\rightarrow}\)(1; k).

2. Phương trình tổng quát

- Vectơ pháp tuyến (viết tắt VTPT) của đường thẳng Δ là vectơ \(\underset{n}{\rightarrow}\) khác vectơ – không và vuông góc với vectơ chỉ phương của đường thẳng. Nếu \(\underset{u}{\rightarrow}\)(x; y) là vectơ chỉ phương của đường thẳng thì \(\underset{n}{\rightarrow}\)(-y; x) là vectơ pháp tuyến của đường thẳng đó.

- Phương trình tổng quát của đường thẳng Δ đi qua M₀(x₀; y₀) có vectơ pháp tuyến là \(\underset{n}{\rightarrow}\)(a; b) (với a² + b² ≠0) là: a(x-x₀) + b(y-y₀) = 0

Đường thẳng Δ cắt Ox, Oy tại các điểm khác gốc tọa độ là A(a; 0), B(0; b) có phương trình theo đoạn chắn là

\(\frac{x}{a}+\frac{y}{b}=\ 1\)

3. Vị trí tương đối của hai đường thẳng

- Cho hai đường thẳng d₁: a₁x + b₁y + c₁ = 0 và d₂: a₂x + b₂y + c₂ = 0. Số giao điểm của hai đường thẳng là số nghiệm của hệ phương trình:

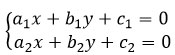
- Hệ vô nghiệm khi và chỉ khi d₁ song song với d₂

- Hệ có nghiệm duy nhất khi và chỉ khi d₁ cắt d₂

- Hệ có vô số nghiệm khi và chỉ khi d₁ trùng d₂

Đặc biệt khi a₂b₂c₂ ≠ 0 thì:

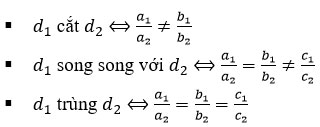
4. Góc giữa hai đường thẳng

- Hai đường thẳng d₁, d₂ lần lượt có vectơ pháp tuyến là \(\underset{n1}{\rightarrow}\) = (a₁; b₁ ), \(\underset{n2}{\rightarrow}\) = (a₂; b₂ ). Khi đó góc của hai đường thẳng được xác định bởi công thức

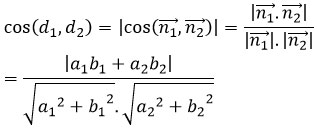
- Nếu đường thẳng d₁,d₂ lần lượt có vectơ chỉ phương \(\underset{u1}{\rightarrow}\), \(\underset{u2}{\rightarrow}\) thì ta cũng có cos⁡(d₁, d₂) = |cos⁡(\(\underset{u1}{\rightarrow}\), \(\underset{u2}{\rightarrow}\))|

- Nếu đường thẳng d₁,d₂ lần lượt có hệ số góc là k₁; k₂ thì ta có

tan(d₁, d₂) = \(\left|\frac{k_1-\ k_2}{1\ +\ k_1k_2}\right|\)

5. Khoản cách từ một điểm đến một đường thẳng

- Khoảng cách từ điểm M₀(x₀; y₀) đến đường thẳng Δ có phương trình tổng quát ax + by + c = 0 là

d (M₀, Δ) = \(\frac{\left|ax_0\ +\ by_0\ +c\right|}{\sqrt{a^2+\ b^2}}\)

- Khoảng cách giữa hai đường thẳng song song d₁: ax + by + c = 0 và d₂: ax + by + d = 0 (trong đó c ≠ d) là

d(d₁, d₂) = \(\frac{\left|c\ -d\right|}{\sqrt{a^2+b^2}}\)

- Đường thẳng Δ có phương trình tổng quát ax + by + c = 0 chia mặt phẳng thành hai nửa mặt phẳng lần lượt xác định bởi ax + byy + c > 0 và ax + by + c < 0.

Phương trinh hai phân giác của các góc tạo bởi hai đường thẳng cắt nhau d₁: a₁x + b₁y + c₁ = 0 và d₂: a₂x + b₂y + c₂ = 0 là

\(\frac{a_1x\ +\ b_1y\ +\ c_1}{\sqrt{a_1^2\ +\ b_1^2}}\ =\pm\frac{a_2x\ +\ b_2y\ +\ c_2}{\sqrt{a_2^2\ \ +b_2^2}}\)