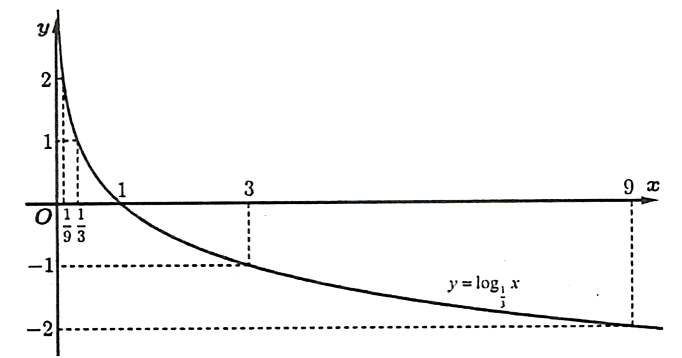
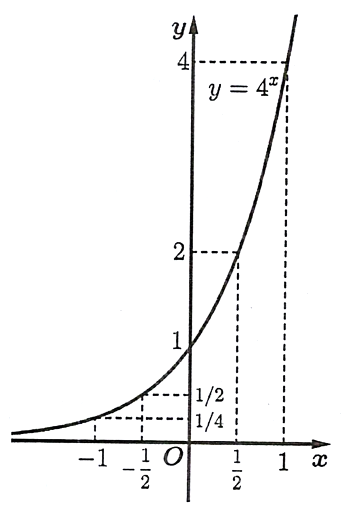
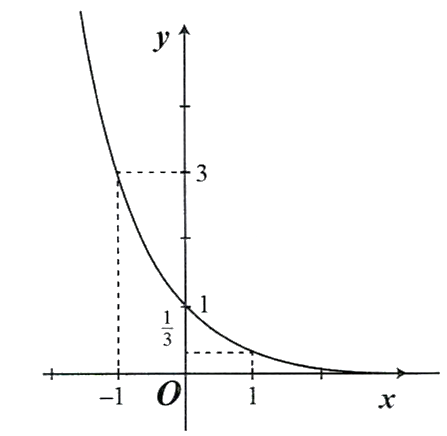
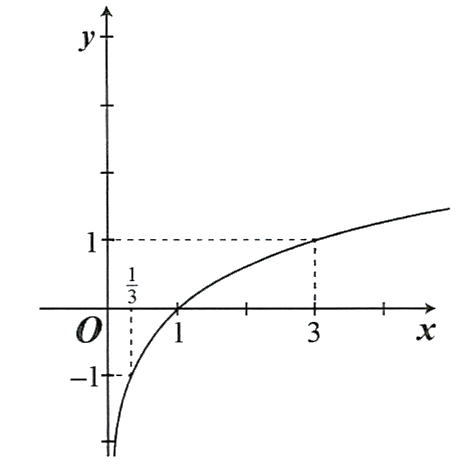
So sánh được các cặp số sau. Khi đó:
a) suy ra
. Đúng||Sai
b) suy ra
. Đúng||Sai
c) suy ra
. Sai||Đúng
d) suy ra
. Sai||Đúng
So sánh được các cặp số sau. Khi đó:
a) suy ra
. Đúng||Sai
b) suy ra
. Đúng||Sai
c) suy ra
. Sai||Đúng
d) suy ra
. Sai||Đúng
|
a) Đúng |
b) Đúng |
c) Sai |
d) Sai |
a) Ta có: suy ra
b) Ta có: suy ra
c) Ta có và
nên hàm số
nghịch biến trên
.
Vậy .
d) Ta có và
nên hàm số
nghịch biến trên
.
Vậy .
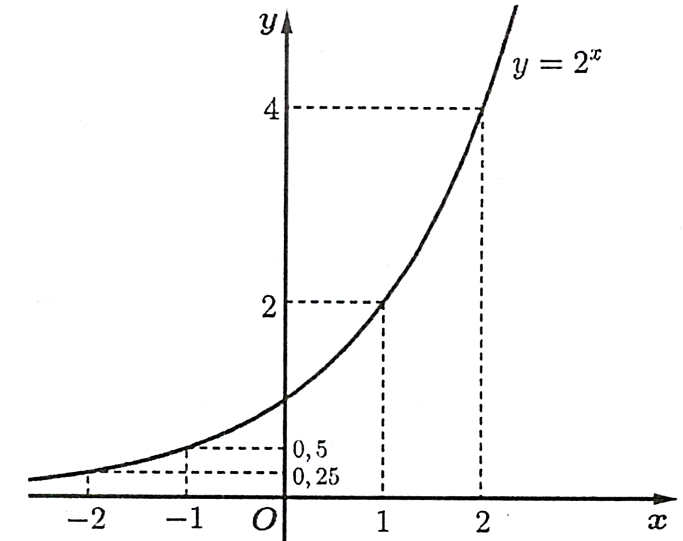 .
.  .
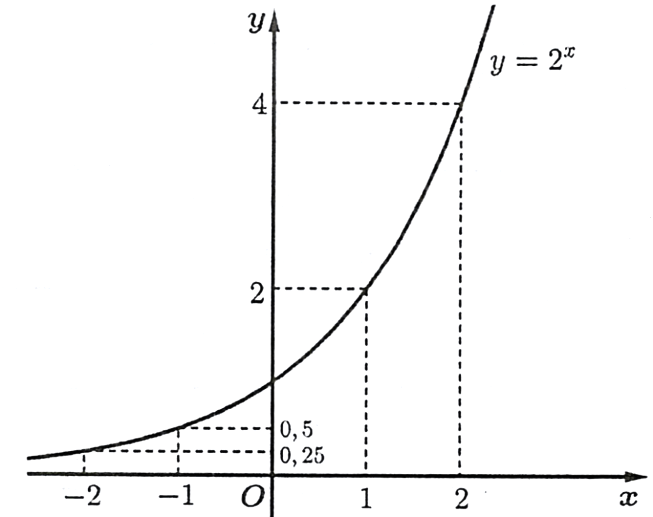
. 

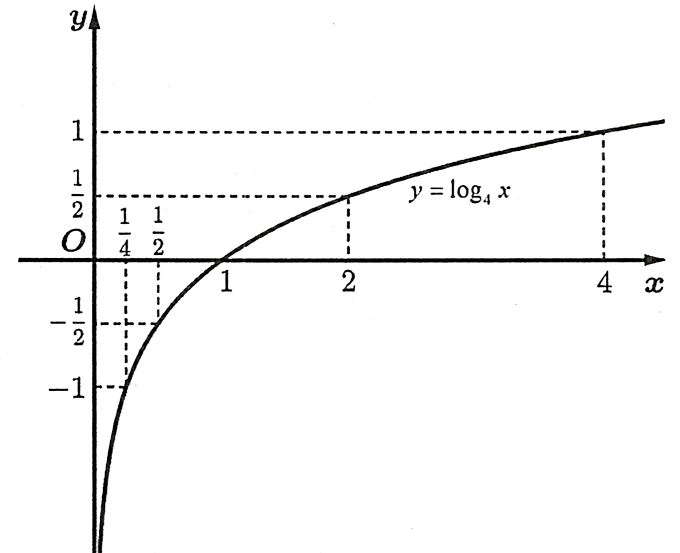

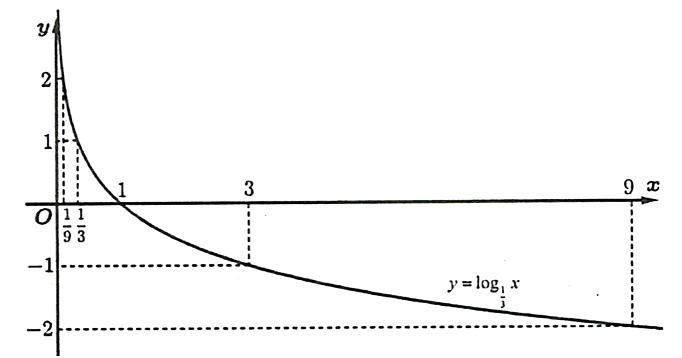 .
. 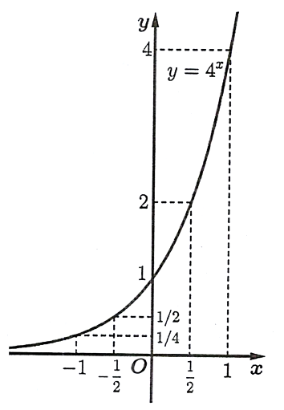 .
. 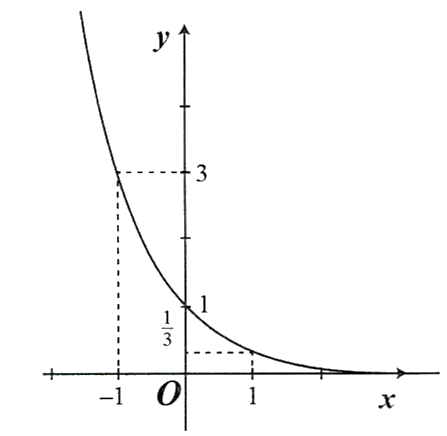 .
. 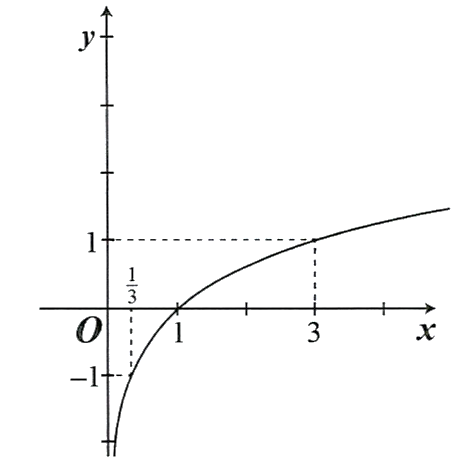 .
.  .
.  .
.  .
.  .
.