VnDoc.com

Hướng dẫn giải bài toán va chạm giữa hai vật Vật lý 10 (dễ hiểu)

Bài tập Vật lý 10 có đáp án

Bài trước

Tải về

Bài sau

Lớp: Lớp 10

Môn: Vật Lý

Dạng tài liệu: Chuyên đề

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Bài toán va chạm giữa hai vật - Có đáp án

A. Cách giải bài toán về va chạm giữa hai vật
B. Bài tập minh họa giải bài toán va chạm

Trong Vật lý 10, bài toán va chạm giữa hai vật là dạng toán quan trọng, thường xuất hiện trong các câu hỏi về động lượng và bảo toàn động lượng. Nếu không nắm rõ quy trình phân tích trước – sau va chạm, học sinh rất dễ nhầm lẫn và mất điểm.

Bài viết Hướng dẫn giải bài toán va chạm giữa hai vật Vật lý 10 (dễ hiểu) trình bày cách làm từng bước, dễ tiếp cận, giúp học sinh lớp 10 hiểu nhanh và áp dụng đúng khi làm bài tập.

A. Cách giải bài toán về va chạm giữa hai vật

Phương pháp giải

Theo định luật bảo toàn động lượng, tổng động lượng trước va chạm bằng tổng động lượng sau va chạm

+ Va chạm đàn hồi : $m_{1}.{\overrightarrow{v}}_{1} + m_{2}.{\overrightarrow{v}}_{2} = m_{1}^{}.{\overrightarrow{v}}_{1}' + m_{2}^{}.{\overrightarrow{v}}_{2}'$

${m_1}.{\vec v_1}$ và ${m_2}.{\vec v_2}$ là động lượng của vật 1 và vật 2 trước tương tác.

$m_1^.\vec v_1'$ và $m_2^.\vec v_2'$ là động lượng của vật 1 và vật 2 sau tương tác.

+ Va chạm mềm : $m_{1}.{\overrightarrow{v}}_{1} + m_{2}.{\overrightarrow{v}}_{2} = (m_{1} + m_{2})\overrightarrow{V}$ $\Rightarrow \overrightarrow{V} = \frac{m_{1}.{\overrightarrow{v}}_{1} + m_{2}.{\overrightarrow{v}}_{2}}{m_{1} + m_{2}}$

+ Chuyển động bằng phản lực $m.\overrightarrow{v} + M.\overrightarrow{V} = \overrightarrow{0} \Rightarrow \overrightarrow{V} = - \frac{m}{M}\overrightarrow{v}$

B. Bài tập minh họa giải bài toán va chạm

Bài 1: Quả cầu I chuyển động trên mặt phẳng ngang trơn, với vận tốc không đổi đến đập vào quả cầu II đang đứng yên. Va chạm là hoàn toàn đàn hồi. Sau va chạm vận tốc hai quả cầu ngược nhau, cùng độ lớn. Tính tỉ số các khối lượng của hai quả cầu.

Hướng dẫn giải

Gọi m₁ và m₂ lần lượt là khối lượng quả cầu I và II; v₀ là vận tốc của quả cầu I trước va chạm; v₁ và v₂ lần lượt là vận tốc của quả cầu I và II sau va chạm.

+ Hai quả cầu đặt trên mặt phẳng ngang nhẵn nên không có lực ma sát, mặt khác trọng lực $\overrightarrow P$ và phản lực $\overrightarrow Q$ cân bằng nhau nên hệ hai quả cầu là hệ kín khi va chạm.

+ Theo định luật bảo toàn động lượng (theo phương ngang), ta có:

m₁v₀ = m₁v₁ + m₂v₂ (1)

- Áp dụng định luật bảo toàn động năng: $\frac{1}{2}m_{1}.{v_{0}}^{2} = \frac{1}{2}m_{1}.{v_{1}}^{2} + \frac{1}{2}m_{2}.{v_{2}}^{2}$ ( 2)

- Sau va chạm vận tốc hai quả cầu ngược chiều nhau, cùng độ lớn nên: v₂ = – v₁ (3)

- Từ (1) và (2): $v_{1} = \frac{(m_{1} - \ m_{2}).v_{0}}{m_{1} + m_{2}};v_{2} = \frac{2.m_{1}.v_{0}}{m_{1} + m_{2}}$

Thay vào (3): m₂=3.m₁ $\Rightarrow \frac{m_{1}}{m_{2}} = \frac{1}{3}$

Bài 2. Quả cầu khối lượng M = 1kg treo ở đầu một dây mảnh nhẹ chiều dài l = 1,5m. Một quả cầu m = 20g bay ngang đến đập vào M với v = 50 m/s. Coi va chạm là đàn hồi xuyên tâm. Tính góc lệch cực đại của dây treo M?

Hướng dẫn giải

Gọi v₁ và v₂ lần lượt là vận tốc của quả cầu m và M ngay sau va chạm.

- Chọn chiều dương theo chiều của vận tốc $\overrightarrow v$ .

Theo phương ngang, động lượng được bảo toàn nên: mv = mv₁ + Mv₂ (1)

- Vì va chạm là đàn hồi xuyên tâm nên động năng bảo toàn:

$\frac{1}{2}m.v^{2} = \frac{1}{2}m.{v_{1}}^{2} + \frac{1}{2}M.{v_{2}}^{2}$ (2)

- Giải hệ ta được: $v_{1} = \frac{(m\ - \ M).v}{m + M};v_{2} = \frac{2.m.v}{m + M}$

- Áp dụng định luật bảo toàn cơ năng cho vật M tại 2 vị trí A và B (gốc thế năng trọng lực tại vị trí cân bằng A): $M.\frac{{v_{2}}^{2}}{2} = M.g.h = M.g.l(1 - cos\alpha)$

$\Rightarrow \cos\alpha = 0,87 \Rightarrow \alpha = 29,5^{0}$

Bài 3. Ba vật khối lượng m₁, m₂, m₃ có thể trượt không ma sát theo một trục nằm ngang (hình vẽ) và m₁, m₃, m₂.

Ban đầu m₁, m₃ đứng yên còn m₂ có vận tốc v. Va chạm là hoàn toàn đàn hồi. Tìm vận tốc cực đại của m₁, m₃ sau đó.

Hướng dẫn giải

Giả sử m₂ va chạm vào m₃ trước (hình vẽ).

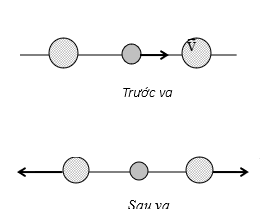
Va chạm giữa m₂ với m₁ và m₃ xảy ra liên tiếp nhiều lần làm cho vận tốc của m₁ và m₃ tăng dần (m₁ dịch chuyển sang trái và m₃ dịch chuyển sang phải), ngược lại vận tốc của m₂ giảm dần.

Quá trình va chạm sẽ kết thúc khi vận tốc cuối cùng v2' của m₂ bắt đầu nhỏ hơn vận tốc của m₁ hoặc m₃. Khi đó vận tốc của m₁ và m₃ đạt cực đại. Gọi các vận tốc cực đại này là v₁ và v₃.

- Áp dụng định luật bảo toàn động lượng cho hệ (chiều dương theo chiều của $\overrightarrow{v}$ ):

$m_{2}v = - m_{1}v_{1} + m_{3}v_{3} + m_{2}v_{2}'$ (1)

- Vì va chạm là hoàn toàn đàn hồi nên cơ năng bảo toàn:

$\frac{1}{2}m_{2}v^{2} = \frac{1}{2}m_{1}v_{1}^{2} + \frac{1}{2}m_{3}v_{3}^{2} + \frac{1}{2}m_{2}{v_{2}'}^{2}$ (2)

- Vì m₁, m₃>>m₂ và $v_{2}'$ < v₁; v₃ nên động lượng cuối cùng $m_{2}v_{2}'$ của m₂ và động năng cuối cùng $\frac{1}{2}m_{2}v_{2}'$ của m₂ là rất nhỏ, có thể bỏ qua so với động năng ban đầu của m₂, động lượng và động năng cuối cùng của m₁ và m₃.

Suy ra: $m_{2}v_{2}' = 0$ ; $\frac{1}{2}m_{2}{v_{2}'}^{2} = 0$ (3)

- Thay (3) vào (1) và (2) ta được: $\left\{ \begin{matrix} \frac{m_{2}}{m_{3}}v = - \frac{m_{1}}{m_{3}}v_{1} + v_{3} \\ \frac{m_{2}}{m_{3}}v^{2} = \frac{m_{1}}{m_{3}}{v_{1}}^{2} + {v_{3}}^{2} \end{matrix} \right.$

- Đặt $b = \frac{m_{2}}{m_{3}};a = \frac{m_{1}}{m_{3}}( \leq 1)$ (4) $\left\{ \begin{matrix} bv = - av_{1} + v_{3}\ \ \ (5) \\ bv^{2} = a{v_{1}}^{2} + {v_{3}}^{2}\ \ \ (6) \end{matrix} \right.$

- Từ (5) suy ra: v₃ = bv + av₁ (7)

- Thay (7) vào (6) ta được: bv² = av₁² + (bv + av₁)²

⇒a(a + 1)v₁² + 2abvv₁ – bv² + b²v² = 0

Vì $b = \frac{m_{2}}{m_{3}} \leq 1$ nên b² 0 ⇒ b²v² $\approx$ 0

⇒ a(a + 1)v₁² + 2abvv₁ – bv² = 0 (8)

- Giải phương trình bậc hai (8) đối với v₁, ta được:

Δ' = (abv)² + ab(a + 1)v² = ab(a + 1)v²; vì (abv)² $\approx$ 0

$v_{1} = \frac{- abv + v\sqrt{ab(a + 1)}}{a(a + 1)} = \frac{- bv}{(a + 1)} + \frac{v\sqrt{ab(a + 1)}}{a(a + 1)}$

Mà $b = \frac{m_{2}}{m_{3}} \leq 1$ nên $\frac{- bv}{(a + 1)} \approx 0$

$\Rightarrow v_{1} \approx \frac{v\sqrt{ab(a + 1)}}{a(a + 1)} = v.\sqrt{\frac{b}{a(a + 1)}}$ (9) (Loại nghiệm v₂ < 0)

- Thay (4) vào (9) ta được : $v_{1} \approx v\sqrt{\frac{m_{1}m_{3}}{m_{1}m_{3} + {m_{1}}^{2}}}$ (10)

- Thay (4) và (10) vào (7) ta được: $v_{3} \approx v\sqrt{\frac{m_{1}m_{3}}{m_{1}m_{3} + {m_{3}}^{2}}}$

Kết luận : Vận tốc cực đại của m₁, m₃ sau đó là

$v_{1} \approx v\sqrt{\frac{m_{1}m_{3}}{m_{1}m_{3} + {m_{1}}^{2}}}$ và $v_{3} \approx v\sqrt{\frac{m_{1}m_{3}}{m_{1}m_{3} + {m_{3}}^{2}}}$

* Chú ý : Nếu m₂ va chạm vào m₁ trước thì ta vẫn có kết quả như trên.

Bài 4. Một búa máy có khối lượng m₁ = 1000kg rơi từ độ cao 3,2m vào một cái cọc có khối lượng m₂ = 100kg. Va chạm là mềm. Lấy g = 10m/s². Tính

a. Vận tốc của búa và cọc sau va chạm.

b. Tỉ số (tính ra phần trăm) giữa nhiệt tỏa ra và động năng của búa.

Hướng dẫn giải

a. Vận tốc của búa trước khi va chạm vào cọc: $v_{1}^{2} = 2gh \Rightarrow v_{1} = \sqrt{2gh} = 8m/s$

Gọi v₂ là vận tốc của búa và cọc ngay sau khi va chạm.

Áp dụng định luật bảo toàn động lượng: $m_{1}v_{1} = (m_{1} + m_{2})v_{2}$

$v_{2} = \frac{m_{1}}{m_{1} + m_{2}}.v_{1} = \frac{1000}{1000 + 100}.8 = 7,3m/s$

b. Va chạm mềm nên động năng của hệ không được bảo toàn. Phần động năng biến thành nhiệt là:

$Q = W_{d1} - W_{d2} = \frac{1}{2}m_{1}v_{1}^{2} - \frac{1}{2}(m_{1} + m_{2})v_{2}^{2}$

Tỉ số giữa nhiệt tỏa ra và động năng của búa: $\frac{Q}{W_{1}} = \frac{2690}{32000}.100\% = 8,4\%$ .

✨ Bài viết chỉ trích dẫn một phần nội dung, mời bạn tải tài liệu đầy đủ để nắm trọn kiến thức.

-------------------------------------------------------

Việc thành thạo cách giải bài toán va chạm giữa hai vật sẽ giúp học sinh xử lý chính xác các bài toán động lượng, đồng thời nâng cao hiệu quả học tập môn Vật lý 10. Bài tập Vật lý 10 có đáp án trong bài viết là tài liệu phù hợp để luyện tập và tự kiểm tra kiến thức.

Xem thử Tải về

Chọn file muốn tải về: