Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

Đóng

Điểm danh hàng ngày

Hôm nay +3
Ngày 2 +3
Ngày 3 +3
Ngày 4 +3
Ngày 5 +3
Ngày 6 +3
Ngày 7 +5

Bạn đã điểm danh Hôm nay và nhận 3 điểm! Đăng nhập ngay để nhận điểm

Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169

VnDoc.com

Bài toán nổ đạn Vật lý 10 theo bảo toàn động lượng

Chuyên đề Vật lý 10 có đáp án

Bài trước

Tải về

Bài sau

Lớp: Lớp 10

Môn: Vật Lý

Dạng tài liệu: Chuyên đề

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Trong Vật lý 10, bài toán nổ đạn là dạng toán điển hình vận dụng định luật bảo toàn động lượng, yêu cầu học sinh phân tích nhanh trạng thái của hệ trước và sau khi nổ. Nếu nắm chắc bản chất và quy trình giải, học sinh có thể xử lý dạng bài này một cách gọn và chính xác.

Bài viết Bài toán nổ đạn Vật lý 10 theo bảo toàn động lượng được xây dựng theo chuyên đề, giúp học sinh nhận diện dạng bài, áp dụng công thức đúng và luyện tập hiệu quả.

A. Phương pháp giải bài toán nổ đạn

Khi một viên đạn nổ thì nội năng là rất lớn nên được coi là một hệ kín

- Theo định luật bảo toàn động lượng $\overrightarrow{p} = {\overrightarrow{p}}_{1} + {\overrightarrow{p}}_{2}$

- Vẽ hình biểu diễn

- Chiếu theo hình biểu diễn xác định độ lớn

B. Bài tập minh họa bài toán nổ đạn

Bài toán 1: Một viên đạn pháo đang bay ngang với vận tốc $v_{0} = 25m/s$ ở độ cao thì nổ, vỡ làm hai mảnh, mảnh 1 có khối lượng $m_{1} = 2,5kg$ , mảnh hai có $m_{2} = 1,5kg$ . Mảnh một bay thẳng đứng xuống dưới và rơi chạm đất với vận tốc $v_{1}' = 90m/s$ . Xác định độ lớn và hướng vận tốc của mảnh thứ hai ngay sau khi đạn nổ. Bỏ qua sức cản của không khí. Lấy $g = 10m/s^{2}$ .

Hướng dẫn giải

Xét hệ gồm hai mảnh. Ngoại lực tác dụng lên hệ là trọng lực $\overrightarrow{P}$ , trọng lực này không đáng kể so với lực tương tác giữa hai mảnh.

Do đó hệ được coi là hệ kín.

Gọi $\overrightarrow{v_{1}}$ , $\overrightarrow{v_{2}}$ lần lượt là vận tốc của mảnh 1 và mảnh 2 ngay sau khi vỡ.

Áp dụng định luật bảo toàn động lượng cho hệ, ta có:

$\left( m_{1} + m_{2} \right)\overrightarrow{v_{0}} = m_{1}\overrightarrow{v_{1}} + m_{2}\overrightarrow{v_{2}}$ (1)

Theo đề bài: $\overrightarrow{v_{1}}$ có chiều thẳng đứng hướng xuống, $\overrightarrow{v_{0}}$ hướng theo phương ngang.

Do đó ta có thể biểu diễn phương trình vectơ (1) như trên hình vẽ.

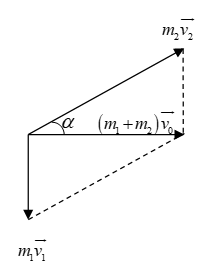
Theo đó:

$m_{2}v_{2} = \sqrt{\left\lbrack \left( m_{1} + m_{2} \right)v_{0} \right\rbrack^{2} + m_{1}^{2}v_{1}^{2}}$ ; $\tan\alpha = \frac{m_{1}v_{1}}{\left( m_{1} + m_{2} \right)v_{0}}$

Để tính vận tốc của mảnh 1 ngay sau khi nổ ta áp dụng công thức: ${v_{1}'}^{2} - v_{1}^{2} = 2gh$

$\Rightarrow v_{1} = \sqrt{{v_{1}'}^{2} - 2gh} = \sqrt{90^{2} - 2.10.80} = 80,62m/s$

Từ (2) ta tính được: $v_{2} = \frac{\sqrt{\left\lbrack \left( m_{1} + m_{2} \right)v_{0} \right\rbrack^{2} + m_{1}^{2}v_{1}^{2}}}{m_{2}} \approx 150m/s$

Từ (3), ta có: $\tan\alpha = 2,015 \Rightarrow \alpha = 64^{0}$ .

Như vậy ngay sau khi viên đạn bị vỡ, mảnh thứ 2 bay theo phương xiên lên trên hợp với phương ngang một góc 64⁰.

Bài toán 2: một mảnh đạn pháo đang bay ngang với vận tốc thì nổ, vỡ thành hai mảnh có khối lượng $m_{1} = 5kg$ và $m_{2} = 15kg$ . Mảnh nhỏ bay lên theo phương thẳng đứng với vận tốc $v_{1} = 400\sqrt{3}m/s$ . Hỏi mảnh to bay theo phương nào, với vận tốc bao nhiêu ? Bỏ qua sức cản không khí.

Hướng dẫn giải

Hệ: hai mảnh đạn là hệ cô lập (nội lực lớn hơn rất nhiều so với ngoại lực)

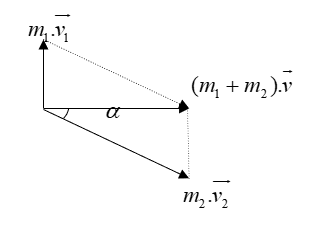
Áp dụng định luật bảo toàn động lượng cho hệ, ta có:

$\left( m_{1} + m_{2} \right)\overrightarrow{v_{0}} = m_{1}\overrightarrow{v_{1}} + m_{2}\overrightarrow{v_{2}}$

$\Rightarrow m_{2}v_{2} = \sqrt{\left\lbrack \left( m_{1} + m_{2} \right)v \right\rbrack^{2} + m_{1}^{2}v_{1}^{2}}$

$\Rightarrow v_{2} = \frac{\sqrt{(m_{1} + m_{2})^{2}.v^{2} + {m_{1}}^{2}.{v_{1}}^{2}}}{m_{2}} \approx 461,88(m/s)$

Với: $\tan\alpha = \frac{m_{1}v_{1}}{\left( m_{1} + m_{2} \right)v} = \frac{\sqrt{3}}{3} \Rightarrow \alpha = 30^{0}$

Bài tập 3: Một viên đạn pháo đang bay ngang với vận tốc 300 (m/s) thì nổ và vỡ thành hai mảnh có khối lượng lần lượt là 15kg và 5kg. Mảnh to bay theo phương thẳng đứng xuống dưới với vận tốc 400 $\sqrt{3}$ (m/s). Hỏi mảnh nhỏ bay theo phương nào với vận tốc bao nhiêu ? Bỏ qua sức cản không khí.

Hướng dẫn giải

Khi đạn nổ lực tác dụng của không khí rất nhỏ so với nội lực nên được coi như là một hệ kín.

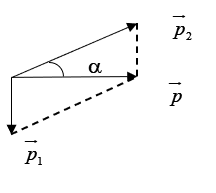
Theo định luật bảo toàn động lượng $\overrightarrow{p} = {\overrightarrow{p}}_{1} + {\overrightarrow{p}}_{2}$

Với

$p_{1} = m_{1}v_{1} = 15.400\sqrt{3} = 6000\sqrt{3}(kgm/s)$

$p_{2} = m_{2}v_{2} = 5.v_{2}(kgm/s)$

Vì ${\overrightarrow{v}}_{1}\bot\overrightarrow{v} \Rightarrow {\overrightarrow{p}}_{1}\bot\overrightarrow{p}$ theo pitago

$p_{2}^{2} = p_{1}^{2} + P^{2} \Rightarrow p_{2} = \sqrt{p_{1}^{2} + p^{2}}$

$\Rightarrow p_{2} = \sqrt{\left( 6000\sqrt{3} \right)^{2} + (6000)^{2}} = 12000(kgm/s)$

$\Rightarrow v_{2} = \frac{p_{2}}{5} = \frac{12000}{5} = 2400(m/s)$

Mà $\sin\alpha = \frac{p_{1}}{p_{2}} = \frac{6000\sqrt{3}}{12000} = \frac{1}{2} \Rightarrow \alpha = 30^{0}$

C. Bài tập vận dụng có hướng dẫn đáp án

Bài tập 1: Cho một viên đạn có khối lượng 2 kg đang bay thẳng đứng lên cao với vận tốc 250 m/s thì nổ thành hai mảnh có khối lượng bằng nhau. Biết mảnh thứ nhất bay theo phương ngang với vận tốc 500 m/s. Hỏi mảnh hai bay thoe phương nào với vận tốc là bao nhiêu. Bỏ qua mọi tac dụng của không khí đối với viên đạn. Lấy g = 10m/s².

Bài tập 2: Một viên đạn được bắn ra khỏi nòng sung ở độ cao 20m đang bay ngang với vận tốc 12,5 m/s thì vỡ thành hai mảnh. Với khối lượng lần lượt là 0,5kg và 0,3kg. Mảnh to rơi theo phương thẳng đứng xuống dưới và có vận tốc khi chạm đất là 40 m/s. Khi đó mảnh hai bay theo phương nào với vận tốc bao nhiêu. Lấy g = 10m/s².

Bài tập 3: Một quả đạn khối lượng m khi bay lên đến điểm cao nhất thì nổ thành hai mảnh. Trong đó một mảnh có khối lượng là $\frac{m}{3}$ bay thẳng đứng xuống dưới với vận tốc 20m/s. Tìm độ cao cực đại mà mảnh còn lại lên tới được so với vị trí đạn nổ. Lấy g = 10m/s².

✨ Bài viết chỉ trích dẫn một phần nội dung, mời bạn tải tài liệu đầy đủ để nắm trọn kiến thức.

-------------------------------------------------------

Việc thành thạo bài toán nổ đạn theo bảo toàn động lượng sẽ giúp học sinh giải nhanh các bài toán cơ học liên quan đến hệ kín, đồng thời củng cố kiến thức trọng tâm của Vật lý 10. Chuyên đề là tài liệu phù hợp để ôn tập, luyện đề và nâng cao kỹ năng giải bài.

Xem thử Tải về

Chọn file muốn tải về: