Lý thuyết Toán 10 Bài 5 KNTT

Giá trị lượng giác của một góc từ 0 độ đến 180 độ

Toán 10 Kết nối tri thức Bài Giá trị lượng giác của một góc từ 0 độ đến 180 độ

1. Giá trị lượng giác của một góc
2. Mối quan hệ giữa các giá trị lượng giác của hai góc bù nhau

Lý thuyết Toán 10 Bài 5 KNTT được VnDoc.com sưu tầm và xin gửi tới bạn đọc cùng tham khảo và có thêm tài liệu học tập nhé.

1. Giá trị lượng giác của một góc

+) Nửa đường tròn đơn vị: nửa đường tròn tâm O, bán kính R = 1 nằm phía trên trục hoành (H.3.2).

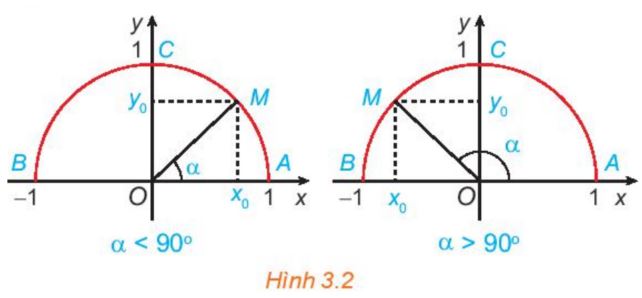
Lý thuyết Toán 10 Bài 5 KNTT

+) Với mỗi góc $\alpha ({0^o} \le \alpha \le {180^o})$ $\alpha ({0^o} \le \alpha \le {180^o})$có duy nhất điểm $M({x_0};{y_0})$ $M({x_0};{y_0})$ trên nửa đường tròn đơn vị nói trên để $\widehat {xOM} = \alpha$ $\widehat {xOM} = \alpha$. Khi đó:

$\sin \alpha = {y_0}$ $\sin \alpha = {y_0}$ là tung độ của M

$\cos \alpha = {x_0}$ $\cos \alpha = {x_0}$ là hoành độ của M

$\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{{{y_0}}}{{{x_0}}}(\alpha \ne {90^o})$ $\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{{{y_0}}}{{{x_0}}}(\alpha \ne {90^o})$

$\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{{{x_0}}}{{{y_0}}}(\alpha \ne {0^o},\alpha \ne {180^o})$ $\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{{{x_0}}}{{{y_0}}}(\alpha \ne {0^o},\alpha \ne {180^o})$

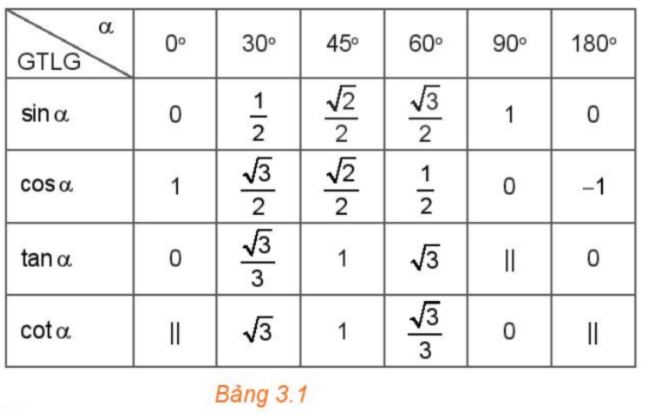
+) Bảng giá trị lượng giác của một số góc đặc biệt:

+) Tìm các giá trị lượng giác của góc bằng máy tính cầm tay.

Trước tiên, bấm phím SHIFT MODE rồi bấm phím 3 để chọn đơn vị góc là “độ”.

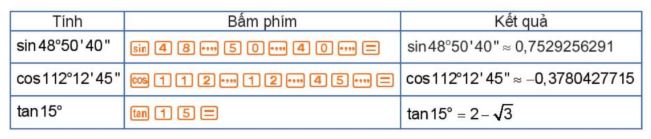
Lý thuyết Toán 10 Bài 5 KNTT

Chú ý:

Khi tìm x biết sin x, mát tính chỉ đưa ra giá trị $x \le {90^o}$ $x \le {90^o}$

Để tính cot x, ta tính 1: tan x.

2. Mối quan hệ giữa các giá trị lượng giác của hai góc bù nhau

* Hai góc bù nhau, $\alpha$ $\alpha$ và ${180^o} - \alpha$ ${180^o} - \alpha$:

$\begin{array}{l}\sin \left( {{{180}^o} - \alpha } \right) = \sin \alpha \\\cos \left( {{{180}^o} - \alpha } \right) = - \cos \alpha \\\tan \left( {{{180}^o} - \alpha } \right) = - \tan \alpha (\alpha \ne {90^o})\\\cot \left( {{{180}^o} - \alpha } \right) = - \cot \alpha ({0^o} < \alpha < {180^o})\end{array}$ $\begin{array}{l}\sin \left( {{{180}^o} - \alpha } \right) = \sin \alpha \\\cos \left( {{{180}^o} - \alpha } \right) = - \cos \alpha \\\tan \left( {{{180}^o} - \alpha } \right) = - \tan \alpha (\alpha \ne {90^o})\\\cot \left( {{{180}^o} - \alpha } \right) = - \cot \alpha ({0^o} < \alpha < {180^o})\end{array}$

* Hai góc phụ nhau, $\alpha$ $\alpha$ và ${90^o} - \alpha$ ${90^o} - \alpha$:

$\begin{array}{l}\sin \left( {{{90}^o} - \alpha } \right) = \cos \alpha \\\cos \left( {{{90}^o} - \alpha } \right) = \sin \alpha \\\tan \left( {{{90}^o} - \alpha } \right) = \cot \alpha (\alpha \ne {90^o},{0^o} < \alpha < {180^o})\\\cot \left( {{{90}^o} - \alpha } \right) = \tan \alpha (\alpha \ne {90^o},{0^o} < \alpha < {180^o})\end{array}$ $\begin{array}{l}\sin \left( {{{90}^o} - \alpha } \right) = \cos \alpha \\\cos \left( {{{90}^o} - \alpha } \right) = \sin \alpha \\\tan \left( {{{90}^o} - \alpha } \right) = \cot \alpha (\alpha \ne {90^o},{0^o} < \alpha < {180^o})\\\cot \left( {{{90}^o} - \alpha } \right) = \tan \alpha (\alpha \ne {90^o},{0^o} < \alpha < {180^o})\end{array}$

VnDoc.com vừa gửi tới bạn đọc bài viết Lý thuyết Toán 10 Bài 5 KNTT. Hi vọng qua bài viết này bạn đọc có thêm tài liệu bổ ích nhé. Mời các bạn cùng tham khảo thêm mục Giải Toán 10 KNTT, Lý thuyết Toán 10 KNTT, Trắc nghiệm Toán 10 KNTT...

Chia sẻ, đánh giá bài viết

1

581

Bài trước

Bài sau