Lý thuyết Toán 10 Bài 25 KNTT

Nhị thức Newton

Toán 10 Kết nối tri thức Bài Nhị thức Newton

VnDoc.com xin gửi tới bạn đọc bài viết Lý thuyết Toán 10 Bài 25 KNTT để bạn đọc cùng tham khảo và có thêm tài liệu học tập nhé. Mời các bạn cùng theo dõi bài viết dưới đây nhé.

Các tích nhận được từ sơ đồ hình cây của một tích các đa thức giống như cách lấy ra một đơn thức từ mỗi đa thức rồi nhân lại với nhau. Hơn nữa, tổng của chúng cho ta khai triển của tích các đa thức đã cho.

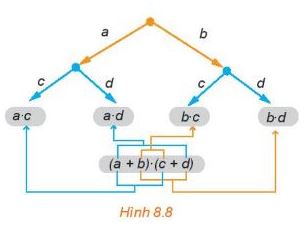
Chẳng hạn, trong sơ đỏ hình cây (H.8.8) của (a + b)(c + d) thì các tích nhận được là a.c, a.d, b.c, b.d cũng chính là các tích nhận được khi ta lấy một hạng tử của nhị thức thứ nhất (là a hoặc b) nhân với một hạng tử của nhị thức thứ hai (là c hoặc d). Ta có

$\left( {a + b} \right).\left( {c + d} \right) = a.c + a.d + b.c + b.d$ $\left( {a + b} \right).\left( {c + d} \right) = a.c + a.d + b.c + b.d$

Lý thuyết Toán 10 Bài 25 KNTT

Ta có công thức sau:

$\begin{array}{l} {\left( {a + b} \right)^4} = {C_4}^0{a^4} + {C_4}^1{a^3}b + {C_4}^2{a^2}{b^2} + {C_4}^3a{b^3} + {C_4}^4{b^4}\\ \;\;\;\;\;\;\;\;\;\;\;\;\; = {a^4} + 4{a^3}b + 6{a^2}{b^2} + 4a{b^3} + {b^4}. \end{array}$ $\begin{array}{l} {\left( {a + b} \right)^4} = {C_4}^0{a^4} + {C_4}^1{a^3}b + {C_4}^2{a^2}{b^2} + {C_4}^3a{b^3} + {C_4}^4{b^4}\\ \;\;\;\;\;\;\;\;\;\;\;\;\; = {a^4} + 4{a^3}b + 6{a^2}{b^2} + 4a{b^3} + {b^4}. \end{array}$

Lý thuyết Toán 10 Bài 25 KNTT

Ví dụ: Khai triển ${\left( {2x + 1} \right)^4}$ ${\left( {2x + 1} \right)^4}$.

Giải

Thay a = 2x và b = 1 trong công thức khai triển của ${\left( {a + b} \right)^4}$ ${\left( {a + b} \right)^4}$, ta được:

$\begin{array}{l} {\left( {2x + 1} \right)^4} = {\left( {2x} \right)^4} + 4.{\left( {2x} \right)^3}.1 + 6.{\left( {2x} \right)^2}{.1^2} + 4.\left( {2x} \right){.1^3} + {1^4}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = 16{x^4} + 32{x^3} + 24{x^2} + 8x + 1 \end{array}$ $\begin{array}{l} {\left( {2x + 1} \right)^4} = {\left( {2x} \right)^4} + 4.{\left( {2x} \right)^3}.1 + 6.{\left( {2x} \right)^2}{.1^2} + 4.\left( {2x} \right){.1^3} + {1^4}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = 16{x^4} + 32{x^3} + 24{x^2} + 8x + 1 \end{array}$

Ta có công thức sau:

$\begin{array}{*{20}{l}} {{{\left( {a + b} \right)}^5} = {C_4}^0{a^5} + {C_5}^1{a^4}b + {C_5}^2{a^3}{b^2} + {C_5}^3{a^2}{b^3} + {C_5}^4a{b^4} + {C_5}^5{b^5}}\\ {\;\;\;\;\;\;\;\;\;\;\;\;\; = {a^5} + 5{a^4}b + 10{a^3}{b^2} + 10{a^2}{b^3} + 5a{b^4} + {b^5}.} \end{array}$ $\begin{array}{*{20}{l}} {{{\left( {a + b} \right)}^5} = {C_4}^0{a^5} + {C_5}^1{a^4}b + {C_5}^2{a^3}{b^2} + {C_5}^3{a^2}{b^3} + {C_5}^4a{b^4} + {C_5}^5{b^5}}\\ {\;\;\;\;\;\;\;\;\;\;\;\;\; = {a^5} + 5{a^4}b + 10{a^3}{b^2} + 10{a^2}{b^3} + 5a{b^4} + {b^5}.} \end{array}$

Lý thuyết Toán 10 Bài 25 KNTT

Ví dụ: Khai triển ${\left( {x + 3} \right)^5}$ ${\left( {x + 3} \right)^5}$.

Giải

Thay a = x và b = 3 trong công thức khai triển của ${\left( {a + b} \right)^5}$ ${\left( {a + b} \right)^5}$, ta được:

$\begin{array}{*{20}{l}} {{{\left( {x + 3} \right)}^5} = {x^5} + 5.{x^4}.3 + 10.{x^3}{{.3}^2} + 10.{x^2}{{.3}^3} + 5.x{{.3}^4} + {3^5}}\\ {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = {x^5} + 15{x^4} + 90{x^3} + 270{x^2} + 405x + 243.} \end{array}$ $\begin{array}{*{20}{l}} {{{\left( {x + 3} \right)}^5} = {x^5} + 5.{x^4}.3 + 10.{x^3}{{.3}^2} + 10.{x^2}{{.3}^3} + 5.x{{.3}^4} + {3^5}}\\ {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = {x^5} + 15{x^4} + 90{x^3} + 270{x^2} + 405x + 243.} \end{array}$

Nhận xét: Các công thức khai triển ${\left( {a + b} \right)^n} với n \in \left\{ {4;5} \right\}$ ${\left( {a + b} \right)^n} với n \in \left\{ {4;5} \right\}$ , là một công cụ hiệu quả để tính chính xác hoặc xấp xỉ một số đại lượng mà không cần dùng máy tính.

Trên đây VnDoc.com vừa gửi tới bạn đọc bài viết Lý thuyết Toán 10 Bài 25 KNTT. Hi vọng qua bài viết này bạn đọc có thêm tài liệu bổ ích. Mời các bạn cùng tham khảo thêm mục Giải Toán 10 KNTT, Lý thuyết Toán 10 KNTT, Trắc nghiệm Toán 10 KNTT...