VnDoc.com

Lý thuyết Toán 10 Bài 11 KNTT

Tích vô hướng của hai Vecto

Bài trước

Tải về

Bài sau

Toán 10 Kết nối tri thức bài Tích vô hướng của hai Vecto

1. Góc giữa hai Vecto
2. Tích vô hướng của hai Vecto
3. Biểu thức tọa độ và tính chất của tích vô hướng

VnDoc.com xin gửi tới bạn đọc bài viết Lý thuyết Toán 10 Bài 11 KNTT để bạn đọc cùng tham khảo. Mời các bạn cùng theo dõi chi tiết.

1. Góc giữa hai Vecto

Cho hai vecto $\overrightarrow u$ $\vec{u}$ và $\overrightarrow v$ $\vec{v}$ khác $\overrightarrow 0$ $\vec{0}$ . Góc giữa hai vecto $\overrightarrow u$ $\vec{u}$ và $\overrightarrow v$ $\vec{v}$ , kí hiệu $\left( {\;\overrightarrow u ,\overrightarrow v } \right)$ $(\vec{u}, \vec{v})$

a) Cách xác định góc: Chọn điểm A bất kì, vẽ $\overrightarrow {AB} = \overrightarrow u$ $\vec{A B} = \vec{u}$ và $\overrightarrow {AC} = \overrightarrow v$ $\vec{A C} = \vec{v}$ . Khi đó $\left( {\;\overrightarrow u ,\overrightarrow v } \right) = \widehat {BAC}.$ $(\vec{u}, \vec{v}) = \hat{B A C} .$

Lý thuyết Toán 10 Bài 11 KNTT

b) Các trường hợp đặc biệt:

+) $\left( {\;\overrightarrow u ,\overrightarrow 0 } \right) = \alpha$ $(\vec{u}, \vec{0}) = α$ tùy ý, với ${0^ \circ } \le \alpha \le {180^ \circ }$ $0^{\circ} \leq α \leq 180^{\circ}$

+) $\left( {\;\overrightarrow u ,\overrightarrow v } \right) = {90^ \circ } \Leftrightarrow \overrightarrow u \bot \overrightarrow v$ $(\vec{u}, \vec{v}) = 90^{\circ} \Leftrightarrow \vec{u} ⊥ \vec{v}$ hoặc $\overrightarrow v \bot \overrightarrow u$ $\vec{v} ⊥ \vec{u}$ . Đặc biệt: $\overrightarrow 0 \bot \overrightarrow u \;\;\forall \overrightarrow u \;$ $\vec{0} ⊥ \vec{u} \forall \vec{u}$

+) $\left( {\;\overrightarrow u ,\overrightarrow v } \right) = {0^ \circ } \Leftrightarrow \overrightarrow u ,\overrightarrow v$ $(\vec{u}, \vec{v}) = 0^{\circ} \Leftrightarrow \vec{u}, \vec{v}$ cùng hướng

+) $\left( {\;\overrightarrow u ,\overrightarrow v } \right) = {180^ \circ } \Leftrightarrow \overrightarrow u ,\overrightarrow v$ $(\vec{u}, \vec{v}) = 180^{\circ} \Leftrightarrow \vec{u}, \vec{v}$ ngược hướng

2. Tích vô hướng của hai Vecto

+) Tích vô hướng của hai vecto $\overrightarrow u ,\;\overrightarrow v : \overrightarrow u .\;\overrightarrow v = \left| {\overrightarrow u } \right|.\;\left| {\overrightarrow v } \right|.\cos \;\left( {\overrightarrow u ,\;\overrightarrow v } \right)$ $\vec{u}, \vec{v} : \vec{u} . \vec{v} = | \vec{u} | . | \vec{v} | . \cos (\vec{u}, \vec{v})$

+) $\overrightarrow u .\;\overrightarrow v \;\; = 0 \Leftrightarrow \overrightarrow u \bot \;\overrightarrow v \;\;$ $\vec{u} . \vec{v} = 0 \Leftrightarrow \vec{u} ⊥ \vec{v}$

+) $\overrightarrow u .\;\overrightarrow u \;\; = {\overrightarrow u ^2} = \left| {\overrightarrow u } \right|.\left| {\overrightarrow u } \right|.\cos {0^ \circ } = {\left| {\overrightarrow u } \right|^2}$ $\vec{u} . \vec{u} = {\vec{u}}^{2} = | \vec{u} | . | \vec{u} | . \cos 0^{\circ} = {| \vec{u} |}^{2}$

3. Biểu thức tọa độ và tính chất của tích vô hướng

a) Biểu thức tọa độ của tích vô hướng

Cho $\overrightarrow u (x;y)$ $\vec{u} (x; y)$ và $\overrightarrow v = (x$ $\vec{v} = (x^{'}; y^{'}) .$

Khi đó $\overrightarrow u .\;\overrightarrow v \;\; = xx$ $\vec{u} . \vec{v} = x x^{'} + y y^{'}$

Hệ quả:

+) $\overrightarrow u \bot \;\overrightarrow v \; \Leftrightarrow xx$ $\vec{u} ⊥ \vec{v} \Leftrightarrow x x^{'} + y y^{'} = 0$

+) ${\overrightarrow u ^2} = \overrightarrow u .\;\overrightarrow u \;\; = x.x + y.y = {x^2} + {y^2}$ ${\vec{u}}^{2} = \vec{u} . \vec{u} = x . x + y . y = x^{2} + y^{2}$

+) Tìm góc giữa hai vecto: $\cos \left( {\;\overrightarrow u ,\overrightarrow v } \right) = \frac{{\;\overrightarrow u .\overrightarrow v }}{{\;\left| {\overrightarrow u } \right|.\left| {\overrightarrow v } \right|}} = \frac{{xx$ $\cos (\vec{u}, \vec{v}) = \frac{\vec{u} . \vec{v}}{| \vec{u} | . | \vec{v} |} = \frac{x x^{'} + y y^{'}}{\sqrt{x^{2} + y^{2}} . \sqrt{x^{' 2} + y^{' 2}}}$

b) Công thức tính tích vô hướng khi biết độ dài:

Theo định lí cosin: $\cos \widehat {BAC} = \frac{{A{B^2} + A{C^2} - B{C^2}}}{{2.AB.AC}}$ $\cos \hat{B A C} = \frac{A B^{2} + A C^{2} - B C^{2}}{2. A B . A C}$

$\Rightarrow \overrightarrow {AB} .\overrightarrow {AC} = AB.AC.\cos \widehat {BAC} = A{B^2} + A{C^2} - B{C^2}$ $\Rightarrow \vec{A B} . \vec{A C} = A B . A C . \cos \hat{B A C} = A B^{2} + A C^{2} - B C^{2}$

c) Tính chất

Cho 3 vecto $\overrightarrow u ,\overrightarrow v ,\overrightarrow w$ $\vec{u}, \vec{v}, \vec{w}$ bất kì và mọi số thực k, ta có:

$\begin{array}{l}\overrightarrow u .\;\overrightarrow v \;\; = \overrightarrow v .\;\overrightarrow u \;\\\overrightarrow u .\;\left( {\overrightarrow v + \overrightarrow w \;} \right)\; = \overrightarrow u .\;\overrightarrow v \; + \overrightarrow u .\;\overrightarrow w \;\\\left( {k\overrightarrow u } \right).\overrightarrow v = k.\left( {\overrightarrow u .\;\overrightarrow v \;} \right) = \overrightarrow u .\;\left( {k\overrightarrow v \;} \right)\end{array}$ $\begin{array}{l} \vec{u} . \vec{v} = \vec{v} . \vec{u} \\ \vec{u} . (\vec{v} + \vec{w}) = \vec{u} . \vec{v} + \vec{u} . \vec{w} \\ (k \vec{u}) . \vec{v} = k . (\vec{u} . \vec{v}) = \vec{u} . (k \vec{v}) \end{array}$

Hệ quả

$\begin{array}{l}\overrightarrow u .\;\left( {\overrightarrow v - \overrightarrow w \;} \right)\; = \overrightarrow u .\;\overrightarrow v \; - \overrightarrow u .\;\overrightarrow w \\{\left( {\overrightarrow u + \overrightarrow v } \right)^2}\;\; = {\overrightarrow u ^2} + 2\overrightarrow u .\;\overrightarrow v \; + \;{\overrightarrow v ^2};\;\;{\left( {\overrightarrow u - \overrightarrow v } \right)^2}\;\; = {\overrightarrow u ^2} - 2\overrightarrow u .\;\overrightarrow v \; + \;{\overrightarrow v ^2}\\\left( {\overrightarrow u + \overrightarrow v } \right)\left( {\overrightarrow u - \overrightarrow v } \right) = {\overrightarrow u ^2} - {\overrightarrow v ^2}\end{array}$ $\begin{array}{l} \vec{u} . (\vec{v} - \vec{w}) = \vec{u} . \vec{v} - \vec{u} . \vec{w} \\ {(\vec{u} + \vec{v})}^{2} = {\vec{u}}^{2} + 2 \vec{u} . \vec{v} + {\vec{v}}^{2}; {(\vec{u} - \vec{v})}^{2} = {\vec{u}}^{2} - 2 \vec{u} . \vec{v} + {\vec{v}}^{2} \\ (\vec{u} + \vec{v}) (\vec{u} - \vec{v}) = {\vec{u}}^{2} - {\vec{v}}^{2} \end{array}$

Sơ đồ tư duy - Tích vô hướng của hai Vecto

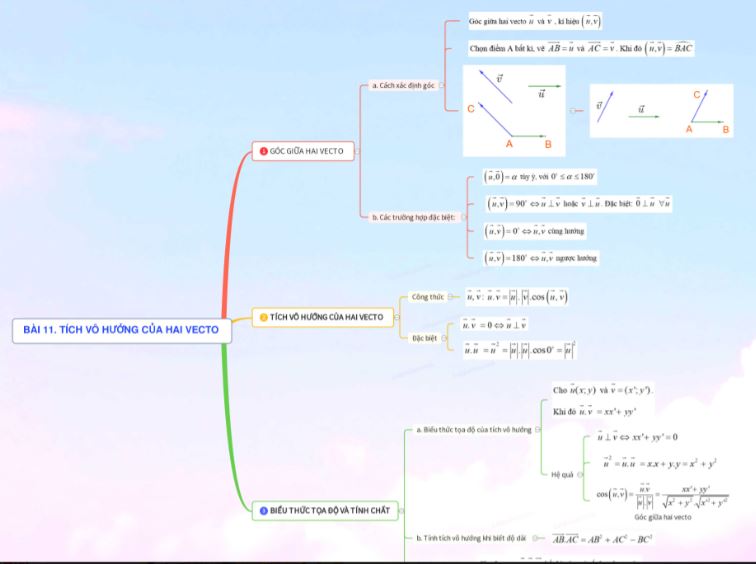
Lý thuyết Toán 10 Bài 11 KNTT

VnDoc.com vừa gửi tới bạn đọc bài viết Lý thuyết Toán 10 Bài 11 KNTT. Bài viết đã giới thiệu tới bạn đọc nội dung lý thuyết về Toán 10 KNTT. Mời các bạn cùng tham khảo thêm mục Giải Toán 10 KNTT, Lý thuyết Toán 10 KNTT, Trắc nghiệm Toán 10 KNTT...

Lý thuyết Toán 10 Bài 12 KNTT

Chia sẻ, đánh giá bài viết

1

287

Bài trước

Bài sau

Chia sẻ bởi:
Nguyễn Linh An

Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này!

Đóng

79.000 / tháng

Mua ngay

Đặc quyền các gói Thành viên

PRO

Phổ biến nhất

PRO+

Tải tài liệu Cao cấp 1 Lớp

Tải tài liệu Trả phí + Miễn phí

Xem nội dung bài viết

Trải nghiệm Không quảng cáo

Làm bài trắc nghiệm không giới hạn

Tìm hiểu thêm

Mua cả năm Tiết kiệm tới 48%

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!