Lý thuyết Toán 10 Bài 7 KNTT

+) Vecto là một đoạn thẳng có hướng.

Ví dụ 1: i) vecto $\overrightarrow{AB}$: (đọc là vecto AB)

ii) Vecto $\overrightarrow{BA}$:

iii) vecto $\overrightarrow{u}$: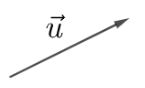

+) Độ dài của vecto là khoảng cách giữa điểm đầu và điểm cuối của vecto đó.

Kí hiệu: độ dài của vecto $\overrightarrow{AB}$ là $\left|\overrightarrow{AB}\right|.$

Ví dụ 2: $\left|\overrightarrow{AB}\right|=AB;\left|\overrightarrow{DE}\right|=DE$

+) Vecto không, là vecto có độ dài bằng 0. Ví dụ: $\overrightarrow{AA},\overrightarrow{EE},...$(điểm đầu trùng điểm cuối)

Kí hiệu chung là $\overrightarrow{0}$.

2. Hai Vectơ cùng phương, cùng hướng, bằng nhau

+) Giá của vecto: là đường thẳng đi qua điểm đầu và điểm cuối của vecto đó.

Ví dụ: Giá của vecto $\overrightarrow{CD}$ là đường thẳng CD

+) Hai vecto được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.

+) Hai vecto cùng phương thì chúng cùng hướng hoặc ngược hướng.

Ví dụ:

Ba vecto $\overrightarrow{u},\overrightarrow{CD},\overrightarrow{AB}$cùng phương.

Trong đó 2 vecto $\overrightarrow{u},\overrightarrow{CD}$cùng hướng, còn 2 vecto $\overrightarrow{CD},\overrightarrow{AB}$ngược hướng.

+) Hai vecto được gọi là bằng nhau nếu chúng có cùng độ dài và cùng hướng.

* Chú ý:

- Chỉ khi hai vecto cùng phương ta mới nói tới chúng cùng hướng hay ngược hướng.

- Vecto $\overrightarrow{0}$cùng phương, cùng hướng với mọi vecto.

- Với mỗi điểm O và vecto $\overrightarrow{a}$cho trước, có duy nhất điểm A sao cho $\overrightarrow{OA}=\overrightarrow{a}$

* Nhận xét:

+) Ba điểm A, B, C thẳng hàng khi và chỉ khi $\overrightarrow{AB}$ và $\overrightarrow{AC}$ cùng phương.

+) Ba điểm A, B, C thẳng hàng, B nằm giữa khi và chỉ khi $\overrightarrow{AB}$ và $\overrightarrow{AC}$cùng hướng.