Sơ đồ tư duy Hình học 8 chương 1
Sơ đồ tư duy Hình học 8 chương 1 được VnDoc sưu tầm và đăng tải giúp các em nắm bắt các kiến thức cơ bản một cách nhanh nhất. Từ đó giúp các em có một nền tảng kiến thức vững chắc để phát triển tư duy và trí tuệ vận dụng tốt để giải các bài tập Toán 8 và các lớp cao hơn. Dưới đây là nội dung chi tiết các em tham khảo nhé
Sơ đồ tư duy Hình học 8
Tóm tắt lý thuyết chương I: Tứ giác
1. Tứ giác
a) Định nghĩa
Tứ giác ABCD là hình gồm bốn đoạn thẳng AB, BC, CD, DA trong đó bất kì đoạn thẳng nào cũng không cùng nằm trên một đường thẳng.
b) Tổng các góc của tứ giác
Định lí: Tổng các góc của một tứ giác bằng 3600.
2. Hình thang
a) Định nghĩa
Hình thang là tứ giác có hai cạnh đối song song.
+ Hai cạnh song song gọi là hai đáy.
+ Hai cạnh còn lại gọi là hai cạnh bên.
b) Hình thang vuông
Định nghĩa: Hình thang vuông là hình thang có một góc vuông
Dấu hiệu nhận biết: Hình thang có một góc vuông là hình thang vuông
3. Hình thang cân
a) Định nghĩa
Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.
Tứ giác ABCD là hình thang cân (đáy AB, CD)
\(\Leftrightarrow\left\{\begin{array}{l} A B / / \mathrm{CD} \\ {\left[\begin{array}{l} \widehat{C}=\widehat{D} \\ \widehat{A}=\widehat{B} \end{array}\right.} \end{array}\right.\)
Chú ý: Nếu ABCD là hình thang cân (đáy AB, CD) thì \(\hat{C}\) = \(\hat{D}\) và \(\hat{A} = \hat{B}\).
b) Tính chất
Định lí 1: Trong một hình thang cân, hai cạnh bên bằng nhau, ABCD là hình thang cân (đáy AB, CD) ⇒ AD = BC
Định lí 2: Trong một hình thang cân, hai đường chéo bằng nhau, ABCD là hình thang cân (đáy AB, CD) ⇒ AC = BD
Định lí 3: Hình thang có hai đường chéo bằng nhau là hình thang cân. Hình thang ABCD (đáy AB, CD) có AC = BD ⇒ ABCD là hình thang cân.
c) Dấu hiệu nhận biết
Hình thang có hai góc kề một đáy bằng nhau là hình thang cân.
Hình thang có hai đường chéo bằng nhau là hình thang cân.
4. Đường trung bình của tam giác
Định nghĩa: Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
Định lí:
Định lí 1: Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm của cạnh thứ ba,
Định lí 2: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
Δ ABC,AD = DB,AE = EC ⇒ DE//BC,DE = 1/2BC.
5. Đường trung bình của hình thang
Định nghĩa: Đường trung bình của hình thang là đoạn thẳng nối trung điểm hai cạnh bên của hình thang.
Định lý:
Định lí 1: Đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm cạnh bên thứ hai.
Định lí 2: Đường trung bình của hình thang thì song song với hai đáy và bằng nửa tổng hai đáy.
ABCD (AB//CD ),AE = ED,BF = FC ⇒ EF = (AB + CD)/2
6. Đối xứng trục
a) Hai điểm đối xứng với nhau qua đường thẳng
Hai điểm được gọi là đối xứng với nhau qua đường thẳng d nếu d là đường trung trực của đoạn thẳng nối hai điểm đó
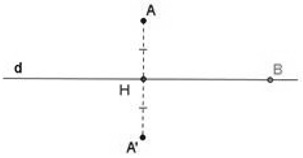
Quy ước: Nếu điểm B nằm trên đường thẳng d thì điểm đối xứng của B qua đường thẳng d cũng chính là điểm B.
b) Hai hình đối xứng qua một đường thẳng
Định nghĩa: Hai hình gọi là đối xứng với nhau qua đường thẳng d nếu mỗi điểm thuộc hình này đối xứng với một điểm thuộc hình kia qua đường thẳng d và ngược lại.
Đường thẳng d gọi là trục đối xứng của hai hình đó.
c) Hình có trục đối xứng
Đường thẳng d gọi là trục đối xứng của hình H nếu điểm đối xứng với mỗi điểm thuộc hình H qua đường thẳng d cũng thuộc hình H.
Ta nói rằng hình H có trục đối xứng.
Định lí: Đường thẳng đi qua trung điểm hai đáy của hình thang cân là trục đối xứng của hình thang đó.
7. Hình bình hành
a) Định nghĩa
Hình bình hành là tứ giác có các cạnh đối song song
Tứ giác ABCD là hình bình hành
\(\Leftrightarrow\left\{\begin{array}{l} A B / / C D \\ A D / / B C \end{array}\right.\)
b) Tính chất
Định lí: Trong hình bình hành:
+ Các cạnh đối bằng nhau.
+ Các góc đối bằng nhau.
+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường
c) Dấu hiệu nhận biết
+ Tứ giác có các cạnh đối song song là hình bình hành.
+ Tứ giác có các cạnh đối bằng nhau là hình bình hành.
+ Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
+ Tứ giác có các góc đối bằng nhau là hình bình hành.
+ Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
8. Đối xứng tâm
a) Hai điểm đối xứng qua một điểm
Định nghĩa: Hai điểm gọi là đối xứng với nhau qua điểm I nếu I là trung điểm của đoạn thẳng nối hai điểm đó.
b) Hai hình đối xứng qua một điểm
Định nghĩa: Hai hình gọi là đối xứng với nhau qua điểm I nếu mỗi điểm thuộc hình này đối xứng với một điểm thuộc hình kia qua điểm I và ngược lại.
c) Hình có tâm đối xứng
Định nghĩa: Điểm I gọi là tâm đối xứng qua hình H nếu điểm đối xứng với mỗi điểm thuộc hình H qua điểm I cũng thuộc hình H.
Định lí: Giao điểm hai đường chéo của hình bình hành là tâm đối xứng của hình bình hành đó.
9. Hình chữ nhật
a) Định nghĩa
Hình chữ nhật là tứ giác có bốn góc vuông. Hình chữ nhật cũng là một hình bình hành và cũng là hình thang cân
Tổng quát: ABCD là hình chữ nhật ⇔ Aˆ = Bˆ = Cˆ = Dˆ = 900
b) Tính chất
Hình chữ nhật là có tất cả các tính chất của hình bình hành và hình thang cân.
Định lí: Trong hình chữ nhật, hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường
c) Dấu hiệu nhận biết
+ Tứ giác có ba góc vuông là hình chữ nhật.
+ Hình thang cân có một góc vuông là hình chữ nhật.
+ Hình bình hành có một góc vuông là hình chữ nhật.
+ Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.
d) Áp dụng vào trong tam giác
+ Trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.
+ Nếu một tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh ấy thì tam giác đó là tam giác vuông.
10. Hình thoi
a) Định nghĩa
Hình thoi là tứ giác có bốn cạnh bằng nhau.
Hình thoi cũng là một hình bình hành.
Tổng quát: ABCD là hình thoi ⇔ AB = BC = CD = DA.
b) Tính chất
Hình thoi có tất cả các tính chất của hình bình hành.
Định lí: Trong hình thoi:
+ Hai đường chéo vuông góc với nhau.
+ Hai đường chéo là các đường phân giác các góc của hình thoi.
c) Dấu hiệu nhận biết
+ Tứ giác có bốn cạnh bằng nhau là hình thoi.
+ Hình bình hành có hai cạnh kề bằng nhau là hình thoi
+ Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.
+ Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi.
11. Hình vuông
a) Định nghĩa
Hình vuông là tứ giác có bốn góc vuông và có bốn cạnh bằng nhau.
Tổng quát: ABCD là hình vuông
\(\Leftrightarrow\left\{\begin{array}{l} \widehat{A}=\widehat{B}=\widehat{C}=\widehat{D}=90^{\circ} \\ A B=B C=C D=D A \end{array}\right.\)
Nhận xét:
+ Hình vuông là hình chữ nhật có bốn cạnh bằng nhau.
+ Hình vuông là hình thoi có bốn góc vuông.
+ Hình vuông vừa là hình chữ nhật vừa là hình thoi.
b) Tính chất
Hình vuông có tất cả các tính chất của hình chữ nhật và hình thoi.
c) Dấu hiệu nhận biết
+ Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.
+ Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.
+ Hình chữ nhật có một đường chéo là đường phân giác một góc là hình vuông.
+ Hình thoi có một góc vuông là hình vuông.
+ Hình thoi có hai đường chéo bằng nhau là hình vuông.
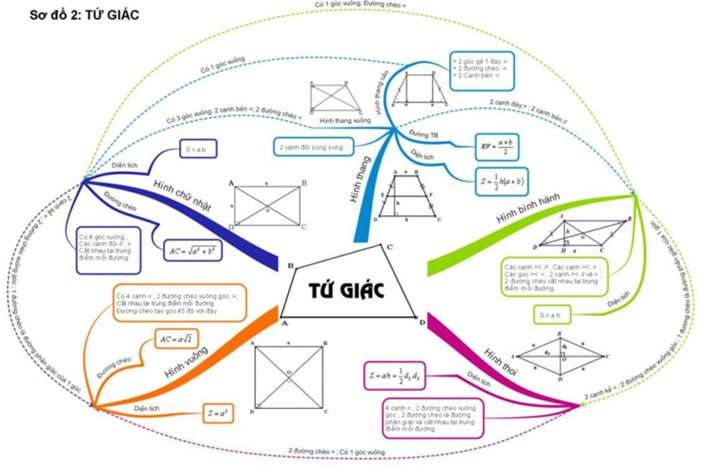
Sơ đồ tư duy chương I: Tứ giác
Mẫu 1
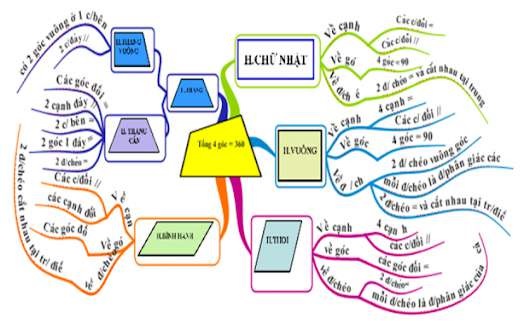
Mẫu 2
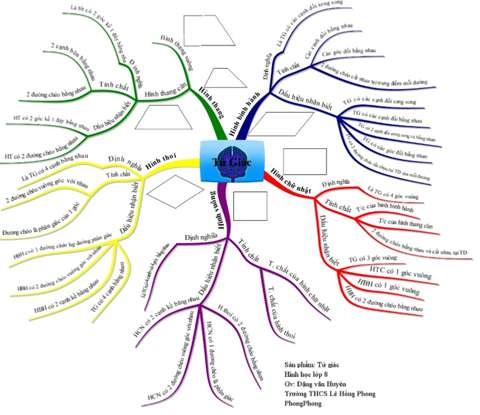
Mẫu 3
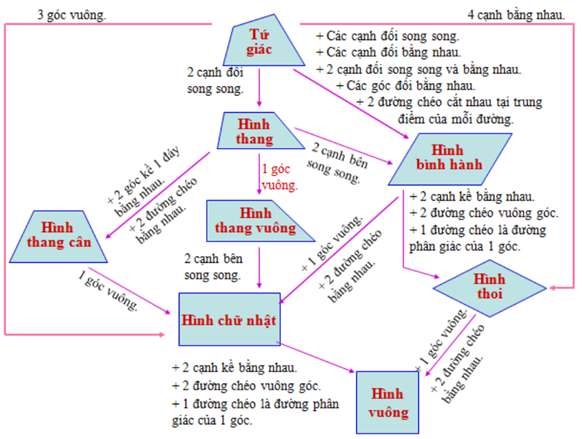
Mẫu 4
Ngoài ra, VnDoc.com đã thành lập group chia sẻ tài liệu học tập THCS miễn phí trên Facebook: Tài liệu học tập lớp 8. Mời các bạn học sinh tham gia nhóm, để có thể nhận được những tài liệu mới nhất.
Sơ đồ tư duy Hình học 8 chương 1 được VnDoc chia sẻ trên đây. Hy vọng với tài liệu này sẽ giúp ích cho các em học sinh nắm chắc kiến thứ, từ đó vận dụng tốt giải các bài tập Toán THCS. Chúc các em học tốt, nếu thấy tài liệu hữu ích hãy chia sẻ cho các bạn cùng tham khảo nhé
Ngoài Sơ đồ tư duy Hình học 8 chương 1. Các em có thể tham khảo thêm các bài tập Toán 8 hoặc liên quan môn Toán như Giải Toán 8, Giải Vở BT Toán 8, Giải SBT Toán 8, hoặc để chuẩn bị tốt cho kì thi sắp tới các em truy cập đề thi giữa học kì 1 lớp 8 được VnDoc cập nhật đề thi từ các trường THCS trên cả nước
