Bộ câu hỏi ôn thi đánh giá tư duy phần Toán học - Số 12
ĐGNL năm 2025
Dạng tài liệu:
Đề thi Toán ĐGNL-ĐGTD
Phân loại:
Tài liệu Tính phí
Trang 1 | 86
Bộ câu hỏi ôn thi đánh giá tư duy phần Toán học
Câu 1:
Cho hàm số .
Mỗi phát biểu sau đây là đúng hay sai?
Phát biểu
ĐÚNG
SAI
Với hàm số liên tục trái tại .
Với hàm số liên tục phải tại .
Với hàm số liên tục tại .
Lời giải:
Ta có:
a) Để liên tục trái tại tồn tại và .
Ta có: và .
Vậy với hàm số liên tục trái tại .
b) Để liên tục phải tại tồn tại và .
Ta có: và .
Vậy với hàm số liên tục phải tại .
Trang 2 | 86
c) Do nên hàm số không liên tục tại .
Do đó ta chọn đáp án như sau
Phát biểu
ĐÚNG
SAI
Với hàm số liên tục trái tại .
¤
¡
Với hàm số liên tục phải tại .
¡
¤
Với hàm số liên tục tại .
¡
¤
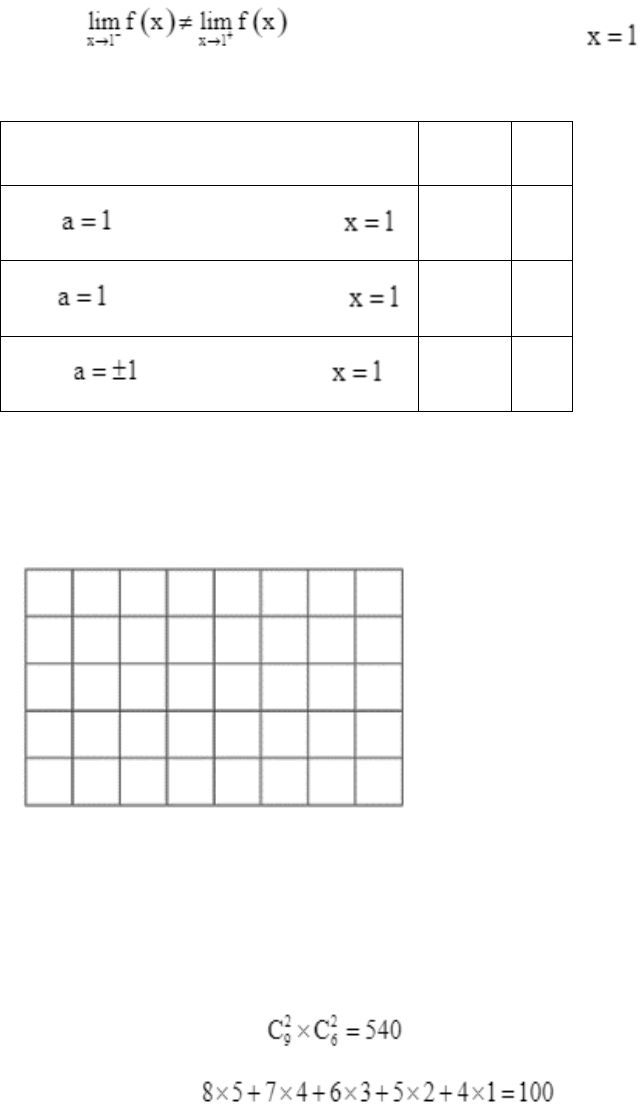
Câu 2:
Điền các số nguyên dương thích hợp vào những chỗ trống.
Cho bảng ô vuông sau:
Số hình chữ nhật có trên hình là: (1) _________.
Số hình vuông có trên hình là: (2) _________.
Lời giải:
Cứ hai đường kẻ ngang phân biệt và 2 đường kẻ dọc phân biệt cho ta một hình chữ nhật.
Vậy số hình chữ nhật là: .
Số hình vuông là: .
Do đó ta điền đáp án như sau
Số hình chữ nhật có trên hình là: (1) 540.
Số hình vuông có trên hình là: (2) 100.
Trang 3 | 86
Câu 3:
Cho hàm số . Biết là giá trị để hàm số liên tục tại ,
khi đó số nghiệm nguyên của bất phương trình là (1) _____.
Lời giải:
Ta có:
Đặt .
Hàm số liên tục tại .
Để tồn tại thì .
Với thì .
Bất phương trình trở thành: .
Vì nguyên nên . Vậy bất phương trình có 5 nghiệm nguyên.
Do đó ta điền đáp án như sau
Cho hàm số . Biết là giá trị để hàm số liên tục tại ,
khi đó số nghiệm nguyên của bất phương trình là (1) 5.
Câu 4:
Đề ôn thi đánh giá tư duy phần Toán học
VnDoc.com xin gửi tới bạn đọc bài viết Bộ câu hỏi ôn thi đánh giá tư duy trường Đại học Bách Khoa phần Toán học - Số 12 có đáp án kèm theo để bạn đọc cùng tham khảo nhé. Bài viết được tổng hợp gồm có 40 câu hỏi phần Toán. Đề có đáp án và lời giải chi tiết kèm theo. Mời các bạn cùng theo dõi bài viết dưới đây để có thêm tài liệu ôn thi đánh giá năng lực sắp tới nhé.
