Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

Đóng

Điểm danh hàng ngày

Hôm nay +3
Ngày 2 +3
Ngày 3 +3
Ngày 4 +3
Ngày 5 +3
Ngày 6 +3
Ngày 7 +5

Bạn đã điểm danh Hôm nay và nhận 3 điểm! Đăng nhập ngay để nhận điểm

Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169

VnDoc.com

Cách xác định góc giữa hai mặt bên

Bài tập Toán 11 Góc trong không gian có đáp án

Bài trước

Tải về

Bài sau

Lớp: Lớp 11

Môn: Toán

Dạng tài liệu: Chuyên đề

Loại: Tài liệu Lẻ

Mức độ: Trung bình

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Phương pháp tính góc giữa hai mặt bên trong không gian

A. Hướng dẫn xác định góc giữa hai mặt bên
B. Bài tập minh họa xác định góc giữa hai mặt bên
C. Bài tập tự rèn luyện có hướng dẫn giải chi tiết

Trong các bài toán góc trong không gian Toán 11, dạng xác định góc giữa hai mặt bên thường khiến học sinh lúng túng do phải lựa chọn đúng giao tuyến và mặt phẳng phụ hợp lý. Nếu không hiểu rõ bản chất hình học, việc xác định góc rất dễ sai hướng.

Bài viết này sẽ hướng dẫn cách xác định góc giữa hai mặt bên theo phương pháp rõ ràng, kèm bài tập có đáp án, giúp người học tiếp cận bài toán chính xác và hiệu quả.

A. Hướng dẫn xác định góc giữa hai mặt bên

Hình vẽ minh họa:

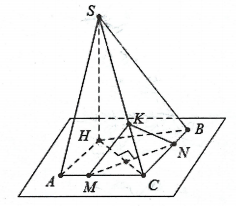
Tính góc giữa hai mặt bên $(SAC)$ và $(SBC).$

Cách 1: Tính góc giữa 2 đường thẳng $a$ và $b$ lần lượt vuông góc với mặt phẳng $(SAC)$ và $(SBC).$

Cách 2: Dựng đường cao $SH\bot(ABC).$ $SH\bot(ABC).$

Lấy điểm $M$ bất kỳ thuộc $AC,$ dựng $MN\bot HC.$ $MN\bot HC.$
Lại có: $MN\bot SH \Rightarrow MN\bot(SHC) \Rightarrow MN\bot SC.$ $MN\bot SH \Rightarrow MN\bot(SHC) \Rightarrow MN\bot SC.$
Dựng $MK\bot SC \Rightarrow SC\bot(MKN)$ $MK\bot SC \Rightarrow SC\bot(MKN)$ $\Rightarrow \left( \widehat{(SAC);(SBC)} \right) = \widehat{(MK,KN).}$ $\Rightarrow \left( \widehat{(SAC);(SBC)} \right) = \widehat{(MK,KN).}$

B. Bài tập minh họa xác định góc giữa hai mặt bên

Ví dụ 1: Cho hình chóp $S.ABC$ có $SA$ vuông góc với mặt phẳng $(ABC),$ đáy $ABC$ tam giác vuông tại $B$ có $AB = a,\ \ BC = a\sqrt{3}.$ $AB = a,\ \ BC = a\sqrt{3}.$ Biết $SA = \frac{a\sqrt{6}}{2},$ $SA = \frac{a\sqrt{6}}{2},$ tính góc giữa hai mặt phẳng $(SAC)$ và $(SBC).$

Hướng dẫn giải

Hình vẽ minh họa:

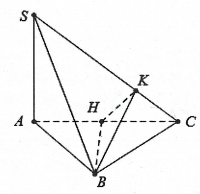
Dựng $BH\bot AC \Rightarrow BH\bot(SAC) \Rightarrow BH\bot SC.$ $BH\bot AC \Rightarrow BH\bot(SAC) \Rightarrow BH\bot SC.$

Dựng $HK\bot SC \Rightarrow (HKB)\bot SC \Rightarrow \widehat{\left( (SBC);(SAC) \right)} = \widehat{HKB}.$ $HK\bot SC \Rightarrow (HKB)\bot SC \Rightarrow \widehat{\left( (SBC);(SAC) \right)} = \widehat{HKB}.$

Ta có: $SA = \sqrt{SB^{2} - AB^{2}} = \frac{a\sqrt{2}}{2};\ \ AC = \sqrt{AB^{2} + BC^{2}} = 2a.$ $SA = \sqrt{SB^{2} - AB^{2}} = \frac{a\sqrt{2}}{2};\ \ AC = \sqrt{AB^{2} + BC^{2}} = 2a.$

Khi đó $\sin\widehat{KCH} = \frac{HK}{HC} = \frac{SA}{SC} = \frac{SA}{\sqrt{SA^{2} + AC^{2}}} = \frac{1}{3} \Rightarrow HK = \frac{a}{3}.$ $\sin\widehat{KCH} = \frac{HK}{HC} = \frac{SA}{SC} = \frac{SA}{\sqrt{SA^{2} + AC^{2}}} = \frac{1}{3} \Rightarrow HK = \frac{a}{3}.$

Mặt khác: $BH = \frac{BA.BC}{AC} = \frac{a\sqrt{3}}{2} \Rightarrow \tan\widehat{HKB} = \frac{BH}{HK} = \sqrt{3}$ $BH = \frac{BA.BC}{AC} = \frac{a\sqrt{3}}{2} \Rightarrow \tan\widehat{HKB} = \frac{BH}{HK} = \sqrt{3}$

$\Rightarrow \widehat{HKB} = 60^{o}.$ $\Rightarrow \widehat{HKB} = 60^{o}.$ Vậy góc giữa hai mặt phẳng $(SAC)$ và $(SBC)$ bằng 60^o.

Ví dụ 2: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thoi cạnh $a$ có $\widehat{ABC} = 60^{o},$ $\widehat{ABC} = 60^{o},$ $SA\bot(ABC)$ $SA\bot(ABC)$ và $SA = a.$ Tính cosin góc giữa:

a) $(SBC)$à $(SCD).$ b) $(SAD)$ và $(SCD).$

Hướng dẫn giải

Hình vẽ minh họa:

a) Nhận xét $\Delta ABC$ $\Delta ABC$ là tam giác đều cạnh $a$ vì $AB = BC = a$ và $\widehat{ABC} = 60^{o}.$ $\widehat{ABC} = 60^{o}.$ Gọi $O$ là tâm của hình thoi $ABCD.$

Ta có: $\left\{ \begin{matrix} BD\bot AC \\ BD\bot SA \end{matrix} \right.\ \Rightarrow BD\bot(SAC) \Rightarrow BD\bot SC.$ $\left\{ \begin{matrix} BD\bot AC \\ BD\bot SA \end{matrix} \right.\ \Rightarrow BD\bot(SAC) \Rightarrow BD\bot SC.$

Dựng $BE\bot SC \Rightarrow SC\bot(BED).$ $BE\bot SC \Rightarrow SC\bot(BED).$

Mặt khác: $SA = AC = a \Rightarrow \Delta SAC$ $SA = AC = a \Rightarrow \Delta SAC$ vuông cân tại $A$ suy ra

$\widehat{ECO} = 45^{o}.$ $\widehat{ECO} = 45^{o}.$ Khi đó $OE = OCsin45^{o} = \frac{a\sqrt{2}}{4}.$ $OE = OCsin45^{o} = \frac{a\sqrt{2}}{4}.$

Lại có: $OB = \frac{a\sqrt{3}}{2} \Rightarrow \tan\widehat{BEO} = \frac{OB}{OE} = \sqrt{6}.$ $OB = \frac{a\sqrt{3}}{2} \Rightarrow \tan\widehat{BEO} = \frac{OB}{OE} = \sqrt{6}.$

Do $\widehat{BED} = 2\widehat{BEO}$ $\widehat{BED} = 2\widehat{BEO}$ sử dụng công thức lượng giác hoặc máy tính CASIO ta tính được $\cos\widehat{BED} = \frac{- 5}{7}$ $\cos\widehat{BED} = \frac{- 5}{7}$

Cách khác:

Ta có: $BE = DE = \sqrt{OE^{2} + OB^{2}} = \frac{\sqrt{14}}{4}$ $BE = DE = \sqrt{OE^{2} + OB^{2}} = \frac{\sqrt{14}}{4}$

$\Rightarrow \cos\widehat{BED} = \frac{EB^{2} + ED^{2} - BD^{2}}{2.EB.ED} = \frac{- 5}{7}.$ $\Rightarrow \cos\widehat{BED} = \frac{EB^{2} + ED^{2} - BD^{2}}{2.EB.ED} = \frac{- 5}{7}.$

Suy ra $\cos\widehat{\left( (SBC);(SCD) \right)} = \frac{5}{7}.$ $\cos\widehat{\left( (SBC);(SCD) \right)} = \frac{5}{7}.$

b) Dựng $CM\bot AD$ $CM\bot AD$ ta có: $\left\{ \begin{matrix} CM\bot AD \\ CM\bot SA \end{matrix} \right.\ \Rightarrow CM\bot(SAD) \Rightarrow CM\bot SD.$ $\left\{ \begin{matrix} CM\bot AD \\ CM\bot SA \end{matrix} \right.\ \Rightarrow CM\bot(SAD) \Rightarrow CM\bot SD.$

Dựng $CK\bot SD \Rightarrow SD\bot(MKC).$ $CK\bot SD \Rightarrow SD\bot(MKC).$

Tam giác $ACD$ đều cạnh $a$ nên $CM = \frac{a\sqrt{3}}{2}.$ $CM = \frac{a\sqrt{3}}{2}.$

Do $SA = AD = a \Rightarrow \Delta SAD$ $SA = AD = a \Rightarrow \Delta SAD$ vuông cân tại $A$ suy ra $\widehat{SDM} = 45^{o}.$ $\widehat{SDM} = 45^{o}.$

Do đó $MK = MDsin45^{o} = \frac{a\sqrt{2}}{4}.$ $MK = MDsin45^{o} = \frac{a\sqrt{2}}{4}.$

Suy ra $\tan\widehat{MKC} = \frac{CM}{MK} = \sqrt{6} \Rightarrow \cos\widehat{MKC} = \frac{1}{\sqrt{7}}.$ $\tan\widehat{MKC} = \frac{CM}{MK} = \sqrt{6} \Rightarrow \cos\widehat{MKC} = \frac{1}{\sqrt{7}}.$

Vậy $\cos\widehat{\left( (SCD);(SAD) \right)} = \frac{1}{\sqrt{7}}.$ $\cos\widehat{\left( (SCD);(SAD) \right)} = \frac{1}{\sqrt{7}}.$

C. Bài tập tự rèn luyện có hướng dẫn giải chi tiết

Bài tập 1. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là nửa lục giác đều cạnh $a$ với $AD = 2a,$ biết rằng $SA\bot(ABCD)$ $SA\bot(ABCD)$ và mặt phẳng $(SCD)$ tạo với đáy một góc 45^o. Tính cosin góc giữa 2 mặt phẳng $(SCD)$ và $(SBC).$

Bài tập 2. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật với $AB = a;\ \ AD = a\sqrt{3},$ $AB = a;\ \ AD = a\sqrt{3},$ cạnh bên $SA\bot(ABCD).$ $SA\bot(ABCD).$ Biết mặt phẳng $(SBC)$ tạo với mặt đáy một góc 60^o. Tính cosin góc giữa hai mặt phẳng $(SBC)$ và $(SCD).$

Bài tập 3. Cho hình chóp $S.ABCD$ có đáy là hình vuông tâm $O,$ cạnh $a.$ Biết $SA\bot(ABCD),$ $SA\bot(ABCD),$ tính độ dài đoạn thẳng $SA$ để góc giữa mặt phẳng $(SBC)$ và $(SCD)$ bằng 60^o.

📄 Do dung lượng nội dung lớn, tài liệu chi tiết được cung cấp dưới dạng file tải về.

-----------------------------------------------

Khi nắm vững phương pháp xác định góc giữa hai mặt bên, học sinh sẽ giải quyết các bài toán góc trong không gian một cách tự tin và chính xác hơn. Hệ thống bài tập Toán 11 có đáp án giúp củng cố kỹ năng, hạn chế sai sót và nâng cao khả năng vận dụng trong các dạng bài tương tự.

Xem thử Tải về

Chọn file muốn tải về: