Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

Đóng

Điểm danh hàng ngày

Hôm nay +3
Ngày 2 +3
Ngày 3 +3
Ngày 4 +3
Ngày 5 +3
Ngày 6 +3
Ngày 7 +5

Bạn đã điểm danh Hôm nay và nhận 3 điểm! Đăng nhập ngay để nhận điểm

Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169

VnDoc.com

Xác định góc giữa cạnh bên và mặt phẳng đáy

Tính góc trong không gian Toán 11 có đáp án

Bài trước

Tải về

Bài sau

Lớp: Lớp 11

Môn: Toán

Dạng tài liệu: Chuyên đề

Mức độ: Trung bình

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Cách tính góc giữa cạnh bên và mặt phẳng đáy Toán 11

A. Cách xác định góc giữa cạnh bên và mặt đáy
B. Bài tập ví dụ minh họa tìm góc giữa cạnh bên và mặt đáy

Trong chương Tính góc trong không gian Toán 11, dạng toán xác định góc giữa cạnh bên và mặt phẳng đáy thường khiến học sinh gặp khó khăn do phải lựa chọn đúng đường vuông góc và hình chiếu phù hợp. Nếu không hiểu rõ bản chất, việc xác định góc rất dễ sai.
Bài viết này sẽ hướng dẫn cách xác định góc giữa cạnh bên và mặt phẳng đáy theo phương pháp rõ ràng, giúp người học tiếp cận bài toán chính xác và hiệu quả.

A. Cách xác định góc giữa cạnh bên và mặt đáy

Hình vẽ minh họa:

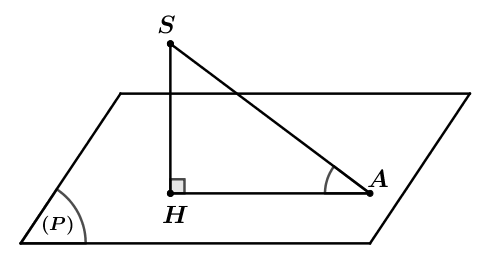
Tìm góc giữa cạnh bên SA và mặt đáy (ABC)

Gọi H là hình chiếu vuông góc của S trên mặt phẳng đáy (ABC).

Như vậy HA là hình chiếu vuông góc của SA trên (ABC).

Vậy $\widehat{\left( SA;(ABC) \right)} = \widehat{(SA;HA)} = \widehat{SAH}$ $\widehat{\left( SA;(ABC) \right)} = \widehat{(SA;HA)} = \widehat{SAH}$.

B. Bài tập ví dụ minh họa tìm góc giữa cạnh bên và mặt đáy

Ví dụ 1: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, có $AB = a;BC = a\sqrt{3}$ $AB = a;BC = a\sqrt{3}$. Biết SA⊥(ABC), SB tạo với đáy một góc 60⁰ và M là trung điểm của BC

a) Tính cosin góc giữa SC và mặt phẳng (ABC).

b) Tính cosin góc giữa SM và mặt phẳng (ABC).

Hướng dẫn giải

Hình vẽ minh họa:

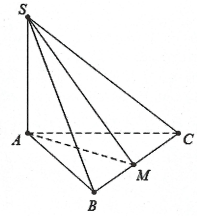
a) Do $SA\bot(ABC) \Rightarrow \widehat{\left( SB;(ABC) \right)} = \widehat{SBA} = 60{^\circ}$ $SA\bot(ABC) \Rightarrow \widehat{\left( SB;(ABC) \right)} = \widehat{SBA} = 60{^\circ}$.

Do đó $SA = AB\tan\widehat{SBA} = atan60{^\circ} = a\sqrt{3}$ $SA = AB\tan\widehat{SBA} = atan60{^\circ} = a\sqrt{3}$.

Ta có: $AC = \sqrt{AB^{2} + BC^{2}} = 2a;\widehat{\left( SC;(ABC) \right)} = \widehat{SCA}$ $AC = \sqrt{AB^{2} + BC^{2}} = 2a;\widehat{\left( SC;(ABC) \right)} = \widehat{SCA}$.

Khi đó: $\cos\widehat{SCA} = \frac{AC}{SC} = \frac{AC}{\sqrt{SA^{2} + AC^{2}}} = \frac{2a}{\sqrt{3a^{2} + 4a^{2}}} = \frac{2}{\sqrt{7}}$ $\cos\widehat{SCA} = \frac{AC}{SC} = \frac{AC}{\sqrt{SA^{2} + AC^{2}}} = \frac{2a}{\sqrt{3a^{2} + 4a^{2}}} = \frac{2}{\sqrt{7}}$.

b) Do $SA\bot(ABC) \Rightarrow \widehat{\left( SM;(ABC) \right)} = \widehat{SMA} = \varphi$ $SA\bot(ABC) \Rightarrow \widehat{\left( SM;(ABC) \right)} = \widehat{SMA} = \varphi$.

Ta có: $AM = \sqrt{AB^{2} + BM^{2}} = \sqrt{a^{2} + \left( \frac{a\sqrt{3}}{2} \right)^{2}} = \frac{a\sqrt{7}}{2}$ $AM = \sqrt{AB^{2} + BM^{2}} = \sqrt{a^{2} + \left( \frac{a\sqrt{3}}{2} \right)^{2}} = \frac{a\sqrt{7}}{2}$.

Khi đó $\cos\varphi = \frac{AM}{SM} = \frac{AM}{\sqrt{SA^{2} + AM^{2}}} = \frac{\sqrt{133}}{19}$ $\cos\varphi = \frac{AM}{SM} = \frac{AM}{\sqrt{SA^{2} + AM^{2}}} = \frac{\sqrt{133}}{19}$.

Ví dụ 2: Cho hình chóp S.ABCD, đáy là hình chữ nhật có AB = 2a; AD = a. Tam giác SAB đều và thuộc mặt phẳng vuông góc với đáy.

a) Tính góc giữa SB; SC và mặt phẳng (ABCD).

b) Gọi I là trung điểm của BC. Tính tan góc giữa SI và mặt phẳng (ABCD).

Hướng dẫn giải

Hình vẽ minh họa:

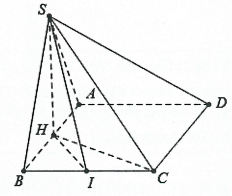
a) Gọi H là trung điểm của AB ta có: $SH\bot AB$ $SH\bot AB$.

Mặt khác $\left\{ \begin{matrix} (SAB)\bot(ABCD) \\ AB = (SAB) \cap (ABCD) \end{matrix} \right.\ \Rightarrow SH\bot(ABCD)$ $\left\{ \begin{matrix} (SAB)\bot(ABCD) \\ AB = (SAB) \cap (ABCD) \end{matrix} \right.\ \Rightarrow SH\bot(ABCD)$.

Tam giác SAB đều cạnh 2a nên $SH = a\sqrt{3}$ $SH = a\sqrt{3}$.

$HC = \sqrt{HB^{2} + BC^{2}} = a\sqrt{2}$ $HC = \sqrt{HB^{2} + BC^{2}} = a\sqrt{2}$.

Do $SH\bot(ABCD) \Rightarrow \widehat{\left( SB;(ABCD) \right)} = \widehat{SBH} = 60{^\circ}$ $SH\bot(ABCD) \Rightarrow \widehat{\left( SB;(ABCD) \right)} = \widehat{SBH} = 60{^\circ}$

$\widehat{\left( SC;(ABCD) \right)} = \widehat{SCH}$ $\widehat{\left( SC;(ABCD) \right)} = \widehat{SCH}$ và $\tan\widehat{SCH} = \frac{SH}{HC} = \sqrt{\frac{3}{2}}$ $\tan\widehat{SCH} = \frac{SH}{HC} = \sqrt{\frac{3}{2}}$.

b) Ta có: $HI = \sqrt{HB^{2} + BI^{2}} = \sqrt{a^{2} + \left( \frac{a}{2} \right)^{2}} = \frac{a\sqrt{5}}{2}$ $HI = \sqrt{HB^{2} + BI^{2}} = \sqrt{a^{2} + \left( \frac{a}{2} \right)^{2}} = \frac{a\sqrt{5}}{2}$.

Mặt khác $\widehat{\left( SI;(ABCD) \right)} = \widehat{SIH}$ $\widehat{\left( SI;(ABCD) \right)} = \widehat{SIH}$ và $\tan\widehat{SIH} = \frac{SH}{SI} = a\sqrt{3}:\frac{a\sqrt{5}}{2} = \frac{2\sqrt{15}}{5}$ $\tan\widehat{SIH} = \frac{SH}{SI} = a\sqrt{3}:\frac{a\sqrt{5}}{2} = \frac{2\sqrt{15}}{5}$.

Ví dụ 3: Cho hình chóp S.ABCD; có đáy là nửa lục giác đều cạnh a, AD = 2a. Biết SA⊥(ABCD) và đường thẳng SB tạo với đáy một góc 45⁰.

a) Tính cosin góc tạo bởi các cạnh SC; SD và mặt đáy (ABCD).

b) Gọi I là trung điểm của CD tính tan góc tạo bởi SI và mặt phẳng (ABCD).

Hướng dẫn giải

Hình vẽ minh họa:

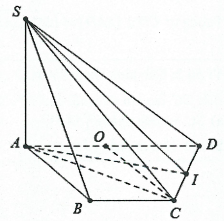
a) Gọi O là trung điểm của AD => OABC là hình thoi cạnh a

$\Rightarrow CO = a = \frac{1}{2}AD \Rightarrow \Delta ACD$ $\Rightarrow CO = a = \frac{1}{2}AD \Rightarrow \Delta ACD$ vuông tại C.

Do $SA\bot(ABCD) \Rightarrow \widehat{\left( SB;(ABCD) \right)} = \widehat{SBA} = 45{^\circ}$ $SA\bot(ABCD) \Rightarrow \widehat{\left( SB;(ABCD) \right)} = \widehat{SBA} = 45{^\circ}$.

Do đó SA = AB.tan45⁰ = a

$AC = \sqrt{AD^{2} - CD^{2}} = a\sqrt{3}$ $AC = \sqrt{AD^{2} - CD^{2}} = a\sqrt{3}$

$\Rightarrow \cos\widehat{\left( SC;(ABC) \right)} = \cos\widehat{SCA}$ $\Rightarrow \cos\widehat{\left( SC;(ABC) \right)} = \cos\widehat{SCA}$

$= \frac{AC}{SC} = \frac{AC}{\sqrt{SA^{2} + AC^{2}}} = \frac{a\sqrt{3}}{\sqrt{a^{2} + 3a^{2}}} = \frac{\sqrt{3}}{2}$ $= \frac{AC}{SC} = \frac{AC}{\sqrt{SA^{2} + AC^{2}}} = \frac{a\sqrt{3}}{\sqrt{a^{2} + 3a^{2}}} = \frac{\sqrt{3}}{2}$.

$\cos\widehat{\left( SD;(ABCD) \right)} = \cos\widehat{SDA} = \frac{AD}{\sqrt{SA^{2} + AD^{2}}} = \frac{2}{\sqrt{5}}$ $\cos\widehat{\left( SD;(ABCD) \right)} = \cos\widehat{SDA} = \frac{AD}{\sqrt{SA^{2} + AD^{2}}} = \frac{2}{\sqrt{5}}$.

b) Ta có: $AI = \sqrt{AC^{2} + CI^{2}} = \sqrt{3a^{2} + \left( \frac{a}{2} \right)^{2}} = \frac{a\sqrt{13}}{2}$ $AI = \sqrt{AC^{2} + CI^{2}} = \sqrt{3a^{2} + \left( \frac{a}{2} \right)^{2}} = \frac{a\sqrt{13}}{2}$.

Do đó $\tan\widehat{\left( SI;(ABCD) \right)} = \tan\widehat{SIA} = \frac{SA}{AI} = \frac{2}{\sqrt{13}}$ $\tan\widehat{\left( SI;(ABCD) \right)} = \tan\widehat{SIA} = \frac{SA}{AI} = \frac{2}{\sqrt{13}}$.

--------------------

FAQ – Xác Định Góc Giữa Cạnh Bên Và Mặt Phẳng Đáy

1. Góc giữa cạnh bên và mặt phẳng đáy là gì?

Góc giữa cạnh bên và mặt phẳng đáy là góc tạo bởi cạnh bên với hình chiếu vuông góc của cạnh bên đó lên mặt phẳng đáy.

Đây là một trong những khái niệm quan trọng của chuyên đề góc trong không gian Toán 11.

2. Làm thế nào để xác định góc giữa cạnh bên và mặt phẳng đáy?

Để xác định góc giữa cạnh bên và mặt phẳng đáy, học sinh thường thực hiện các bước:

Xác định hình chiếu vuông góc của đỉnh lên mặt phẳng đáy.
Xác định hình chiếu của cạnh bên trên mặt phẳng đáy.
Tìm góc giữa cạnh bên và hình chiếu của nó.

Phương pháp này được áp dụng trong hầu hết các bài toán hình học không gian lớp 11.

3. Tại sao phải tìm hình chiếu vuông góc trước khi tính góc?

Hình chiếu vuông góc giúp chuyển bài toán không gian về bài toán phẳng dễ xử lý hơn.

Thông qua tam giác vuông tạo thành bởi cạnh bên, đường cao và hình chiếu, học sinh có thể áp dụng các hệ thức lượng để tính góc chính xác.

4. Góc giữa cạnh bên và mặt phẳng đáy thường xuất hiện trong những hình nào?

Dạng toán này thường gặp trong:

Hình chóp đều.
Hình chóp tứ giác đều.
Hình chóp tam giác đều.
Hình chóp có cạnh bên vuông góc với đáy.
Các bài toán hình học không gian tổng hợp.

Đây là những mô hình quen thuộc trong chương trình Toán 11.

5. Công cụ nào thường được sử dụng để tính góc trong không gian?

Khi giải bài toán tính góc, học sinh thường sử dụng:

Định lý Pythagore.
Các tỉ số lượng giác trong tam giác vuông.
Hệ thức về đường cao.
Quan hệ vuông góc trong không gian.

Việc kết hợp linh hoạt các kiến thức này giúp lời giải ngắn gọn và chính xác.

6. Những sai lầm thường gặp khi xác định góc giữa cạnh bên và mặt phẳng đáy là gì?

Một số lỗi phổ biến gồm:

Chọn sai hình chiếu của cạnh bên.
Nhầm lẫn giữa góc trong mặt đáy và góc cần tìm.
Vẽ hình không chính xác.
Xác định sai quan hệ vuông góc.

--------------------------

Khi nắm vững phương pháp xác định góc giữa cạnh bên và mặt phẳng đáy, học sinh sẽ giải quyết các bài toán tính góc trong không gian một cách tự tin hơn. Việc hiểu rõ bản chất hình học giúp tránh nhầm lẫn, đồng thời nâng cao khả năng vận dụng trong các dạng bài Toán 11 liên quan.

Xem thử Tải về

Chọn file muốn tải về: