Cách tính góc giữa đường cao và mặt bên
Góc trong không gian Toán 11 - Có đáp án
Trong các bài toán Toán 11, dạng tính góc giữa đường cao và mặt bên đòi hỏi học sinh phải xác định đúng hình chiếu và mối quan hệ vuông góc liên quan. Nếu không nắm vững cách dựng và chọn góc, lời giải rất dễ sai bản chất. Bài viết này sẽ hướng dẫn cách tính góc giữa đường cao và mặt bên theo phương pháp rõ ràng, kèm bài tập minh họa, giúp người học hiểu đúng và vận dụng hiệu quả khi làm bài.
A. Cách xác định góc giữa đường cao và mặt bên
Hình vẽ minh họa:
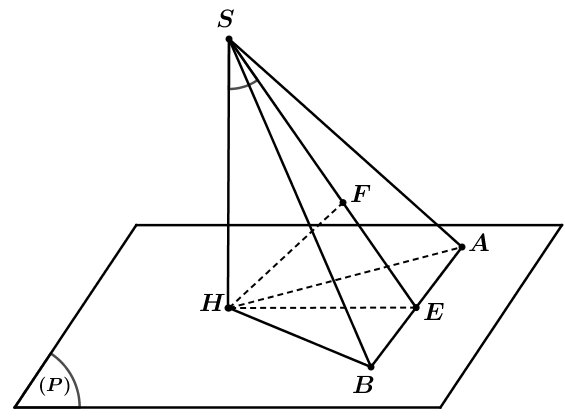
- Tìm góc giữa đường cao SH và mặt phẳng
\((SAB)\). - Dựng \(HE\bot AB,HF\bot SE\).
- Ta có: \(AB\bot SH \Rightarrow AB\bot(SHE)
\Rightarrow AB\bot HF\).
- Mặt khác \(HF\bot SE \Rightarrow
HF\bot(SAB) \Rightarrow F\) là hình chiếu vuông góc của H trên mặt phẳng \((SAB)\)
- Vậy \(\widehat{\left( SH;(SAB) \right)} =
\widehat{(HF;SF)} = \widehat{HSF}\).
B. Bài tập minh họa tính góc giữa đường thẳng và mặt bên
Ví dụ 1: Cho hình chóp \(S.ABC,\)có đáy \(ABC\) là tam giác đều cạnh \(2a.\)Cạnh bên \(SA = a\sqrt{3}\) và vuông góc với đáy. Tính góc giữa \(SA\) và mặt phẳng \((SBC)\).
Hướng dẫn giải
Hình vẽ minh họa:
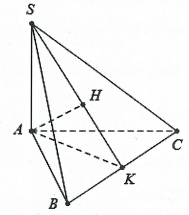
Từ \(A\) kẻ \(AK\) vuông góc với \(BC\) tại \(K\). Ta có: \(SA\bot BC\) và \(AK\bot BC\)
\(\Rightarrow BC\bot(SAK)\).
Kẻ \(AH\bot SK,H \in SK\). Mà \(BC\bot AH\) suy ra \(AH\bot(SBC)\)
\(\Rightarrow \widehat{\left( SA;(SBC)
\right)} = \widehat{ASH} = \widehat{ASK}\).
Tam giác \(SAK\) vuông tại \(A\), có \(SA = AK
= a\sqrt{3} \Rightarrow\) tam giác \(SAK\) vuông cân tại \(A\) nên \(\widehat{ASK} = 45{^\circ}\).
Vậy \(\widehat{\left( SA;(SBC) \right)} =
45{^\circ}\).
Ví dụ 2: Cho hình chóp \(S.ABCD\) có đáy là hình chữ nhật có \(AB = a,AD = 2a,SA =
2a\) và \(SA\bot(ABCD)\). Tính tan góc giữa \(SA\) và các mặt phẳng \((SBC),(SBD)\) và \((SCD)\).
Hướng dẫn giải
Hình vẽ minh họa:
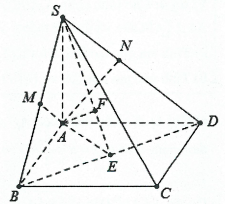
Do \(\left\{ \begin{matrix}
BC\bot AB \\
BC\bot SA
\end{matrix} \right.\ \Rightarrow BC\bot(SAB)\).
Dựng \(AM\bot SB \Rightarrow AM\bot(SBC)
\Rightarrow M\) là hình chiếu vuông góc của \(A\) trên \((SBC)\).
Khi đó: \(\widehat{\left( SA;(SBC) \right)}
= \widehat{ASM} = \widehat{ASB} = \alpha\).
Do đó \(\tan\alpha = \frac{AB}{SA} =
\frac{1}{2}\).
Tương tự ta có: \(\widehat{\left( SA;(SCD)
\right)} = \widehat{ASD} = \beta\) và \(\tan\beta = \frac{AD}{SA} = 1\).
Dựng \(AE\bot BD,AF\bot SE\) ta có: \(\left\{ \begin{matrix}
BD\bot AE \\
BD\bot SA
\end{matrix} \right.\)
\(\Rightarrow BD\bot(SAE) \Rightarrow
BD\bot AF\).
Mặt khác \(AF\bot SE \Rightarrow
AF\bot(SBD)\)
\(\Rightarrow \widehat{\left( SA;(SBD)
\right)} = \widehat{ASF} = \widehat{ASE}\).
Khi đó \(\tan\widehat{ASE} =
\frac{AE}{SA}\), trong đó \(AE =
\frac{AB.AD}{\sqrt{AB^{2} + AD^{2}}} = \frac{2a}{\sqrt{5}}\)
\(\Rightarrow \tan\widehat{ASE} =
\frac{AE}{SA} = \frac{1}{\sqrt{5}}\).
C. Bài tập tự rèn luyện có hướng dẫn chi tiết
Bài tập 1. Cho hình chóp \(S.ABCD\) có đáy là hình thang vuông tại \(A\) và \(B\) có \(AD
= 2AB = 2CD = 2a\) và \(SA\bot(ABCD)\). Biết rằng \(SC\) tạo với đáy một góc \(60{^\circ}\). Tính tan góc giữa \(SA\) và các mặt phẳng \((SBC),(SCD)\) và \((SBD)\).
Bài tập 2. Cho hình chóp \(S.ABCD\), có đáy là nửa lục giác đều cạnh \(a\), \(AD = 2a\). Biết \(SA\bot(ABCD)\) và đường thẳng \(SB\) tạo với đáy một góc \(60{^\circ}\).
a) Tính tan góc tạo bởi \(SA\) và \((SBC)\).
b) Tính góc tạo bởi \(SA\)và \((SCD)\).
🔍 Để thuận tiện cho việc học tập và lưu trữ, mời bạn tải tài liệu tham khảo bên dưới.
---------------------------------------------
Khi nắm chắc phương pháp xác định góc giữa đường cao và mặt bên, học sinh sẽ giải quyết các bài toán góc trong không gian một cách tự tin và chính xác hơn. Những bài tập tính góc Toán 11 trong bài giúp củng cố kỹ năng, tránh nhầm lẫn và nâng cao khả năng vận dụng trong các dạng toán liên quan.
