Chứng minh hai đường thẳng vuông góc – Lý thuyết và bài tập vận dụng
Bài tập chứng minh hai đường thẳng vuông góc Toán 11
Trong hình học không gian Toán 11, dạng toán chứng minh hai đường thẳng vuông góc đóng vai trò nền tảng để giải quyết nhiều bài toán liên quan đến góc và khoảng cách. Tuy nhiên, nếu không nắm vững cơ sở lý thuyết và cách vận dụng, học sinh rất dễ suy luận thiếu chặt chẽ.
Bài viết này sẽ hệ thống lý thuyết chứng minh hai đường thẳng vuông góc, kết hợp bài tập vận dụng tiêu biểu, giúp người học hiểu đúng bản chất và áp dụng linh hoạt trong từng dạng bài.
A. Cách chứng minh hai đường thẳng vuông góc
Muốn chứng minh đường thẳng 
\(a\) vuông góc với đường thẳng \(b\), ta đi tìm mặt phẳng \((\beta)\) chứa đường thẳng \(b\) sao cho việc chứng minh \(a\bot(\beta)\) dễ thực hiện.
Mối quan hệ giữa song song và vuông góc: \(\left\{ \begin{matrix}
a//b \\
c\bot a
\end{matrix} \right.\ \overset{}{\rightarrow}c\bot b\)
B. Bài tập minh họa chứng minh hai đường thẳng vuông góc
Ví dụ 1. Cho hình chóp tứ giác đều \(S.ABCD\) có tất cả các cạnh bằng \(a\) (như hình vẽ)
Chứng minh hai đường thẳng \(SC\) và \(BD\) vuông góc với nhau?
Hướng dẫn giải
Gọi \(O\) là tâm của hình vuông \(ABCD.\)
Ta có \(S.ABCD\) là chóp đều \(\Rightarrow\) \(SO\bot(ABCD) \Rightarrow SO\bot BD.\) Mà \(BD\bot AC\) nên \(BD\bot(SAC)\)
\(\Rightarrow BD\bot SC.\)
Vậy góc giữa hai đường thẳng \(SC\) và \(BD\) bằng \(90{^\circ}.\)
Ví dụ 2. Cho hình lập phương \(ABCD.A'B'C'D'\). Tính góc giữa hai đường thẳng \(CD'\) và \(AC'\).
Hướng dẫn giải
Hình vẽ minh họa :
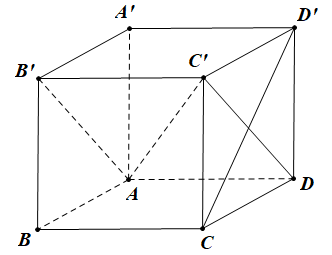
Ta có \(CD'\bot C'D\) (tính chất đường chéo hình vuông), \(CD'\bot
C'B'\) (tính chất hình lập phương).
Suy ra \(CD'\bot(AB'C'D)
\Rightarrow CD'\bot AC'\).
Vậy góc giữa hai đường thẳng \(CD'\) và \(AC'\) bằng \(90{^\circ}\).
Ví dụ 3. Cho hình chóp \(S.ABC\) có \(AB = AC\), \(\widehat{SAC} = \widehat{SAB}\). Chứng minh \(SA\) vuông góc với \(BC\).
Hướng dẫn giải
Hình vẽ minh họa:
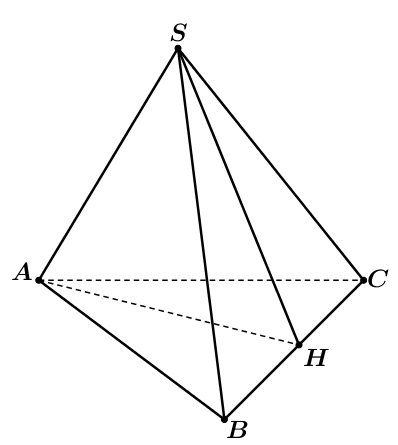
Vì \(AB = AC\), \(\widehat{SAC} = \widehat{SAB}\) nên \(\Delta SAC = \Delta SAB\), suy ra \(SB = SC\), nên hai tam giác \(ABC\) và \(SBC\) là tam giác cân.
Gọi \(H\) là trung điểm \(BC\), ta có
\(\left\{ \begin{matrix}
AH\bot BC \\
SH\bot BC
\end{matrix} \right.\ \Rightarrow (SAH)\bot BC\) nên \(SA\bot BC\) \(\Rightarrow (SA,BC) = 90{^\circ}\).
Vậy \(SA\bot BC\).
C. Bài tập tự rèn luyện có đáp án chi tiết
Bài tập 1. Cho hình hộp \(ABCD.MNPQ\) có sáu mặt đều là các hình vuông. Gọi \(E\), \(F\) lần lượt là trung điểm của \(AB\) và \(BC\).
a) Chứng minh: \(EF\bot BD\), \(EF\bot AM\).
b) Tính góc giữa \(EF\) và \(AQ\).
Bài tập 2: Cho hình chóp \(S.ABC\) có \(SA = SB = SC\) và \(\widehat{ASB} = \widehat{BSC} =
\widehat{CSA}\). Chứng minh rằng \(SA\bot BC\), \(SB\bot AC\) và \(SC\bot AB\).
Bài tập 3. Cho hình chóp \(S.ABCD\) có đáy là hình vuông \(ABCD\) cạnh bằng \(a\) và các cạnh bên đều bằng \(a\). Gọi \(M\) và \(N\) lần lượt là trung điểm của \(AD\) và \(SD\). Số đo của góc \((MN,SC)\) bằng bao nhiêu?
Bài tập 4. Cho tứ diện đều \(ABCD\). Chứng minh các cặp cạnh đối diện của tứ diện này vuông góc với nhau từng đôi một.
Bài tập 5. Hình chóp \(S.ABCD\) có cạnh \(SA\) vuông góc với mặt phẳng \((ABCD)\) và đáy \(ABCD\) là hình thang vuông tại \(A\) và \(D\) với \(AD = CD
= \frac{AB}{2}\).
a) Gọi \(I\) là trung điểm của đoạn \(AB\). Chứng minh \(CI\bot AB\) và \(DI\bot SC\).
📚 Phần tiếp theo của tài liệu đã được tổng hợp trong file đính kèm, mời bạn tải về để đọc tiếp.
------------------------------
Việc nắm chắc quan hệ vuông góc giữa hai đường thẳng trong không gian sẽ giúp học sinh xử lý chính xác các bài toán hình học không gian ở chương trình Toán 11. Thông qua hệ thống bài tập chứng minh hai đường thẳng vuông góc, người học có thể củng cố lý thuyết, rèn kỹ năng lập luận và nâng cao khả năng vận dụng vào các bài toán nâng cao.
