Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

Đóng

Điểm danh hàng ngày

Hôm nay +3
Ngày 2 +3
Ngày 3 +3
Ngày 4 +3
Ngày 5 +3
Ngày 6 +3
Ngày 7 +5

Bạn đã điểm danh Hôm nay và nhận 3 điểm! Đăng nhập ngay để nhận điểm

Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169

VnDoc.com

Cách xác định góc giữa hai đường thẳng nhanh và chính xác

Phương pháp giải bài toán 11 có ví dụ minh họa

Bài trước

Tải về

Bài sau

Lớp: Lớp 11

Môn: Toán

Dạng tài liệu: Chuyên đề

Loại: Tài liệu Lẻ

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Bài tập góc giữa hai đường thẳng trong không gian

A. Hướng dẫn xác định góc giữa hai đường thẳng trong không gian
B. Bài tập minh họa tính góc giữa hai đường thẳng
C. Bài tập tự rèn luyện có hướng dẫn đáp án chi tiết

Trong hình học không gian lớp 11, xác định góc giữa hai đường thẳng là dạng toán quen thuộc nhưng đòi hỏi cách dựng và lựa chọn phương pháp hợp lý để tránh nhầm lẫn. Nhiều học sinh mất nhiều thời gian do chưa nắm được hướng tiếp cận ngắn gọn và chính xác.

Bài viết này sẽ trình bày cách xác định góc giữa hai đường thẳng nhanh và chính xác, kèm ví dụ minh họa cụ thể, giúp người học áp dụng hiệu quả khi giải bài tập.

A. Hướng dẫn xác định góc giữa hai đường thẳng trong không gian

Để tính số đo của góc giữa hai đường thẳng $\left( d_{1} \right)$ $\left( d_{1} \right)$ và $\left( d_{2} \right)$ $\left( d_{2} \right)$ ta có thể thực hiện tính thông qua góc giữa hai đường thẳng cắt nhau lần lượt song song với hai đường thẳng đã cho.

Bước 1: Sử dụng tính chất sau: $\left\{ \begin{matrix} \left( d_{1},d_{2} \right) = \alpha \\ d_{2}//d_{3} \end{matrix} \right.\ \Rightarrow \left( d_{1},d_{2} \right) = \left( d_{1},d_{3} \right) = \alpha$ $\left\{ \begin{matrix} \left( d_{1},d_{2} \right) = \alpha \\ d_{2}//d_{3} \end{matrix} \right.\ \Rightarrow \left( d_{1},d_{2} \right) = \left( d_{1},d_{3} \right) = \alpha$
Bước 2: Áp dụng định lí côsin trong tam giác để xác định góc.

Để tính góc giữa hai đường thẳng trong không gian ta cần nhớ các công thức sau:

Định lý cosin trong tam giác $ABC$:

$\cos\widehat{BAC} = \frac{AB^{2} + AC^{2} - BC^{2}}{2.AB.AC}$ $\cos\widehat{BAC} = \frac{AB^{2} + AC^{2} - BC^{2}}{2.AB.AC}$

$\cos\widehat{ABC} = \frac{BA^{2} + BC^{2} - AC^{2}}{2.BA.BC}$ $\cos\widehat{ABC} = \frac{BA^{2} + BC^{2} - AC^{2}}{2.BA.BC}$

$\cos\widehat{ACB} = \frac{CA^{2} + CB^{2} - AB^{2}}{2.CA.CB}$ $\cos\widehat{ACB} = \frac{CA^{2} + CB^{2} - AB^{2}}{2.CA.CB}$

B. Bài tập minh họa tính góc giữa hai đường thẳng

Ví dụ 1: Cho hình chóp $S.ABC$có đáy là tam giác đều cạnh $a$, $SA\bot(ABC)$ $SA\bot(ABC)$và $SA = a\sqrt{3}$ $SA = a\sqrt{3}$. Gọi $M$, $N$lần lượt là trung điểm $AB$và $SC$. Tính cosin của góc giữa hai đường thẳng $AN$và $CM$.

Hướng dẫn giải

Hình vẽ minh họa:

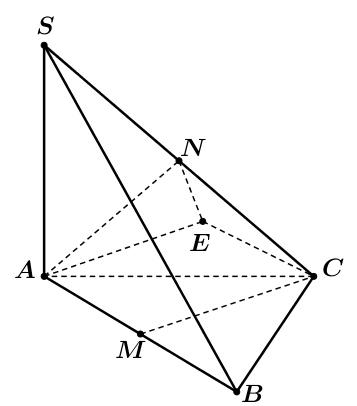
Dựng hình bình hành $AMCE$ suy ra $AM = CE = \frac{a}{2}$ $AM = CE = \frac{a}{2}$.

Khi đó $AE//CM \Rightarrow \left( \widehat{AN;CM} \right) = \left( \widehat{AN;AE} \right) = \varphi$ $AE//CM \Rightarrow \left( \widehat{AN;CM} \right) = \left( \widehat{AN;AE} \right) = \varphi$.

Mặt khác $SC = \sqrt{SA^{2} + AC^{2}} = 2a \Rightarrow AN = \frac{SC}{2} = a \Leftarrow AE = CM = \frac{a\sqrt{3}}{2}$ $SC = \sqrt{SA^{2} + AC^{2}} = 2a \Rightarrow AN = \frac{SC}{2} = a \Leftarrow AE = CM = \frac{a\sqrt{3}}{2}$.

Do $\Delta ABC$ $\Delta ABC$ đều nên $CM\bot AM$ $CM\bot AM$ $\Rightarrow AMCE$ $\Rightarrow AMCE$là hình chữ nhật.

Khi đó $CE\bot AE$ $CE\bot AE$ mà $CE\bot SA \Rightarrow CE\bot(SAE) \Rightarrow CE\bot SE$ $CE\bot SA \Rightarrow CE\bot(SAE) \Rightarrow CE\bot SE$.

Tam giác $\Delta SEC$ $\Delta SEC$ vuông tại $E$ có đường trung tuyến $EN = \frac{1}{2}SC = a$ $EN = \frac{1}{2}SC = a$.

Ta có:

$\cos\widehat{NAE} = \frac{AN^{2} + AE^{2} - NE^{2}}{2.AN.AE} = \frac{\sqrt{3}}{4} > 0 \Rightarrow \cos\varphi = \frac{\sqrt{3}}{4}$ $\cos\widehat{NAE} = \frac{AN^{2} + AE^{2} - NE^{2}}{2.AN.AE} = \frac{\sqrt{3}}{4} > 0 \Rightarrow \cos\varphi = \frac{\sqrt{3}}{4}$.

Ví dụ 2. Cho tứ diện $ABCD$ có $AB$ vuông góc với mặt phẳng $(BCD)$. Biết tam giác $BCD$ vuông tại $C$ và $AB = \frac{a\sqrt{6}}{2},AC = a\sqrt{2},CD = a$ $AB = \frac{a\sqrt{6}}{2},AC = a\sqrt{2},CD = a$. Gọi $E$ là trung điểm của $AC$ (tham khảo hình vẽ bên).

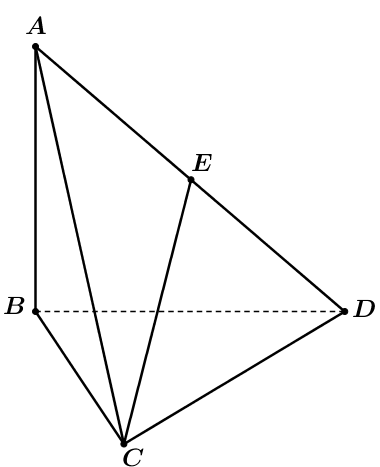
Tính góc giữa hai đường thẳng $AB$ và $CE$.

Hướng dẫn giải

Hình vẽ minh họa:

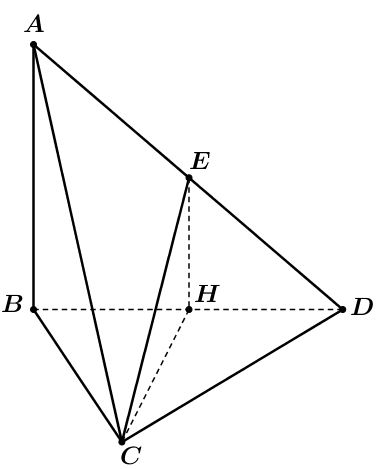
Gọi $H$ là trung điểm $BD$ $\Rightarrow EH//AB \Rightarrow EH\bot(BCD)$ $\Rightarrow EH//AB \Rightarrow EH\bot(BCD)$

Vậy $EH\bot CH$ $EH\bot CH$, ta có $BC = \sqrt{AC^{2} - AB^{2}} = \frac{a\sqrt{2}}{2}$ $BC = \sqrt{AC^{2} - AB^{2}} = \frac{a\sqrt{2}}{2}$

Suy ra $BD = \sqrt{BC^{2} + CD^{2}} = \frac{a\sqrt{6}}{2} \Rightarrow CH = \frac{BD}{2} = \frac{a\sqrt{6}}{4}$ $BD = \sqrt{BC^{2} + CD^{2}} = \frac{a\sqrt{6}}{2} \Rightarrow CH = \frac{BD}{2} = \frac{a\sqrt{6}}{4}$

Lại có $EH = \frac{AB}{2} = \frac{a\sqrt{6}}{4} = CH$ $EH = \frac{AB}{2} = \frac{a\sqrt{6}}{4} = CH$

$\Rightarrow \Delta EHC$ $\Rightarrow \Delta EHC$ vuông cân tại $H$

Do đó $\widehat{(AB;CE)} = \widehat{(EH;CE)} = \widehat{CEH} = 45{^\circ}$ $\widehat{(AB;CE)} = \widehat{(EH;CE)} = \widehat{CEH} = 45{^\circ}$.

Ví dụ 3. Cho hình chóp $S.ABCD$ có đáy là hình vuông $ABCD$ cạnh $2a$, $SA\bot(ABCD)$ $SA\bot(ABCD)$ và $SB = a\sqrt{5}$ $SB = a\sqrt{5}$. Gọi $M$là trung điểm $AB$ và $N$ là trung điểm $BC$. Tính cosin góc giữa hai đường thẳng $SM$và $DN$.

Hướng dẫn giải

Hình vẽ minh họa:

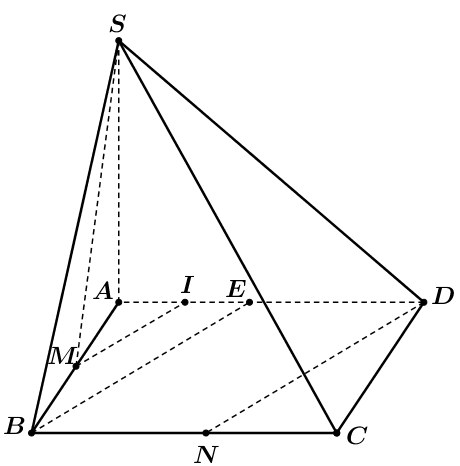
Do $SA\bot(ABCD)$ $SA\bot(ABCD)$.

Ta có: $SA = \sqrt{SB^{2} - AB^{2}} = a$ $SA = \sqrt{SB^{2} - AB^{2}} = a$.

Gọi $E$ là trung điểm của $AD$ và $I$ là trung điểm $AE$.

Dễ thấy $BNDE$ là hình bình hành và $MI$là đường trung bình trong tam giác $ABE$.

Khi đó:$DN//BE//MI$ nên ta có: $AM = a;\ AI = \frac{AE}{2} = \frac{a}{2}$ $AM = a;\ AI = \frac{AE}{2} = \frac{a}{2}$.

Mặt khác: $SM^{2} = SA^{2} + AM^{2} = 2a^{2};\ SI^{2} = \frac{5a^{2}}{4}$ $SM^{2} = SA^{2} + AM^{2} = 2a^{2};\ SI^{2} = \frac{5a^{2}}{4}$

$\Rightarrow MI^{2} = AI^{2} + AM^{2} = \frac{5a^{2}}{4}$ $\Rightarrow MI^{2} = AI^{2} + AM^{2} = \frac{5a^{2}}{4}$.

Do vậy $\cos\widehat{SMI} = \frac{SM^{2} + MI^{2} - SI^{2}}{2.SM.MI} = \frac{\sqrt{10}}{5} = \cos\widehat{(SM;DN)}$ $\cos\widehat{SMI} = \frac{SM^{2} + MI^{2} - SI^{2}}{2.SM.MI} = \frac{\sqrt{10}}{5} = \cos\widehat{(SM;DN)}$

C. Bài tập tự rèn luyện có hướng dẫn đáp án chi tiết

Bài tập 1. Cho hình chóp $S.ABC$ có $SA = SB = SC = AB = a;\ AC = a\sqrt{2}$ $SA = SB = SC = AB = a;\ AC = a\sqrt{2}$ và $BC = a\sqrt{3}$ $BC = a\sqrt{3}$. Tính cosin góc giữa hai đường thẳng $SC$ và $AB$.

Bài tập 2: Cho hình chóp $S.ABCD$ có đáy $ABCD$là hình chữ nhật có $AB = a;AD = a\sqrt{2}$ $AB = a;AD = a\sqrt{2}$, $SA\bot(ABCD)$ $SA\bot(ABCD)$ và $SA = 2a$.

a) Tính cosin góc giữa hai đường thẳng $BC$ và $SD$.

b) Gọi $I$là trung điểm của $CD$. Tính cosin góc giữa hai đường thẳng $SB$và $AI$.

Bài tập 3: Cho hình chóp $S.ABCD$ có đáy là hình thoi cạnh $a$, $\widehat{ABC} = 60^{0}$ $\widehat{ABC} = 60^{0}$. Tam giác $SAB$cân tại $S$và thuộc mặt phẳng vuông góc với đáy. Biết rằng $SC$ tạo với đáy một góc $30{^\circ}$ $30{^\circ}$. Tính cosin của góc giữa

a) $SD$ và $BC$.

b) $DH$ và $SC$ với $H$ là chân đường cao hạ từ $S$xuống mặt đáy $(ABCD)$.

Bài tập 4: Cho hình chóp $S.ABCD$ có đáy là hình thang vuông tại $A$ và $B$ có $AD = 2AB$ $= 2CD = 2a$ và $SA\bot(ABCD)$ $SA\bot(ABCD)$. Biết rằng $SC$tạo với đáy một góc $60^{0}$ $60^{0}$. Tính cosin góc giữa:

a) $BC$ và $SD$.

b) $AI$ và $SD$ với $I$ là trung điểm $CD$.

🔍 Để thuận tiện cho việc học tập và lưu trữ, mời bạn tải tài liệu tham khảo bên dưới.

-----------------------------

Khi nắm vững phương pháp xác định góc giữa hai đường thẳng, học sinh sẽ giải quyết bài toán hình học không gian một cách chủ động và hiệu quả hơn. Những ví dụ minh họa Toán 11 trong bài giúp củng cố bản chất vấn đề, tạo nền tảng vững chắc để xử lý các dạng bài nâng cao liên quan đến góc trong không gian.

Xem thử Tải về

Chọn file muốn tải về: