Cách chứng minh hai mặt phẳng vuông góc
Quan hệ vuông góc trong không gian Toán 11
Trong hình học không gian Toán 11, dạng toán chứng minh hai mặt phẳng vuông góc giữ vai trò then chốt khi giải các bài toán về góc và quan hệ không gian. Nếu không nắm vững tiêu chí và cách lập luận, học sinh rất dễ nhầm lẫn giữa các mối quan hệ song song – vuông góc.
Bài viết này sẽ trình bày cách chứng minh hai mặt phẳng vuông góc một cách rõ ràng, giúp người học hiểu đúng bản chất và áp dụng hiệu quả trong quá trình làm bài.
A. Hai mặt phẳng vuông góc
Để chứng minh hai mặt phẳng ![]() \((P)\) và
\((P)\) và ![]() \((Q)\) vuông góc với nhau ta sẽ chứng minh:
\((Q)\) vuông góc với nhau ta sẽ chứng minh:
-
Một đường thẳng
 \(d\) nằm trong mặt phẳng
\(d\) nằm trong mặt phẳng  \((P)\) vuông góc với mặt phẳng
\((P)\) vuông góc với mặt phẳng  \((Q)\) hoặc ngược lại, một đường thẳng nào đó nằm trong mặt phẳng
\((Q)\) hoặc ngược lại, một đường thẳng nào đó nằm trong mặt phẳng  \((Q)\) và vuông góc với mặt phẳng
\((Q)\) và vuông góc với mặt phẳng  \((P).\)
\((P).\) -
Góc giữa hai mặt phẳng
 \((P)\) và
\((P)\) và  \((Q)\) bằng
\((Q)\) bằng  \(90^{0}\).
\(90^{0}\).
B. Bài tập minh họa chứng minh hai mặt phẳng vuông góc
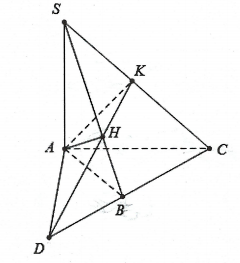
Ví dụ 1: Cho hình chóp ![]() \(S.ABC\) có đáy là tam giác
\(S.ABC\) có đáy là tam giác ![]() \(ABC\) vuông tại
\(ABC\) vuông tại ![]() \(B\) và
\(B\) và ![]() \(SA\bot(ABC).\)
\(SA\bot(ABC).\)
a) Chứng minh ![]() \((SBC)\bot(SAB).\)
\((SBC)\bot(SAB).\)
b) Gọi ![]() \(AH\) và
\(AH\) và ![]() \(AK\) lần lượt là đường cao trong tam giác
\(AK\) lần lượt là đường cao trong tam giác ![]() \(SAB\) và
\(SAB\) và ![]() \(SAC.\) Chứng minh
\(SAC.\) Chứng minh ![]() \((SBC)\bot(AKH).\)
\((SBC)\bot(AKH).\)
c) Gọi ![]() \(D\) là giao điểm của
\(D\) là giao điểm của ![]() \(HK\) và
\(HK\) và ![]() \(BC.\) Chứng minh rằng
\(BC.\) Chứng minh rằng ![]() \((SAD)\bot(SAC).\)
\((SAD)\bot(SAC).\)
Hướng dẫn giải
Hình vẽ minh họa:
a) Do ![]() \(SA\bot(ABC) \Rightarrow SA\bot
BC.\)
\(SA\bot(ABC) \Rightarrow SA\bot
BC.\)
Tam giác ![]() \(ABC\) vuông tại
\(ABC\) vuông tại ![]() \(B\) nên
\(B\) nên ![]() \(AB\bot
BC.\)
\(AB\bot
BC.\)
Do đó ![]() \(BC\bot(SAB) \Rightarrow
(SBC)\bot(SAB).\)
\(BC\bot(SAB) \Rightarrow
(SBC)\bot(SAB).\)
b) Ta có: ![]() \(BC\bot(SAB) \Rightarrow BC\bot
AH\) mà
\(BC\bot(SAB) \Rightarrow BC\bot
AH\) mà ![]() \(AH\bot SC\)
\(AH\bot SC\)
![]() \(\Rightarrow AH\bot(SBC) \Rightarrow
(AHK)\bot(SBC).\)
\(\Rightarrow AH\bot(SBC) \Rightarrow
(AHK)\bot(SBC).\)
c) Ta có: ![]() \(AH\bot(SBC) \Rightarrow AH\bot
SC\)
\(AH\bot(SBC) \Rightarrow AH\bot
SC\)
Mặt khác ![]() \(AK\bot SC \Rightarrow
SC\bot(AHK)\) hay
\(AK\bot SC \Rightarrow
SC\bot(AHK)\) hay ![]() \(SC\bot(AKD).\)
\(SC\bot(AKD).\)
Suy ra ![]() \(AD\bot SC\) mà
\(AD\bot SC\) mà ![]() \(SA\bot AD \Rightarrow AD\bot(SAC).\)
\(SA\bot AD \Rightarrow AD\bot(SAC).\)
Do vậy ![]() \((SAD)\bot(SAC).\)
\((SAD)\bot(SAC).\)
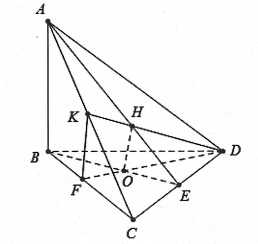
Ví dụ 2: Cho tứ diện ![]() \(ABCD\) có cạnh
\(ABCD\) có cạnh ![]() \(AB\) vuông góc với mặt phẳng
\(AB\) vuông góc với mặt phẳng ![]() \((BCD).\) Trong tam giác
\((BCD).\) Trong tam giác ![]() \(BCD\) vẽ các đường cao
\(BCD\) vẽ các đường cao ![]() \(BE\) và
\(BE\) và ![]() \(DF\) cắt nhau tại
\(DF\) cắt nhau tại ![]() \(O.\) Trong mặt phẳng
\(O.\) Trong mặt phẳng ![]() \((ACD)\) vẽ
\((ACD)\) vẽ ![]() \(DK\) vuông góc với
\(DK\) vuông góc với ![]() \(AC\) tại
\(AC\) tại ![]() \(K.\) Gọi
\(K.\) Gọi ![]() \(H\) là trực tâm của tam giác
\(H\) là trực tâm của tam giác ![]() \(ACD.\)
\(ACD.\)
a) Chứng minh mặt phẳng ![]() \((ADC)\) vuông góc với mặt phẳng
\((ADC)\) vuông góc với mặt phẳng ![]() \((ABE)\) và mặt phẳng
\((ABE)\) và mặt phẳng ![]() \((ADC)\) vuông góc với mặt phẳng
\((ADC)\) vuông góc với mặt phẳng ![]() \((DFK).\)
\((DFK).\)
b) Chứng minh rằng ![]() \(OH\) vuông góc với mặt phẳng
\(OH\) vuông góc với mặt phẳng ![]() \((ACD).\)
\((ACD).\)
Hướng dẫn giải
Hình vẽ minh họa:
a) Ta có: ![]() \(\left\{ \begin{matrix}
BE\bot CD \\
AB\bot CD
\end{matrix} \right.\ \Rightarrow CD\bot(ABE)\) mà
\(\left\{ \begin{matrix}
BE\bot CD \\
AB\bot CD
\end{matrix} \right.\ \Rightarrow CD\bot(ABE)\) mà ![]() \(CD \subset (ACD)\)
\(CD \subset (ACD)\)
![]() \(\Rightarrow (ADC)\bot(ABE).\)
\(\Rightarrow (ADC)\bot(ABE).\)
Lại có: ![]() \(\left\{ \begin{matrix}
DF\bot BC \\
DF\bot AB
\end{matrix} \right.\ \Rightarrow DF\bot(ABC) \Rightarrow DF\bot
AC.\)
\(\left\{ \begin{matrix}
DF\bot BC \\
DF\bot AB
\end{matrix} \right.\ \Rightarrow DF\bot(ABC) \Rightarrow DF\bot
AC.\)
Mặt khác: ![]() \(DK\bot AC \Rightarrow
AC\bot(DKF)\)
\(DK\bot AC \Rightarrow
AC\bot(DKF)\)
![]() \(\Rightarrow (ACD)\bot(DFK).\)
\(\Rightarrow (ACD)\bot(DFK).\)
b) Do ![]() \(CD\bot(ABE) \Rightarrow CD\bot
AE.\)
\(CD\bot(ABE) \Rightarrow CD\bot
AE.\)
Ta có:  \(\left\{ \begin{matrix}
(ACD)\bot(ABE) \\
(ACD)\bot(DFK) \\
OH = (ABE) \cap (DFK)
\end{matrix} \right.\ \Rightarrow OH\bot(ACD).\)
\(\left\{ \begin{matrix}
(ACD)\bot(ABE) \\
(ACD)\bot(DFK) \\
OH = (ABE) \cap (DFK)
\end{matrix} \right.\ \Rightarrow OH\bot(ACD).\)
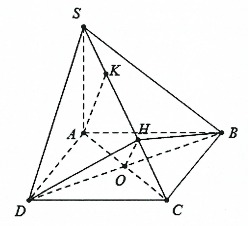
Ví dụ 3: Cho hình chóp ![]() \(S.ABCD\) có đáy
\(S.ABCD\) có đáy ![]() \(ABCD\) là hình thoi tâm
\(ABCD\) là hình thoi tâm ![]() \(O\) cạnh
\(O\) cạnh ![]() \(a\) và
\(a\) và ![]() \(BD =
a.\) Biết cạnh
\(BD =
a.\) Biết cạnh ![]() \(SA =\frac{a \sqrt{6}}{2}\) và vuông góc với mặt phẳng
\(SA =\frac{a \sqrt{6}}{2}\) và vuông góc với mặt phẳng ![]() \((ABCD).\) Chứng minh rằng:
\((ABCD).\) Chứng minh rằng:
a) ![]() \((SAC)\bot(SBD).\) b)
\((SAC)\bot(SBD).\) b) ![]() \((SCD)\bot(SBC).\)
\((SCD)\bot(SBC).\)
Hướng dẫn giải
Hình vẽ minh họa:
a) Do ![]() \(SA\bot(ABCD) \Rightarrow SA\bot
BD.\)
\(SA\bot(ABCD) \Rightarrow SA\bot
BD.\)
Mặt khác ![]() \(ABCD\) là hình thoi nên
\(ABCD\) là hình thoi nên ![]() \(AC\bot BD.\)
\(AC\bot BD.\)
Do đó ![]() \(BD\bot(SAC) \Rightarrow
(SBD)\bot(SAC).\)
\(BD\bot(SAC) \Rightarrow
(SBD)\bot(SAC).\)
b) Dựng ![]() \(OH\bot SC\).
\(OH\bot SC\).
Do ![]() \(BD\bot(SAC) \Rightarrow BD\bot
SC\) suy ra
\(BD\bot(SAC) \Rightarrow BD\bot
SC\) suy ra ![]() \(SC\bot(DHB).\)
\(SC\bot(DHB).\)
Như vậy ![]() \(\widehat{DHB}\) là góc giữa hai mặt phẳng
\(\widehat{DHB}\) là góc giữa hai mặt phẳng ![]() \((SCD)\) và
\((SCD)\) và ![]() \((SBC).\)
\((SBC).\)
Tam giác ![]() \(ABD\) đều cạnh
\(ABD\) đều cạnh ![]() \(a\) nên
\(a\) nên ![]() \(AO =
\frac{a\sqrt{3}}{2} \Rightarrow AC = a\sqrt{3}.\)
\(AO =
\frac{a\sqrt{3}}{2} \Rightarrow AC = a\sqrt{3}.\)
Dựng ![]() \(AK\bot SC\)
\(AK\bot SC\)
![]() \(\Rightarrow AK =
\frac{SA.OC}{\sqrt{SA^{2} + OC^{2}}} = a\)
\(\Rightarrow AK =
\frac{SA.OC}{\sqrt{SA^{2} + OC^{2}}} = a\)
![]() \(\Rightarrow OH = \frac{AK}{2} =
\frac{a}{2}.\)
\(\Rightarrow OH = \frac{AK}{2} =
\frac{a}{2}.\)
Tam giác ![]() \(DHB\) có đường trung tuyến
\(DHB\) có đường trung tuyến ![]() \(HO = \frac{1}{2}BD =
\frac{a}{2}\)
\(HO = \frac{1}{2}BD =
\frac{a}{2}\)
![]() \(\Rightarrow \Delta DHB\) vuông tại
\(\Rightarrow \Delta DHB\) vuông tại ![]() \(H\) hay
\(H\) hay ![]() \(\widehat{DHB} = 90^{o}.\)
\(\widehat{DHB} = 90^{o}.\)
Do đó ![]() \((SCD)\bot(SBC).\)
\((SCD)\bot(SBC).\)
C. Bài tập tự rèn luyện có hướng dẫn giải chi tiết
Bài tập 1. Cho hình chóp ![]() \(S.ABCD\) có đáy
\(S.ABCD\) có đáy ![]() \(ABCD\) là hình chữ nhật, biết
\(ABCD\) là hình chữ nhật, biết ![]() \(AB = a,\ \ AD = a\sqrt{2},\ \ SA =
a\) và
\(AB = a,\ \ AD = a\sqrt{2},\ \ SA =
a\) và ![]() \(SA\bot(ABCD).\) Gọi
\(SA\bot(ABCD).\) Gọi ![]() \(M\) là trung điểm của
\(M\) là trung điểm của ![]() \(AD,\)
\(AD,\) ![]() \(I\) là giao điểm của
\(I\) là giao điểm của ![]() \(BM\) và
\(BM\) và ![]() \(AC.\) Chứng minh rằng
\(AC.\) Chứng minh rằng ![]() \((SAC)\bot(SMB).\)
\((SAC)\bot(SMB).\)
Bài tập 2. Cho hình chóp ![]() \(S.ABCD\) có đáy
\(S.ABCD\) có đáy ![]() \(ABCD\) là hình vuông cạnh
\(ABCD\) là hình vuông cạnh ![]() \(2a,\) tam giác
\(2a,\) tam giác ![]() \(SAB\) cân tại
\(SAB\) cân tại ![]() \(S\) và nằm trong mặt phẳng vuông góc với đáy. Gọi
\(S\) và nằm trong mặt phẳng vuông góc với đáy. Gọi ![]() \(H\) là trung điểm của
\(H\) là trung điểm của ![]() \(AB.\) Biết
\(AB.\) Biết ![]() \(SA =
SB = a\sqrt{2}.\)
\(SA =
SB = a\sqrt{2}.\)
a) Chứng minh rằng ![]() \(SH\bot(ABCD).\)
\(SH\bot(ABCD).\)
b) Chứng minh tam giác ![]() \(SBC\) vuông.
\(SBC\) vuông.
c) Chứng minh ![]() \((SAD)\bot(SAB);\ \
(SAD)\bot(SBC).\)
\((SAD)\bot(SAB);\ \
(SAD)\bot(SBC).\)
✨ Bài viết chỉ trích dẫn một phần nội dung, mời bạn tải tài liệu đầy đủ để nắm trọn kiến thức.
---------------------------------------
Việc nắm chắc phương pháp chứng minh hai mặt phẳng vuông góc sẽ giúp học sinh xử lý chính xác nhiều dạng bài toán hình học không gian ở chương trình Toán 11. Khi hiểu rõ bản chất của quan hệ vuông góc giữa các mặt phẳng, người học sẽ chủ động hơn trong việc phân tích và giải các bài toán nâng cao.










