Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

Đóng

Điểm danh hàng ngày

Hôm nay +3
Ngày 2 +3
Ngày 3 +3
Ngày 4 +3
Ngày 5 +3
Ngày 6 +3
Ngày 7 +5

Bạn đã điểm danh Hôm nay và nhận 3 điểm! Đăng nhập ngay để nhận điểm

Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169

VnDoc.com

Xác định thiết diện của hình chóp và lăng trụ khi cắt bởi mặt phẳng

Bài tập Toán 11 có đáp án

Bài trước

Tải về

Bài sau

Lớp: Lớp 11

Môn: Toán

Dạng tài liệu: Chuyên đề

Loại: Tài liệu Lẻ

Mức độ: Trung bình

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Hướng dẫn giải bài toán thiết diện Toán 11

A. Các bước xác định giao tuyến và thiết diện
B. Bài tập minh họa xác định và tính diện tích thiết diện
C. Bài tập tự rèn luyện có hướng dẫn chi tiết

Trong hình học không gian Toán 11, dạng toán xác định thiết diện của hình chóp và lăng trụ khi cắt bởi mặt phẳng là nội dung quan trọng, thường xuất hiện trong các bài kiểm tra và đề thi. Dạng bài này yêu cầu người học phải quan sát không gian tốt và lựa chọn đúng cách xác định giao tuyến của mặt phẳng cắt.

Bài viết sau sẽ hướng dẫn phương pháp xác định thiết diện của hình chóp và lăng trụ, kèm bài tập có đáp án, giúp học sinh hiểu rõ quy trình và vận dụng hiệu quả khi làm bài.

A. Các bước xác định giao tuyến và thiết diện

Giả sử thiết diện là một phần của mặt phẳng $(P)$ và $(P)\bot d$ $(P)\bot d$.
Khi đó ta tìm mặt trung gian $(\alpha)$ $(\alpha)$ dễ thấy và $(\alpha)\bot d \rightarrow (\alpha)\ //\ (P)$ $(\alpha)\bot d \rightarrow (\alpha)\ //\ (P)$ và quy về thiết diện có yếu tố song song đã biết.

B. Bài tập minh họa xác định và tính diện tích thiết diện

Ví dụ 1. Hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông tâm $O$ cạnh $a$, $SO\bot(ABCD),SO = \frac{a\sqrt{6}}{2}$ $SO\bot(ABCD),SO = \frac{a\sqrt{6}}{2}$. Mặt phẳng $(P)$ đi qua $A$ và vuông góc với $SC$. Xác định và tính diện tích thiết diện của $(P)$ với hình chóp.

Hướng dẫn giải

Hình vẽ minh họa:

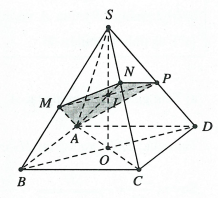
Kẻ $AN\bot SC(N \in SC)$ $AN\bot SC(N \in SC)$ và $AN \cap SO = I$ $AN \cap SO = I$

Ta có $BD\bot(SAC) \Rightarrow BD\bot SC$ $BD\bot(SAC) \Rightarrow BD\bot SC$, qua $I$ kẻ đường thẳng $d$ song song với $BD$ cắt $SB,SC$ lần lượt tại $M,P \Rightarrow mp(P) \equiv (AMNP)$ $M,P \Rightarrow mp(P) \equiv (AMNP)$.

Suy ra mp $(P)$ cắt khối chóp theo thiết diện là tứ giác $AMNP.$

Tam giác $SAO$ có $SA = \sqrt{SO^{2} + OA^{2}} = a\sqrt{2} = AC$ $SA = \sqrt{SO^{2} + OA^{2}} = a\sqrt{2} = AC$

$\Rightarrow$ $\Rightarrow$ Tam giác $SAC$ đều $\Rightarrow$ $\Rightarrow$ N là trung điểm của $SC \Rightarrow$ $SC \Rightarrow$ $I$ là trọng tâm tam giác $SAC \Rightarrow \frac{MP}{BD} = \frac{SI}{SO} = \frac{2}{3} \Rightarrow MP = \frac{2a\sqrt{2}}{3}$ $SAC \Rightarrow \frac{MP}{BD} = \frac{SI}{SO} = \frac{2}{3} \Rightarrow MP = \frac{2a\sqrt{2}}{3}$.

Vậy diện tích tứ giác $AMNP$ là

$S_{AMNP} = \frac{1}{2}MP.AN = \frac{1}{2}.\frac{2a\sqrt{2}}{3}.\frac{a\sqrt{6}}{2} = \frac{a^{2}\sqrt{3}}{3}$ $S_{AMNP} = \frac{1}{2}MP.AN = \frac{1}{2}.\frac{2a\sqrt{2}}{3}.\frac{a\sqrt{6}}{2} = \frac{a^{2}\sqrt{3}}{3}$.

Ví dụ 2. Cho tứ diện $ABCD$ có $\Delta BCD$ $\Delta BCD$ đều, gọi $BH$là đường cao của $\Delta BCD$ $\Delta BCD$, $O$ là trung điểm của $BH$ và $AO\bot(BCD),AO = BH = 2a$ $AO\bot(BCD),AO = BH = 2a$, trên $OH$ lấy điểm $I$ sao cho $BI = x(a < x < 2a)$, mặt phẳng $(\alpha)$ $(\alpha)$ đi qua $I$ và vuông góc $OH$. Dựng và tính diện tích thiết diện của tứ diện tạo bởi $(\alpha)$ $(\alpha)$.

Hướng dẫn giải

Hình vẽ minh họa:

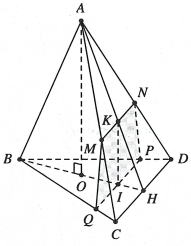
Vì $AO\bot(BCD) \Rightarrow AO\bot OH$ $AO\bot(BCD) \Rightarrow AO\bot OH$

Qua $I$ kẻ $IK\ //\ AH(K \in AH)$ $IK\ //\ AH(K \in AH)$.

Tam giác $BCD$ đều $\Rightarrow BH\bot CD$ $\Rightarrow BH\bot CD$, qua $K$ kẻ đường thẳng $d$song song với đường thẳng $CD$ cắt $SC,SD$ lần lượt tại $M,N.$

Qua $I$ kẻ đường thẳng $\Delta$ $\Delta$ song song với đường thẳng $CD$ cắt $BC,BD$ lần lượt tại $Q,P.$

Suy ra mặt phẳng $(\alpha)$ $(\alpha)$ cắt khối chóp theo thiết diện là tứ giác $MNPQ.$

Diện tích hình thang $MNPQ$ là $S_{MNPQ} = \frac{1}{2}IK.(MN + PQ)$ $S_{MNPQ} = \frac{1}{2}IK.(MN + PQ)$.

Tam giác $BCD$ có: $\frac{PQ}{CD} = \frac{BI}{BH} \Rightarrow PQ = \frac{x}{2a}.\frac{4a\sqrt{3}}{3} = \frac{2x\sqrt{3}}{3}$ $\frac{PQ}{CD} = \frac{BI}{BH} \Rightarrow PQ = \frac{x}{2a}.\frac{4a\sqrt{3}}{3} = \frac{2x\sqrt{3}}{3}$.

Tam giác $ACD$ có: $\frac{MN}{CD} = \frac{AK}{AH} = \frac{OI}{OH} \Rightarrow MN = \frac{OI.CD}{OH} = \frac{4\sqrt{3}}{3}(x - a)$ $\frac{MN}{CD} = \frac{AK}{AH} = \frac{OI}{OH} \Rightarrow MN = \frac{OI.CD}{OH} = \frac{4\sqrt{3}}{3}(x - a)$.

Tam giác $AHO$ có: $\frac{IK}{AO} = \frac{IH}{OH} \Rightarrow IK = \frac{IH.AO}{OH} = 2(2a - x)$ $\frac{IK}{AO} = \frac{IH}{OH} \Rightarrow IK = \frac{IH.AO}{OH} = 2(2a - x)$.

Vậy diện tích hình thang $MNPQ$ là:

$S = \frac{1}{2}.2(2a - x)\left( \frac{2x\sqrt{3}}{3} + \frac{4\sqrt{3}}{3}(x - a) \right) = \frac{2\sqrt{3}}{3}(2a - x)(3x - 2a)$ $S = \frac{1}{2}.2(2a - x)\left( \frac{2x\sqrt{3}}{3} + \frac{4\sqrt{3}}{3}(x - a) \right) = \frac{2\sqrt{3}}{3}(2a - x)(3x - 2a)$.

C. Bài tập tự rèn luyện có hướng dẫn chi tiết

Bài tập 1. Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$, các cạnh bên đều bằng $\frac{a\sqrt{3}}{2}$ $\frac{a\sqrt{3}}{2}$. Gọi $I$ là trung điểm của $BC$, $(\alpha)$ $(\alpha)$ là mặt phẳng qua $A$ và vuông góc với $SI$. Hãy xác định thiết diện của hình chóp với mặt phẳng $(\alpha)$ $(\alpha)$.

Bài tập 2. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$ có $SA$vuông góc với đáy, $SA = a\sqrt{2}$ $SA = a\sqrt{2}$. Kẻ $AH$ vuông góc với $SB.$

a) Chứng minh $\frac{SH}{SB} = \frac{2}{3}$ $\frac{SH}{SB} = \frac{2}{3}$.

b) Mặt phẳng $(P)$ qua $A$ vuông góc với $SB$ cắt $SC$ tại $M.$Tìm thiết diện của hình chóp cắt bởi $(P)$ và tính thiết diện đó.

Bài tập 3. Cho hình chóp $S.ABCD$ có đáy là hình thang vuông tại $A$ và $D.$ Cạnh $AB = 2a$, $AD = DC = a$, $SA\bot(ABCD),SA = a$ $SA\bot(ABCD),SA = a$.

a) Chứng minh $(SBC)\bot(SAC)$ $(SBC)\bot(SAC)$.

b) Gọi $(\alpha)$ $(\alpha)$ là mặt phẳng chứa $SD$ và vuông góc với mặt phẳng$(SAC)$. Xác định thiết diện của hình chóp cắt bởi $(\alpha)$ $(\alpha)$. Tính diện tích thiết diện ấy.

c) Mặt phẳng $(\beta)$ $(\beta)$ đi qua trung điểm $M$ của $SA$ và $N \in AD$ $N \in AD$, $AN = x(0 < x < a)$, vuông góc với $(SAD)$. Xác định và tính diện tích thiết diện của hình chóp với mặt phẳng $(\beta)$ $(\beta)$ theo $a$ và $x$.

📖 Toàn bộ nội dung, bài tập và lời giải đã được tổng hợp trong tài liệu tải về.

===================================

Việc nắm vững cách xác định thiết diện trong hình chóp và lăng trụ sẽ giúp học sinh tiếp cận bài toán không gian một cách chủ động và chính xác hơn. Thông qua hệ thống bài tập Toán 11 có đáp án, người học có thể rèn luyện kỹ năng dựng hình, củng cố tư duy không gian và nâng cao khả năng giải các dạng bài thiết diện thường gặp.

Xem thử Tải về

Chọn file muốn tải về: