Đề thi thử Đại học năm 2013 - môn Toán khối A (THPT chuyên Hà Nội - Amsterdam)

Đề thi đại học môn Toán

PHẦN CHUNG CHO TẤT CẢ THÍ SINH (7 điểm)

Câu I (2 điểm) Cho hàm số y = x³ - 3x² + 3mx + 1 - m có đồ thị (C_m)

1. Khảo sát sự biến thiên và vẽ đồ thị hàm số khi m = 0.

2. Tìm các giá trị của tham số m để hàm số có cực trị, đồng thời đường thẳng đi qua hai điểm cực trị tạo với đường thẳng ∆: 3x + y - 8 = 0 một góc 45⁰.

Câu II (2 điểm)

1. Giải phương trình: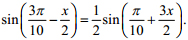

2. Tìm các giá trị của m để phương trình: 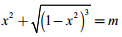có nghiệm trên R.

Câu III (1 điểm)

Tính tích phân: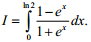

Câu IV (1 điểm)

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a, AD = 2a, cạnh SA vuông góc với đáy, cạnh SB lập với đáy một góc 60⁰. Trên cạnh SA lấy điểm M với 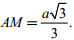Mặt phẳng (BCM) cắt cạnh SD tại N. Tính khoảng cách giữa hai đường thẳng AB, SC và tính thể tích khối chóp S.BCNM.

Câu V (1 điểm) Cho các số dương x, y, z thỏa mãn: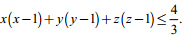

Tìm giá trị nhỏ nhất của: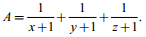

PHẦN RIÊNG (3 điểm): Thí sinh chỉ làm một trong hai phần (Phần A hoặc phần B)

A. Theo chương trình chuẩn

Câu VI.a (2 điểm)

1. Trong mặt phẳng Oxy cho tam giác ABC vuông cân tại A. Biết rằng cạnh huyền nằm trên đường thẳng d: x + 7y - 31 = 0, điểm N(1; 5/2) thuộc đường thẳng AC, điểm M (2; -3) thuộc đường thẳng AB. Xác định tọa độ các đỉnh của tam giác ABC.

2. Trong không gian tọa độ Oxyz cho hình lăng trụ đứng tam giác ABC.A'B'C' với A(0; -3; 0), B(4; 0; 0), C(0; 3; 0), B'(4; 0; 4). Gọi M là trung điểm của A'B'. Mặt phẳng P đi qua hai điểm A, M và song song với BC', (P) cắt A'C' tại điểm N. Tính độ dài đoạn MN.

Câu VII.a (1 điểm) Tìm số phức z thỏa mãn hai điều kiện: 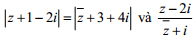là một số thuần ảo.

B. Theo chương trình nâng cao

Câu VI.b (2 điểm)

1. Trong mặt phẳng tọa độ Oxy cho đường tròn (C): x² + y² - 2x + 4y + 2 = 0. Gọi (C') là đường tròn có tâm I(5; 1) và cắt đường tròn (C) tại 2 điểm M, N sao cho 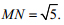. Hãy viết phương trình của (C')

2. Trong không gian tọa độ Oxyz cho hình lập phương ABCD.A'B'C'D' các đỉnh A(0; 0; 0), B(1; 0; 0), D(0; 1; 0) và A'(0; 0; 1). Gọi (P) là mặt phẳng thay đổi, luôn chứa đường thẳng CD', α là góc giữa mặt phẳng (P) và mặt phẳng BB'D'D. Tìm giá trị nhỏ nhất của α.

Câu VII. b (1 điểm) Giải hệ phương trình: