Phép thử và biến cố trong xác suất lớp 11: Định nghĩa và ứng dụng

Phép thử và biến cố là những khái niệm cơ bản nhưng vô cùng quan trọng trong chương trình xác suất lớp 11. Hiểu rõ định nghĩa và cách áp dụng phép thử, biến cố giúp học sinh dễ dàng giải quyết các bài toán xác suất phức tạp và xây dựng nền tảng vững chắc cho các môn học nâng cao. Bài viết này sẽ cung cấp cho bạn cái nhìn tổng quan về phép thử và biến cố trong xác suất, cùng các ví dụ minh họa và ứng dụng thực tế để nắm chắc kiến thức và tự tin hơn trong học tập.

1. Phép thử

Phép thử ngẫu nhiên là phép thử mà ta không đoán trước được kết quả của nó, mặc dù đã biết tập hợp tất cả các kết quả có thể có của phép thử đó.

2. Không gian mẫu

Tập hợp các kết quả có thể xảy ra của một phép thử được gọi là không gian mẫu của phép thử và kí hiệu là $\mathrm{\Omega }$

3. Biến cố

Biến cố là một tập con của không gian mẫu.

Ví dụ 1. Gieo một đồng tiền hai lần. Phép thử này có không gian mẫu là $\mathrm{\Omega }=\{SS,SN,NS,NN\}$. Khi tiến hành phép thử, sự kiện A : “kết quả của hai lần gieo là khác nhau” có thể xảy ra. Ta viết $A=\{SN,NS\}$ và A được gọi là biến cố.

Rõ ràng $A\subset \mathrm{\Omega }$

Biến cố không thể là biến cố không bao giờ xảy ra. Tập $\varnothing$ được gọi là biến không thể (gọi tắt là biến cố không).

Tập $\mathrm{\Omega }$ được gọi là biến cố chắc chắn.

Ví dụ 2. Gieo một con súc sắc. Gọi sự kiện B : “con súc sắc xuất hiện mặt 9 chấm”

Biến cố B không xảy ra nên $B=\varnothing$

Chú ý. Mỗi kết quả của phép thử làm cho biến cố A xảy ra được gọi là một kết quả thuận lợi cho A. Tập hợp các kết quả thuận lợi cho A được kí hiệu ${\mathrm{\Omega }}_A$ hoặc n(A)

4. Phép toán trên các biến cố

a. Biến cố đối

Tập $\mathrm{\Omega }\mathrm{\setminus }A$ được gọi là biến cố đối của biến cố A, kí hiệu $\bar{A}$

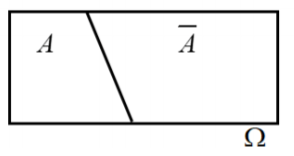
b. Các phép toán

Giả sử A và B là hai biến cố liên quan đến một phép thử. Ta có:

• Tập $A\cup B$ được gọi hợp của hai biến cố A và B
• Tập $A\cap B$ được gọi giao của hai biến cố A và B, $A\cap B$ có thể viết là $A.B$
• Nếu $A\cap B=\varnothing$ thì ta nói A và B xung khắc, suy ra $B\subset \bar{A}$( $\bar{A}$ là biến cố đối của A).

Một số lưu ý:

Khi tiếp cận các khái niệm mới trong phần này, một vấn đề thường gặp là các em chưa biệt sâu sắc được hai khái niệm biến đối và biến cố xung khắc. Để nhớ chắc thì các em cần lưu ý diễn đạt bằng hình vẽ ở hình vẽ trên.

Hai biến cố đối nhau cũng là hai biến cố xung khắc, hai biến cố xung khắc chưa chắc là hai biến cố đối nhau

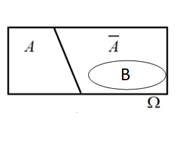
Trong hình vẽ: $A,\bar{A}$ là hai biến cố đối cũng là hai biến cố xung khắc vì $A\cap \bar{A}=\varnothing$

$A$ và$B$ là hai biến cố xung khắc.

-------------------------------------------

Nắm bắt chính xác định nghĩa và ứng dụng của phép thử và biến cố trong xác suất lớp 11 không chỉ giúp bạn làm tốt bài tập mà còn mở rộng khả năng tư duy logic trong toán học. Hãy vận dụng những kiến thức đã học để giải quyết các bài toán xác suất một cách linh hoạt và hiệu quả. Chúc bạn học tốt và thành công trên con đường chinh phục môn xác suất!