Bài tập đổi đơn vị góc lượng giác
Cách đổi đơn vị góc từ radian sang độ, từ độ sang radian
Trong chương trình Toán 11, phần đổi đơn vị góc lượng giác là nền tảng quan trọng để học sinh làm chủ chương lượng giác, radian và các dạng toán liên quan. Đây cũng là dạng bài thường xuyên xuất hiện trong kiểm tra, thi học kỳ và đề thi đánh giá năng lực. Bài viết dưới đây tổng hợp đầy đủ bài tập đổi đơn vị góc lượng giác từ cơ bản đến nâng cao, kèm đáp án chi tiết giúp bạn rèn kỹ năng tính toán, tránh sai sót và nâng cao tốc độ làm bài.
A. CÔNG THỨC ĐỔI ĐƠN VỊ GÓC
Đổi từ độ sang rađian
Đổi từ rađian sang độ
\(\alpha rad = \alpha.\left(
\frac{180}{\pi} \right)^{0}\)
Ví dụ minh họa:
a. Đổi số đo của góc \(-
\frac{3\pi}{16}rad\) sang đơn vị độ?
b. Đổi số đo của góc \(40^{0}35'\) sang đơn vị radian với độ chính xác đến hàng phần trăm?
Hướng dẫn giải:
a. Áp dụng công thức ta có:
\(- \frac{3\pi}{16}rad = -
\frac{3\pi.180^{0}}{16.\pi} = \left( \frac{135}{6} \right)^{0} =
33,75^{0}\)
b. Áp dụng công thức \(\mu =
\frac{m.\pi}{180}\) với \(\mu\) tính bằng rad và \(m\) tính bằng độ.
Ta có: \(40^{0}35' = \left( 40 +
\frac{25}{60} \right)^{0}\) khi đó:
\(\mu = \frac{\left( 40 + \frac{25}{60}
\right).\pi}{180} = \frac{97.\pi}{432} \approx 0,71\)
B. BÀI TẬP VẬN DỤNG ĐỔI ĐƠN VỊ GÓC CÓ ĐÁP ÁN
Câu 1: Góc có số đo \(108^{0}\) đổi ra rađian là:
A. \(\frac{3\pi}{5}\) B. \(\frac{\pi}{10}\) C. \(\frac{3\pi}{2}\) D. \(\frac{\pi}{4}\)
Câu 2: Nếu một cung tròn có số đo là \(a^{0}\) thì số đo radian của nó là:
A. \(180\pi a\) B. \(\frac{180\pi}{a}\) C. \(\frac{a\pi}{180}\). D. \(\frac{\pi}{180a}\).
Câu 3: Cho góc có số đo \(405^{\circ}\), khi đổi góc này sang đơn vị rađian ta được
A. \(\frac{8\pi}{9}\) B. \(\frac{9\pi}{4}\) C. \(\frac{9}{4}\) D. \(\frac{9\pi}{8}\)
Câu 4: Đổi số đo của góc \(10rad\) sang đơn vị độ, phút, giây ta được
A. \(572^{0}57'28\) B. \(1800^{0}\) C. \(\frac{\pi}{18}\) D. \(527^{\circ}57'28\)
Câu 5: Góc có số đo \(\frac{-
7\pi}{4}\) thì góc đó có số đo là
A. \(- 315^{0}\). B. \(- 630^{0}\). C. \(- 1^{0}45'\). D. \(- 135^{0}\).
Câu 6: Số đo theo đơn vị rađian của góc \(405^{\circ}\) là:
A. \(\frac{9\pi}{4}\). B. \(\frac{7\pi}{4}\). C. \(\frac{5\pi}{4}\). D. \(\frac{4\pi}{7}\).
Câu 7: Góc \(70^{0}\) có số đo bằng radian là:
A. \(\frac{18\pi}{7}\) B. \(\frac{7\pi}{18}\). C. \(\frac{9\pi}{7}\) D. \(\frac{7\pi}{9}\)
Câu 8: Góc có số đo \(120^{0}\) đổi sang radian là
A. \(\frac{3\pi}{2}\) B. \(\frac{2\pi}{3}\). C. \(\frac{\pi}{4}\). D. \(\frac{\pi}{10}\)
Câu 9: Góc lượng giác có số đo \(\alpha\) thì mọi góc lượng giác cùng tia đầu và tia cuối với nó có số đo dạng nào trong các dạng sau?
A. \(\alpha + k180^{0}\) B. \(\alpha + k360^{0}\). C. \(\alpha + k2\pi\). D. \(\alpha + k\pi\).
Câu 10: Trên đường tròn lượng giác như hình dưới.
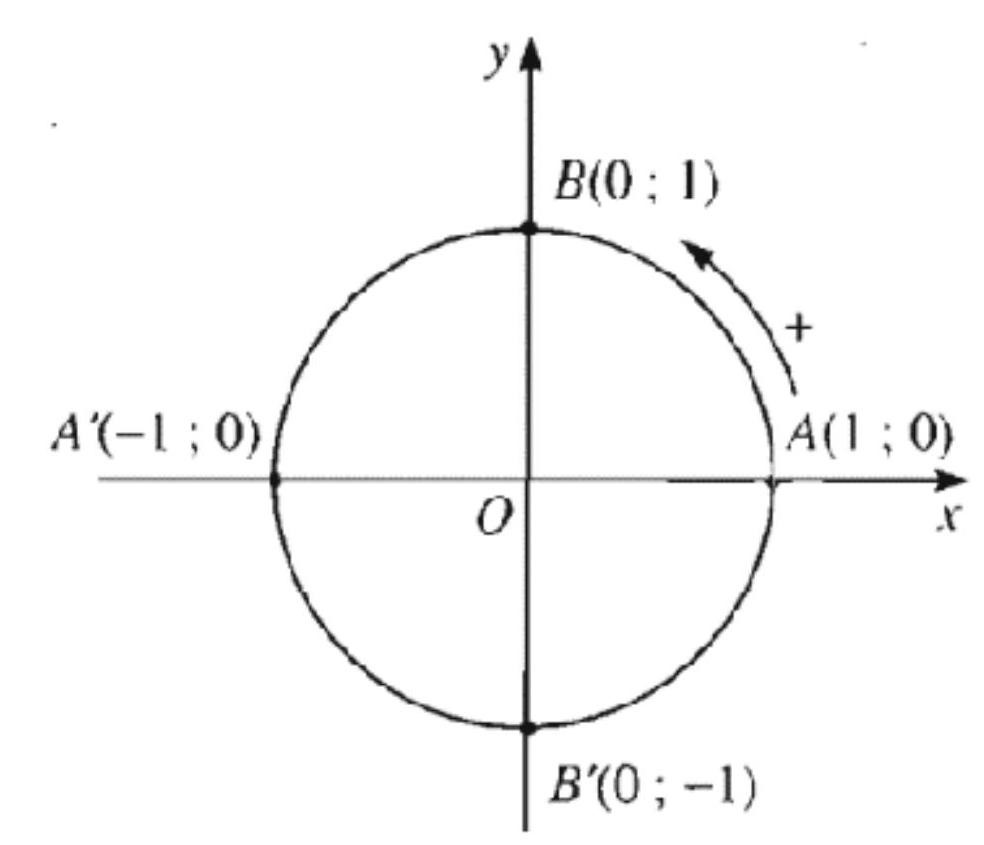
Số đo của góc lượng giác \((OA,OB')\) là
A. \(- \frac{\pi}{4}\) B. \(- \frac{\pi}{2}\) C. \(\frac{\pi}{4}\) D. \(\frac{\pi}{2}\)
Câu 11: Trên đường tròn lượng giác, cho góc lượng giác có số đo \(\frac{\pi}{2}(rad)\) thì mọi góc lượng giác có cùng tia đầu và tia cuối với góc lượng giác trên đều có số đo dạng:
A. \(\frac{\pi}{2}\). B. \(\frac{\pi}{2} + k\frac{\pi}{2},\left( k\mathbb{\in
Z} \right)\)
C. \(\frac{\pi}{2} +
k2\pi,\left( k \in \mathbb{Z} \right)\) D. \(\frac{\pi}{2} + k\pi,\left( k \in \mathbb{Z}
\right)\)
Câu 12: Kết quả nào sau đây là đúng?
A. \(1(rad) = 1^{0}\) B. \(1(rad) = \left( \frac{180}{\pi}
\right)^{0}\). C. \(1(rad) =
180^{0}\) D. \(1(rad) =
100^{0}\)
Toàn bộ nội dung đã sẵn sàng! Nhấn Tải về để tải đầy đủ tài liệu.
-------------------------------------
Thông qua hệ thống bài tập đổi đơn vị góc lượng giác và đáp án giải chi tiết, bạn có thể nắm vững cách chuyển đổi giữa độ – radian – grad, nhận biết quy luật tính nhanh và áp dụng linh hoạt trong các bài toán lượng giác lớp 11. Hãy luyện tập thường xuyên để nâng cao độ chính xác, củng cố kiến thức và tự tin đạt điểm cao trong các bài kiểm tra và kỳ thi quan trọng.
