Bài tập Đối xứng tâm: 20+ Câu trắc nghiệm cơ bản nhất

Bạn đang tìm bộ bài tập giúp nắm vững kiến thức đối xứng tâm trong chương trình Toán 11? Bài viết Bài Tập Đối Xứng Tâm: 20+ Câu Trắc Nghiệm Cơ Bản Nhất mang đến cho bạn tuyển tập câu hỏi chọn lọc, bám sát chương trình và có đáp án chi tiết. Mỗi bài tập được thiết kế giúp học sinh dễ dàng nhận diện quy tắc, áp dụng tính chất và rèn kỹ năng giải nhanh các dạng trắc nghiệm thường gặp. Đây là tài liệu lý tưởng cho ôn luyện tại nhà, kiểm tra 15 phút – 1 tiết hoặc luyện thi học kỳ.

A. ĐỀ BÀI TRẮC NGHIỆM

Câu 1: Cho hai điểm \(I(1;2)\) và \(M(3; - 1)\). Hỏi điểm \(M'\) có tọa độ nào sau đây là ảnh của \(M\) qua phép đối xứng tâm \(I\)?

A. \((2;1)\)     B. \(( - 1;5)\)     C. \(( - 1;3)\)     D. \((5; - 4)\)

Câu 2: Trong mặt phẳng \(Oxy\) cho đường thẳng \(d\) có phương trình \(x = 2\). Trong các đường thẳng sau đường thẳng nào là ảnh của \(d\) qua phép đối xứng tâm \(O\)?

A. \(x = - 2\)     B. \(y = 2\)     C. \(x = 2\)              D. \(y = - 2\)

Câu 3: Trong các mệnh đề sau mệnh đề nào đúng?

A. Qua phép đối xứng tâm không có điểm nào biến thành chính nó.

B. Qua phép đối xứng tâm có đúng một điểm biến thành chính nó.

C. Có phép đối xứng tâm có hai điểm biến thành chính nó.

D. Có phép đối xứng tâm có vô số điểm biến thành chính nó.

Câu 4: Trong mặt phẳng \(Oxy\), cho đường thẳng \(d\) có phương trình \(x - y + 4 = 0\). Hỏi trong các đường thẳng sau đường thẳng nào có thể biến thành \(d\) qua một phép đối xứng tâm?

A. \(2x + y - 4 = 0\)              B. \(x + y - 1 = 0\)    C. \(2x - 2y + 1 = 0\)            D. \(2x + 2y - 3 = 0\)

Câu 5: Hình gồm hai đường tròn phân biệt có cùng bán kính có bao nhiêu tâm đối xứng?

A. Không có.             B. Một.           C. Hai.          D. Ba.

Câu 6: Trong hệ trục tọa độ \(Oxy\) cho điểm \(I(a;b)\) . Nếu phép đối xứng tâm \(I\) biến điểm \(M(x;y)\) thành \(M'(x';y')\) thì ta có biểu thức:

A. \(\left\{ \begin{matrix} x' = a + x \\ y' = b + y \end{matrix} \right.\).        B. \(\left\{ \begin{matrix} x' = 2a - x \\ y' = 2b - y \end{matrix} \right.\).       C. \(\left\{ \begin{matrix} x' = a - x \\ y' = b - y \end{matrix} \right.\).     D. \(\left\{ \begin{matrix} x = 2x' - a \\ y = 2y' - b \end{matrix} \right.\).

Câu 7: Trong mặt phẳng \(Oxy\), cho phép đối xứng tâm \(I(1;2)\) biến điểm \(M(x;y)\) thành \(M'(x';y')\). Khi đó:

A. \(\left\{ \begin{matrix} x' = - x + 2 \\ y' = - y - 2 \end{matrix} \right.\).     B. \(\left\{ \begin{matrix} x' = - x + 2 \\ y' = - y + 4 \end{matrix} \right.\) .    C. \(\left\{ \begin{matrix} x' = - x + 2 \\ y' = - y - 4 \end{matrix} \right.\) .     D. \(\left\{ \begin{matrix} x' = x + 2 \\ y' = y - 2 \end{matrix} \right.\).

Câu 8: Một hình \((H)\) có tâm đối xứng nếu và chỉ nếu:

A. Tồn tại phép đối xứng tâm biến hình \((H)\) thành chính nó.

B. Tồn tại phép đối xứng trục biến hình \((H)\) thành chính nó.

C. Hình \((H)\) là hình bình hành.

D. Tồn tại phép dời hình biến hình \((H)\) thành chính nó.

Câu 9: Hình nào sau đây không có tâm đối xứng?

A. Hình vuông.      B. Hình tròn.       C. Hình tam giác đều.      D. Hình thoi.

Câu 10: Trong mặt phẳng \((Oxy)\), tìm ảnh của điểm \(A(5;3)\) qua phép đối xứng tâm \(I(4;1)\).

A. \((5;3)\).      B. \(( - 5; - 3)\).      C. \((3; - 1)\).     D. \(\left( \frac{9}{2};2 \right)\).

Câu 11: Trong mặt phẳng \((Oxy)\) cho đường thẳng \(d\) có phương trình \(x + y - 2 = 0\), tìm phương trình đường thẳng \(d'\) là ảnh của \(d\) qua phép đối xứng tâm \(I(1;2)\).

A. \(x + y + 4 = 0\).      B. \(x + y - 4 = 0\).     C. \(x - y + 4 = 0\)           D. \(x - y - 4 = 0\).

Câu 12: Trong mặt phẳng \((Oxy)\), tìm phương trình đường tròn \((C')\) là ảnh của đường tròn \((C)\): \((x - 3)^{2} + (y + 1)^{2} = 9\) qua phép đối xứng tâm \(O(0;0)\).

A. \((x - 3)^{2} + (y + 1)^{2} = 9\).                B. \((x + 3)^{2} + (y + 1)^{2} = 9\).

C. \((x - 3)^{2} + (y - 1)^{2} = 9\).                 D. \((x + 3)^{2} + (y - 1)^{2} = 9\).

Câu 13: Tìm mệnh đề sai trong các mệnh đề sau:\({}_{}\)

A. Phép đối xứng tâm bảo toàn khoảng cách giữa 2 điểm bất kì.

B. Nếu \(IM' = IM\) thì \(D_{I}(M) = M'\).

C. Phép đối xứng tâm biến đường thẳng thành đường thẳng song song hoặc trùng với đường thẳng đã cho.

D. Phép đối xứng tâm biến tam giác bằng tam giác đã cho.

Câu 14: Trong mặt phẳng \((Oxy)\), cho điểm \(I\left( x_{0};y_{0} \right)\). Gọi \(M(x;y)\) là một điểm tùy ý và \(M'(x';y')\) là ảnh của \(M\) qua phép đối xứng tâm \(I\). Khi đó biểu thức tọa độ của phép đối xứng tâm \(I\) là:

A. \(\left\{ \begin{matrix} x' = 2x_{0} - x \\ y' = 2y_{0} - y \end{matrix} \right.\).      B. \(\left\{ \begin{matrix} x' = 2x_{0} + x \\ y' = 2y_{0} + y \end{matrix} \right.\).    C. \(\left\{ \begin{matrix} x = 2x_{0} + x' \\ y = 2y_{0} + y' \end{matrix} \right.\).     D. \(\left\{ \begin{matrix} x = x_{0} - x' \\ y = y_{0} - y' \end{matrix} \right.\).

Câu 15: Trong mặt phẳng \((Oxy)\), tìm phương trình đường tròn \((C')\) là ảnh của đường tròn \((C):\ x^{2} + y^{2} = 1\) qua phép đối xứng tâm \(I(1;0)\).

A. \((x - 2)^{2} + y^{2} = 1\).      B. \((x + 2)^{2} + y^{2} = 1\).

C. \(x^{2} + (y + 2)^{2} = 1\).      D. \(x^{2} + (y - 2)^{2} = 1\).

(Còn tiếp)

B. ĐÁP ÁN TRẮC NGHIỆM TỔNG QUAN

C. HƯỚNG DẪN GIẢI CHI TIẾT

Câu 1:

\(I\) là trung điểm của \(MM'\) nên ta chọn câu \(( - 1;5)\).

Câu 2:

Ảnh là một đường thẳng song song với \(d\) (vì tâm đối xứng \(O\) không thuộc \(d\)) nên ta chọn \(x = - 2\).

Câu 3:

Chọn “Qua phép đối xứng tâm có đúng một điểm biến thành chính nó”, vì phép đối xứng tâm chỉ giữ bất biến tâm đối xứng.

Câu 4:

Phép đối xứng tâm biến một đường thẳng thành đường thẳng song song hoặc trùng với đường thẳng ban đầu, nên ta chọn đáp án \(2x - 2y + 1 = 0\) vì chỉ có đường thẳng ở câu \(2x - 2y + 1 = 0\) mới song song với \(d\).

Câu 5:

Hình vẽ minh họa:

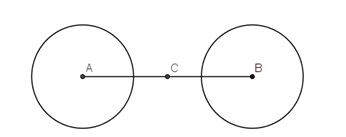
Hình gồm hai đường tròn phân biệt có cùng bán kính có một tâm đối xứng, tâm đối xứng đó chính là trung điểm của đoạn nối tâm.

Thật vậy, giả sử hai đường tròn là:

\(\begin{matrix} \left( C_{1} \right):\left( x - x_{1} \right)^{2} + \left( y - y_{1} \right)^{2} = R^{2}\ \ \ ; \\ \left( C_{2} \right):\left( x - x_{2} \right)^{2} + \left( y - y_{2} \right)^{2} = R^{2} \end{matrix}\)

Trung điểm đoạn nối tâm có tọa độ \(C\left( \frac{x_{1} + x_{2}}{2};\frac{y_{1} + y_{2}}{2} \right)\)

Lấy một điểm \(M\left( x_{0};y_{0} \right) \in \left( C_{1} \right) \Rightarrow \left( x_{0} - x_{1} \right)^{2} + \left( y_{0} - y_{1} \right)^{2} = R^{2}\)

Điểm đối xứng với \(M\) qua \(C\) có tọa độ \(M'\left( x_{1} + x_{2} - x_{0};y_{1} + y_{2} - y_{0} \right)\)

Ta chứng minh \(M' \in \left( C_{2} \right)\) do \(\left( x_{1} + x_{2} - x_{0} - x_{2} \right)^{2} + \left( y_{1} + y_{2} - y_{0} - y_{2} \right)^{2} = \left( x_{0} - x_{1} \right)^{2} + \left( y_{0} - y_{1} \right)^{2} = R^{2}\)

Với mỗi điểm \(M\) xác đinh được điểm \(M'\) là duy nhất nên \(C\) là tâm đối xứng của hai đường tròn.

Câu 6:

Phép đối xứng tâm \(I\) biến điểm \(M(x;y)\) thành \(M'(x';y')\) thì \(I\) là trung điểm của \(MM'\)

\(\Rightarrow \left\{ \begin{matrix}\dfrac{x + x'}{2} = a \\\dfrac{y + y'}{2} = b\end{matrix} \right.\ \Rightarrow \left\{ \begin{matrix}x' = 2a - x \\y' = 2b - y\end{matrix} \right.\) .

Câu 7:

Phép đối xứng tâm \(I\) biến điểm \(M(x;y)\) thành \(M'(x';y')\) thì \(I\) là trung điểm của \(MM'\)

\(\Rightarrow \left\{ \begin{matrix}\dfrac{x + x'}{2} = 1 \\\dfrac{y + y'}{2} = 2\end{matrix} \right.\ \Rightarrow \left\{ \begin{matrix}x' = - x + 2 \\y' = - y + 4\end{matrix} \right.\).

Không thể hiển thị hết nội dung tại đây — bấm Tải về để lấy toàn bộ tài liệu.

----------------------------------

Với hơn 20 câu trắc nghiệm cơ bản và lời giải rõ ràng, bài viết giúp bạn hệ thống lại toàn bộ kiến thức về phép đối xứng tâm, tối ưu tốc độ làm bài và tăng độ chính xác trong mọi bài kiểm tra Toán 11. Nếu bạn thấy tài liệu hữu ích, đừng quên lưu lại và tiếp tục khám phá thêm nhiều chuyên đề khác để hoàn thiện toàn bộ phần Hình học 11. Chúc bạn học tốt và đạt điểm số cao trong kỳ thi sắp tới!