VnDoc.com

Đóng

Bạn đã dùng hết 1 lần làm bài Trắc nghiệm miễn phí. Mời bạn mua tài khoản VnDoc PRO để tiếp tục! Tìm hiểu thêm

Mua VnDoc PRO chỉ từ 79.000đ

Đóng

Bạn cần đăng nhập tài khoản Thành viên VnDoc để:

- Xem đáp án

- Nhận 1 lần làm bài trắc nghiệm miễn phí!

Đăng nhập

Trắc nghiệm Toán 11 Phép tịnh tiến (mức độ Thông Hiểu)

Bài tập Toán 11 Online có đáp án

Phép tịnh tiến mức độ Thông Hiểu - có đáp án

Phép tịnh tiến là một phần quan trọng trong chương trình Hình học Oxy lớp 11, đòi hỏi học sinh không chỉ ghi nhớ lý thuyết mà còn phải biết vận dụng vào bài toán thực tế. Bộ trắc nghiệm Toán 11 Phép tịnh tiến (mức độ Thông Hiểu) dưới đây được thiết kế nhằm giúp bạn rèn luyện khả năng phân tích, áp dụng công thức và xử lý các dạng bài nâng cao hơn mức nhận biết. Tất cả câu hỏi đều có đáp án chi tiết, hỗ trợ bạn luyện tập hiệu quả thông qua hệ thống Bài tập Toán 11 Online có đáp án, giúp cải thiện tốc độ và độ chính xác khi làm bài.

Thông hiểu

Bài kiểm tra này bao gồm 20 câu
Điểm số bài kiểm tra: 20 điểm
Xem lại kỹ lý thuyết trước khi làm bài
Chuẩn bị giấy và bút để nháp trước khi bắt đầu

00:00:00

Câu 1: Thông hiểu
Tìm ảnh của đường tròn
Cho $\overrightarrow{v\ }(3;3)$ và đường tròn $(C):x^{2} + y^{2} - 2x + 4y - 4 = 0$ . Ảnh của $(C)$ qua $T_{\overrightarrow{v\ }}$ là $(C')$ có phương trình
- A.
  $(x - 4)^{2} + (y - 1)^{2} = 9$ .
- B.
  $(x - 4)^{2} + (y - 1)^{2} = 4$ .
- C.
  $(x + 4)^{2} + (y + 1)^{2} = 9$ .
- D.
  $x^{2} + y^{2} + 8x + 2y - 4 = 0$ .
Hướng dẫn:
Ta có $(C):x^{2} + y^{2} - 2x + 4y - 4 = 0$

$\Leftrightarrow (x - 1)^{2} + (y + 2)^{2} = 9$ suy ra $R = 3;I(1; - 2)$ là bán kính và tâm của $(C)$ .

Gọi $(C')$ là đường tròn là ảnh của $(C)$ qua phép tịnh tiến $T_{\overrightarrow{v\ }}$ .

Ta có $R' = R = 3$ và ảnh của tâm $I$ chính là tâm $I'$ của $(C')$ .

Theo công thức phép tịnh tiến ta có $I'(4;1)$ .

Vậy $(C'):(x - 4)^{2} + (y - 1)^{2} = 9$ .
Câu 2: Thông hiểu
Tìm ảnh của đường tròn qua phép tịnh tiến
Trong mặt phẳng tọa độ $Oxy$ , ảnh của đường tròn $(C)$ : $(x + 1)^{2} + (y - 3)^{2} = 4$ qua phép tịnh tiến theo vectơ $\overrightarrow{v} = (3;2)$ là đường tròn có phương trình
- A.
  $(x + 2)^{2} + (y + 5)^{2} = 4$ .
- B.
  $(x - 1)^{2} + (y + 3)^{2} = 4$ .
- C.
  $(x + 4)^{2} + (y - 1)^{2} = 4$ .
- D.
  $(x - 2)^{2} + (y - 5)^{2} = 4$ .
Hướng dẫn:
Đường tròn $(C)$ có tâm $I( - 1;3)$ , bán kính $R = 2$ .

Phép tịnh tiến theo vectơ $\overrightarrow{v}$ biến đường tròn $(C)$ thành $(C')$ có tâm $I'$ và bán kính $R' = 2$ .

$\Rightarrow$ $T_{\overrightarrow{v}}(I) = I'(x';y') \Leftrightarrow \overrightarrow{II'} = \overrightarrow{v}$ .

Ta có: $\overrightarrow{II'} = \left( x' + 1;y' - 3 \right)$ ; $\overrightarrow{v}(3;2)$

$\Rightarrow \left\{ \begin{matrix} x' + 1 = 3 \\ y' - 3 = 2 \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} x' = 2 \\ y' = 5 \end{matrix} \right.$ .

Do đó phương trình của đường tròn $(C')$ : $(x - 2)^{2} + (y - 5)^{2} = 4$ .
Câu 3: Thông hiểu
Chọn phương án thích hợp
Cho tam giác $ABC$ , gọi $M,\ \ N,\ \ P$ lần lượt là trung điểm các cạnh $BC,\ \ CA,\ \ AB$ ; phép tịnh tiến theo vectơ $\overrightarrow{u}$ biến điểm $N$ thành điểm $P$ . Khi đó vectơ $\overrightarrow{u}$ được xác định như thế nào?
- A.
  $\overrightarrow{u} = \frac{1}{2}\overrightarrow{AB}$ .
- B.
  $\overrightarrow{u} = \overrightarrow{MC}$ .
- C.
  $\overrightarrow{u} = - \frac{1}{2}\overrightarrow{BC}$ .
- D.
  $\overrightarrow{u} = \frac{1}{2}\overrightarrow{BC}$ .
Hướng dẫn:
Hình vẽ minh họa

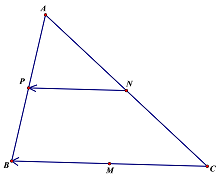
Vì $T_{\overrightarrow{u}}(N) = P$ nên $\overrightarrow{u} = \overrightarrow{NP} = - \frac{1}{2}\overrightarrow{BC}$ .
Câu 4: Thông hiểu
Tìm ảnh của đường thẳng qua phép tịnh tiến
Trong mặt phẳng tọa độ $Oxy$ cho đường thẳng $\Delta$ có phương trình $4x - y + 3 = 0$ . Ảnh của đường thẳng $\Delta$ qua phép tịnh tiến $T$ theo vectơ $\overrightarrow{v} = (2; - 1)$ có phương trình là
- A.
  $4x - y + 10 = 0$ .
- B.
  $4x - y - 6 = 0$ .
- C.
  $x - 4y - 6 = 0$ .
- D.
  $4x - y + 5 = 0$ .
Hướng dẫn:
Gọi đường thẳng $d$ là ảnh của đường thẳng $\Delta$ qua phép tịnh tiến $T$ theo vectơ $\overrightarrow{v} = (2; - 1)$ khi đó phương trình đường thẳng $d$ có dạng: $4x - y + m = 0$ .

Gọi $A(0;3)$ thuộc đường thẳng $d$ , $A'(x;y)$ là ảnh của điểm $A$ qua phép tịnh tiến $T$ khi đó $A' \in d$ .

Ta có $\overrightarrow{AA'} = \overrightarrow{v} \Rightarrow \left\{ \begin{matrix} x = 2 \\ y - 3 = - 1 \end{matrix} \right.$ $\Leftrightarrow \left\{ \begin{matrix} x = 2 \\ y = 2 \end{matrix} \right.\ \Rightarrow A'(2;2)$

Mà $A' \in d$ nên $8 - 2 + m = 0 \Leftrightarrow m = - 6$ nên phương trình đường thẳng $d$ là $4x - y - 6 = 0$ .
Câu 5: Thông hiểu
Tìm ảnh của đường tròn qua phép tịnh tiến
Cho $\overrightarrow{v}(3; - 2)$ và đường tròn $(C):x^{2} + y^{2} - 4x + 4y - 1 = 0$ . Ảnh của $(C)$ qua $T_{\overrightarrow{v}}$ là $(C')$ là:
- A.
  $(x - 5)^{2} + (y + 4)^{2} = 9$ .
- B.
  $(x + 5)^{2} + (y - 4)^{2} = 9$ .
- C.
  $x^{2} + y^{2} + 8x + 2y - 4 = 0$
- D.
  $(x + 1)^{2} + y^{2} = 9$ .
Hướng dẫn:
Đường tròn $(C):(x - 2)^{2} + (y + 2)^{2} = 9$ có tâm $I(2; - 2)$ .

Ta có $T_{\overrightarrow{v}}(I) = I'(5; - 4)$ . Đường tròn $(C')$ có cùng bán kính với $(C)$
Câu 6: Thông hiểu
Chọn kết luận đúng
Cho phép tịnh tiến vectơ $\overrightarrow{v}$ biến $A$ thành $A'$ và $M$ thành $M'$ . Khi đó:
- A.
  $3\overrightarrow{AM} = 2\overrightarrow{A'M'}$ .
- B.
  $\overrightarrow{AM} = - \overrightarrow{A'M'}$ .
- C.
  $\overrightarrow{AM} = 2\overrightarrow{A'M'}$ .
- D.
  $\overrightarrow{AM} = \overrightarrow{A'M'}$ .
Hướng dẫn:
Tính chất 1: Nếu $T_{\overrightarrow{v}}(M) = M';T_{\overrightarrow{v}}(N) = N'$ thì $\overrightarrow{M'N'} = \overrightarrow{MN}$ . Hay phép tịnh tiến bảo toàn khoảng cách giữa hai điểm bất kì.

Vậy đáp án cần tìm là: $\overrightarrow{AM} = \overrightarrow{A'M'}$ .
Câu 7: Thông hiểu
Tìm tọa độ vectơ
Trong mặt phẳng với hệ trục tọa độ Oxy, cho đường tròn $(C):(x - 1)^{2} + (y + 2)^{2} = 9$ và đường tròn $(C'):(x + 1)^{2} + (y - 3)^{2} = 9$ . Phép tịnh tiến theo vectơ $\overrightarrow{v}$ biến đường tròn $(C)$ thành đường tròn $(C')$ . Khi đó vectơ $\overrightarrow{v}$ có toạ độ là
- A.
  $\overrightarrow{v} = ( - 2;5)$ .
- B.
  $\overrightarrow{v} = (2; - 5)$ .
- C.
  $\overrightarrow{v} = (2;5)$ .
- D.
  $\overrightarrow{v} = (5;2)$ .
Hướng dẫn:
Đường tròn $(C)$ có tâm $I(1; - 2)$ và bán kính $R = 3$ , đường tròn $(C')$ có tâm $I'( - 1;3)$ và bán kính $R = 3$ .

Phép tịnh tiến theo véc tơ $\overrightarrow{v}$ biến đường tròn $(C)$ thành đường tròn $(C')$ thì $T_{\overrightarrow{v}}(I) = I'$

$\Leftrightarrow \overrightarrow{II'} = \overrightarrow{v} \Rightarrow \overrightarrow{v} = ( - 2;5)$ .
Câu 8: Thông hiểu
Viết phương trình đường thẳng d’ của d
Trong hệ tọa độ Oxy cho đường thẳng $d:x - 2y + 3 = 0$ . Phép tịnh tiến theo vectơ $\overrightarrow{u} =(2;2)$ biến đường thẳng d thành đường thẳng d' có phương trình là
- A.
  $2x - y + 5 = 0$
- B.
  $x - 2y + 4 = 0$
- C.
  $x + 2y + 5 = 0$
- D.
  $x - 2y + 5 = 0$
Hướng dẫn:
Ta có: $d':x - 2y + m = 0$

Gọi $A( - 3;0) \in d \Rightarrow A'( - 1;2) \in d' \Rightarrow m = 5$

Vậy đường thẳng d’ có phương trình $x - 2y + 5 = 0$ .
Câu 9: Thông hiểu
Chọn đáp án đúng
Trong mặt phẳng với hệ tọa độ $Oxy$ , cho véctơ $\overrightarrow{v} = (2;1)$ và điểm $A(4;5)$ . Hỏi $A$ là ảnh của điểm nào trong các điểm sau đây qua phép tịnh tiến theo $\overrightarrow{v}$ ?
- A.
  $B(6;6).$
- B.
  $I(2;4).$
- C.
  $D(1; - 1).$
- D.
  $C( - 2; - 4).$
Hướng dẫn:
Gọi $(x;y)$ là tọa độ tạo ảnh của điểm $A$ qua phép tịnh tiến theo $\overrightarrow{v}$ .

Khi đó: $\left\{ \begin{matrix} x = 4 - 2 = 2 \\ y = 5 - 1 = 4 \end{matrix} \right.$ .

Vậy điểm $A$ là ảnh của điểm $I(2;4)$ qua phép tịnh tiến theo $\overrightarrow{v}$
Câu 10: Thông hiểu
Chọn đáp án đúng
Trong mặt phẳng $Oxy$ cho điểm $A(2;5)$ . Hỏi $A$ là ảnh của điểm nào trong các điểm sau qua phép tịnh tiến theo vectơ $\overrightarrow{v} = (1;2)$ ?
- A.
  $(4;7)$ .
- B.
  $(1;3)$ .
- C.
  $(1;6)$ .
- D.
  $(3;1)$ .
Hướng dẫn:
$A$ là ảnh của điểm $M$ qua phép tịnh tiến theo vectơ $\overrightarrow{v} = (1;2)$

Áp dụng công thức biểu thức tọa dộ của phép tịnh tiến ta có:

$\left\{ \begin{matrix} x_{A} = x_{M} + a \\ y_{A} = y_{M} + b \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} x_{M} = 2 - 1 = 1 \\ y_{M} = 5 - 2 = 3 \end{matrix} \right.\ \Rightarrow M(1;3)$
Câu 11: Thông hiểu
Xác định vectơ
Trong mặt phẳng với hệ trục tọa độ $Oxy$ . Cho điểm $M( - 10;1)$ và $M'(3;8)$ . Phép tịnh tiến theo vectơ $\overrightarrow{v}$ biến điểm $M$ thành điểm $M'$ , khi đó tọa độ của vectơ $\overrightarrow{v}$ là ?
- A.
  $\overrightarrow{v} = ( - 13;7)$ .
- B.
  $\overrightarrow{v} = (13;7)$ .
- C.
  $\overrightarrow{v} = ( - 13; - 7)$ .
- D.
  $\overrightarrow{v} = (13; - 7)$ .
Hướng dẫn:
Phép tịnh tiến theo vecto $\overrightarrow{v}$ biến điểm $M$ thành điểm $M'$ nên ta có: $\overrightarrow{v} = \overrightarrow{MM'} = (13;7)$ .
Câu 12: Thông hiểu
Chọn kết luận đúng
Cho hai đường thẳng song song $d$ và $d'$ . Tất cả những phép tịnh tiến biến $d$ thành $d'$ là:
- A. Các phép tịnh tiến theo $\overrightarrow{AA'}$ , trong đó hai điểm $A$ và $A'$ tùy ý lần lượt nằm trên $d$ và $d'$ .
- B. Các phép tịnh tiến theo $\overrightarrow{v}$ , với mọi vectơ $\overrightarrow{v} \neq \overrightarrow{0}$ vuông góc với vectơ chỉ phương của $d$ .
- C. Các phép tịnh tiến theo $\overrightarrow{v}$ , với mọi vectơ $\overrightarrow{v} \neq \overrightarrow{0}$ tùy ý.
- D. Các phép tịnh tiến theo $\overrightarrow{v}$ , với mọi vectơ $\overrightarrow{v} \neq \overrightarrow{0}$ không song song với vectơ chỉ phương của $d$ .
Hướng dẫn:
Đáp án cần tìm là: Các phép tịnh tiến theo $\overrightarrow{AA'}$ , trong đó hai điểm $A$ và $A'$ tùy ý lần lượt nằm trên $d$ và $d'$
Câu 13: Thông hiểu
Tìm ảnh của đường thẳng d
Trong mặt phẳng tọa độ $Oxy$ , tìm ảnh của đường thẳng $d:x + 2y - 3 = 0$ qua phép tịnh tiến theo $\overrightarrow{v} = (1; - 1)$ .
- A.
  $d': - x + 2y + 2 = 0$ .
- B.
  $d':x + 2y - 4 = 0$ .
- C.
  $d':x + 2y - 2 = 0$ .
- D.
  $d':x - 2y - 4 = 0$ .
Hướng dẫn:
Ta có:

$T_{\overrightarrow{v}}(M) = M'(x';y')$

$\Leftrightarrow \left\{ \begin{matrix} x' = x + 1 \\ y' = y - 1 \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} x = x' - 1 \\ y = y' + 1 \end{matrix} \right.$

Mà: $M(x;y) \in d$

$\Rightarrow x' - 1 + 2\left( y' + 1 \right) - 3 = 0$

$\Leftrightarrow x' - 2y' - 2 = 0$ .

Vậy: $d': - x + 2y + 2 = 0$ .
Câu 14: Thông hiểu
Chọn kết luận đúng
Cho $P,Q$ cố định. Phép tịnh tiến T biến điểm $M$ bất kỳ thành $M_{2}$ sao cho $\overrightarrow{MM_{2}} = 2\overrightarrow{PQ}$ .
- A.
  T chính là phép tịnh tiến theo vectơ $\overrightarrow{MM_{2}}$ .
- B.
  T chính là phép tịnh tiến theo vectơ $\frac{1}{2}\overrightarrow{PQ}$ .
- C.
  T chính là phép tịnh tiến theo vectơ $2\overrightarrow{PQ}$ .
- D.
  T chính là phép tịnh tiến theo vectơ $\overrightarrow{PQ}$ .
Hướng dẫn:
Đáp án cần tìm là: T chính là phép tịnh tiến theo vectơ $2\overrightarrow{PQ}$ .
Câu 15: Thông hiểu
Chọn đáp án đúng
Trong mặt phẳng tọa độ $Oxy$ nếu phép tịnh tiến biến điểm $M(4;\ 2)$ thành điểm $M'(4;\ 5)$ thì nó biến điểm $A(2;\ 5)$ thành
- A.
  điểm $A'(2;\ 5)$ .
- B.
  điểm $A'(2;\ 8)$ .
- C.
  điểm $A'(5;\ 2)$ .
- D.
  điểm $A'(1;\ 6)$ .
Hướng dẫn:
Phép tịnh tiến biến điểm $M(4;\ 2)$ thành điểm $M'(4;\ 5)$ , biến điểm $A(2;\ 5)$ thành $A'(x;\ y)\ .$

$\Rightarrow \overrightarrow{M'A'} = \ \overrightarrow{MA}$ $\Leftrightarrow \left\{ \begin{matrix} x - 4 = 2 - 4 \\ y - 5 = 5 - 2 \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} x = 2 \\ y = 8 \end{matrix} \right.\ \ .$
Câu 16: Thông hiểu
Tìm tọa độ điểm M
Trong mặt phẳng tọa độ $Oxy$ cho $\overrightarrow{u} = (1; - 2)$ và điểm $M(2; - 3)$ . Ảnh của điểm $M$ qua phép tịnh tiến theo vectơ $\overrightarrow{u}$ là điểm có tọa độ nào trong các điểm sau?
- A.
  $M(1; - 1)$ .
- B.
  $M(1; - 3)$ .
- C.
  $M(3; - 5)$ .
- D.
  $M( - 2;3)$ .
Hướng dẫn:
Gọi $M(x;y)$ có ảnh qua phép tịnh tiến theo vectơ $\overrightarrow{u} = (a;b)$ là điểm $M'(x';y')$ .

Ta có $T_{\overrightarrow{u}}(M) = M' \Leftrightarrow \overrightarrow{MM'} = \overrightarrow{u} \Leftrightarrow \left\{ \begin{matrix} x' = x + a \\ y' = y + b \end{matrix} \right.$ .

Áp dụng công thức vào bài ta có tọa độ điểm $M'$ là ảnh của $M$ qua $T_{\overrightarrow{u}}$ là $M'(3; - 5)$ .
Câu 17: Thông hiểu
Chọn kết luận đúng
Cho phép tịnh tiến $T_{\overrightarrow{u}}$ biến điểm $M$ thành $M_{1}$ và phép tịnh tiến $T_{\overrightarrow{v}}$ biến $M_{1}$ thành $M_{2}$ .
- A.
  Một phép đối xứng trục biến $M$ thành $M_{2}$ .
- B.
  Không thể khẳng định được có hay không một phép dời hình biến $M$ thành $M_{2}$ _.
- C.
  Phép tịnh tiến $T_{\overrightarrow{u} + \overrightarrow{v}}$ biến $M$ thành $M_{2}$ .
- D.
  Phép tịnh tiến $T_{\overrightarrow{u} + \overrightarrow{v}}$ biến $M_{1}$ thành $M_{2}$ .
Hướng dẫn:
$T_{\overrightarrow{u}}$ biến điểm $M$ thành $M_{1}$ ta có $\overrightarrow{MM_{1}} = \overrightarrow{u}$

$T_{\overrightarrow{v}}$ biến $M_{1}$ thành $M_{2}$ ta có $\overrightarrow{M_{1}M_{2}} = \overrightarrow{v}$

Phép tịnh tiến $T_{\overrightarrow{u} + \overrightarrow{v}}$ biến $M$ thành $M_{2}$ khi đó

$\overrightarrow{u} + \overrightarrow{v} = \overrightarrow{MM_{2}} \Leftrightarrow \overrightarrow{MM_{1}} + \overrightarrow{M_{1}M_{2}} = \overrightarrow{MM_{2}}$

$\Leftrightarrow \overrightarrow{MM_{2}} = \overrightarrow{MM_{2}}$ (đúng)
Câu 18: Thông hiểu
Chọn đáp án đúng
Trong mặt phẳng $Oxy$ , ảnh của đường tròn : $(x + 1)^{2} + (y - 3)^{2} = 4$ qua phép tịnh tiến theo vectơ $\overrightarrow{v} = (3;2)$ là đường tròn có phương trình:
- A.
  $(x - 2)^{2} + (y - 5)^{2} = 4$ .
- B.
  $(x + 2)^{2} + (y + 5)^{2} = 4$ .
- C.
  $(x - 1)^{2} + (y + 3)^{2} = 4$ .
- D.
  $(x + 4)^{2} + (y - 1)^{2} = 4$ .
Hướng dẫn:
Theo định nghĩa ta có biểu thức tọa độ của phép tịnh tiến là :

$\left\{ \begin{matrix} x' = x + a = x + 3 \\ y' = y + b = y + 2\ \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} x = x' - 3 \\ y = y' - 2 \end{matrix} \right.$

Thay vào phương trình đường tròn ta có:

$(x + 1)^{2} + (y - 3)^{2} = 4$

$\Leftrightarrow \left( x' - 3 + 1 \right)^{2} + \left( y' - 2 - 3 \right)^{2} = 4$

$\Leftrightarrow (x' - 2)^{2} + (y' - 5)^{2} = 4$

Vậy ảnh của đường tròn : $(x + 1)^{2} + (y - 3)^{2} = 4$ qua phép tịnh tiến theo vectơ
$\overrightarrow{v} = (3;2)$ là đường tròn có phương trình: $(x - 2)^{2} + (y - 5)^{2} = 4$ .
Câu 19: Thông hiểu
Chọn đáp án đúng
Cho đường thẳng $d:2x - y + 1 = 0.$ Phép tịnh tiến theo $\overrightarrow{v}$ biến đường thẳng d thành chính nó. Tìm $\overrightarrow{v}$ ?
- A.
  $\overrightarrow{v} = ( - 1;2).$
- B.
  $\overrightarrow{v} = (2;1).$
- C.
  $\overrightarrow{v} = (2; - 1).$
- D.
  $\overrightarrow{v} = (1;2).$
Hướng dẫn:
Ta có:

$d:2x - y + 1 = 0$ suy ra VTPT của $d:\overrightarrow{n} = (2; - 1) \Rightarrow$ VTCP của $d:\overrightarrow{u} = (1;2)$ .

Để $T_{\overrightarrow{v}}(d) = d$ thì $\overrightarrow{v}$ cùng phương $\overrightarrow{u}$ .
Câu 20: Thông hiểu
Tìm câu sai
Một phép tịnh tiến biến điểm $A$ thành điểm $B$ và điểm $C$ thành điểm $D$ . Khẳng định nào sau đây là sai?
- A.
  Trung điểm của hai đoạn thẳng $AD$ và $BC$ trùng nhau.
- B.
  $\overrightarrow{AC} = \overrightarrow{BD}$ .
- C.
  $ABCD$ là hình bình hành.
- D.
  $\overrightarrow{AB} = \overrightarrow{CD}$ .
Hướng dẫn:
Phép tịnh tiến theo vectơ $\overrightarrow{v}$ biến điểm $A$ thành điểm $B \Leftrightarrow \overrightarrow{AB} = \overrightarrow{v}$ .

Phép tịnh tiến theo vectơ $\overrightarrow{v}$ biến điểm $C$ thành điểm $D \Leftrightarrow \overrightarrow{CD} = \overrightarrow{v}$ .

$\Rightarrow \overrightarrow{AB} = \overrightarrow{CD}$ nên “ $\overrightarrow{AB} = \overrightarrow{CD}$ ” đúng.

$\overrightarrow{AB} = \overrightarrow{CD} \Rightarrow$ tứ giác $ABDC$ là hình bình hành có hai đường chéo $AD$ và $BC$ cắt nhau tại trung điểm mỗi đường nê “Trung điểm của hai đoạn thẳng $AD$ và $BC$ trùng nhau” đúng.

$\overrightarrow{AB} = \overrightarrow{CD} \Leftrightarrow \overrightarrow{AC} + \overrightarrow{CB} = \overrightarrow{CB} + \overrightarrow{BD}$

$\Leftrightarrow \overrightarrow{AC} = \overrightarrow{BD}$ nên “ $\overrightarrow{AC} = \overrightarrow{BD}$ ” đúng.

Chia sẻ bởi:
Su kem

1

Tham khảo thêm

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!

Sắp xếp theo

Xóa Đăng nhập để Gửi

Lý thuyết Toán 11

Xem thêm

Mầm non

Lớp 1

Lớp 2

Lớp 3

Lớp 4

Lớp 5

Lớp 6

Lớp 7

Lớp 8

Lớp 9

Lớp 10

Lớp 11

Lớp 12

Thi vào lớp 6

Thi vào lớp 10

Thi Tốt Nghiệp THPT

Đánh Giá Năng Lực

Khóa Học Trực Tuyến

Hỏi bài

Trắc nghiệm Online

Tiếng Anh

Thư viện Học liệu

Bài tập Cuối tuần

Bài tập Hàng ngày

Thư viện Đề thi

Giáo án - Bài giảng

Tất cả danh mục

Trắc nghiệm Toán 11 Phép tịnh tiến (mức độ Thông Hiểu)

Phép tịnh tiến mức độ Thông Hiểu - có đáp án

Chúc mừng Bạn đã hoàn thành bài!

Tham khảo thêm

Tổng hợp lý thuyết phép đối xứng trục Toán 11

Tìm ảnh hay tạo ảnh của 1 đường tròn qua phép tịnh tiến (T)

Trọn bộ bài tập Phép tịnh tiến Toán 11 (Trắc nghiệm – Đáp án chuẩn)

Trắc nghiệm Toán 11 Phép tịnh tiến mức độ Nhận Biết

Lý thuyết Toán 11

Phép dời hình là gì? Khi nào hai hình được gọi là bằng nhau?

Trắc nghiệm Toán 11 Phép quay (mức độ nhận biết)

Tổng hợp bài tập Phép quay Toán 11 – Có đáp án và giải chi tiết

Phép quay là gì? Hiểu ngay với ví dụ Toán 11

Trắc nghiệm Toán 11 Phép quay (mức độ thông hiểu)

Trắc nghiệm Phép đối xứng trục Toán 11 – Có lời giải chi tiết