VnDoc.com

Trọn bộ bài tập Phép tịnh tiến Toán 11 (Trắc nghiệm – Đáp án chuẩn)

Chuyên đề Toán 11 có đáp án

Bài trước

Tải về

Bài sau

Lớp: Lớp 11

Môn: Toán

Dạng tài liệu: Chuyên đề

Loại: Tài liệu Lẻ

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Bộ bài tập trắc nghiệm phép tịnh tiến toán 11 có đáp án

Phép tịnh tiến là một trong những nội dung trọng tâm của hình học giải tích lớp 11, thường xuyên xuất hiện trong các bài kiểm tra và đề thi học kỳ. Để giúp học sinh nắm chắc kiến thức và rèn luyện kỹ năng làm bài, chúng tôi tổng hợp trọn bộ bài tập Phép tịnh tiến Toán 11 với đầy đủ dạng bài, câu hỏi trắc nghiệm và đáp án chi tiết – chuẩn xác. Bộ tài liệu được xây dựng bám sát chương trình Chuyên đề Toán 11, hỗ trợ bạn tự học hiệu quả, ghi nhớ nhanh công thức và nâng cao tốc độ xử lý bài tập.

A. ĐỀ BÀI TRẮC NGHIỆM

Câu 1. Mệnh đề nào sau đây là mệnh đề sai?

A. Phép tịnh tiến biến đoạn thẳng thành đoạn thẳng bằng nó.

B. Phép tịnh tiến biến đường tròn thành đường tròn có cùng bán kính.

C. Phép tịnh tiến biến đường thẳng thành đường thẳng song song với nó.

D. Phép tịnh tiến biến tam giác thành tam giác bằng nó.

Câu 2. Cho tam giác $ABC$, gọi $M,\ \ N,\ \ P$ $M,\ \ N,\ \ P$ lần lượt là trung điểm các cạnh $BC,\ \ CA,\ \ AB$ $BC,\ \ CA,\ \ AB$; phép tịnh tiến theo vectơ $\overrightarrow{u}$ $\overrightarrow{u}$ biến điểm $N$ thành điểm $P$. Khi đó vectơ $\overrightarrow{u}$ $\overrightarrow{u}$ được xác định như thế nào?

A. $\overrightarrow{u} = - \frac{1}{2}\overrightarrow{BC}$ $\overrightarrow{u} = - \frac{1}{2}\overrightarrow{BC}$. B. $\overrightarrow{u} = \overrightarrow{MC}$ $\overrightarrow{u} = \overrightarrow{MC}$. C. $\overrightarrow{u} = \frac{1}{2}\overrightarrow{AB}$ $\overrightarrow{u} = \frac{1}{2}\overrightarrow{AB}$. D. $\overrightarrow{u} = \frac{1}{2}\overrightarrow{BC}$ $\overrightarrow{u} = \frac{1}{2}\overrightarrow{BC}$.

Câu 3. Trong mặt phẳng tọa độ $Oxy$ cho các điểm $A( - 2;\ 5),\ A$ $A( - 2;\ 5),\ A'(4;\ 2),$ biết $A'$ là ảnh của $A$ qua phép tịnh tiến theo vectơ $\overrightarrow{u}$ $\overrightarrow{u}$ là

A. $\overrightarrow{u} = (1;\ 3)$ $\overrightarrow{u} = (1;\ 3)$. B. $\overrightarrow{u} = (6;\ - 3)$ $\overrightarrow{u} = (6;\ - 3)$. C. $\overrightarrow{u} = ( - 6;\ 3)$ $\overrightarrow{u} = ( - 6;\ 3)$. D. $\overrightarrow{u} = (2;\ - 1)$ $\overrightarrow{u} = (2;\ - 1)$.

Câu 4. Trong mặt phẳng $Oxy$, cho hai đường thẳng $\left( d_{1} \right):2x + 3y + 1 = 0$ $\left( d_{1} \right):2x + 3y + 1 = 0$và $\left( d_{2} \right):x - y - 2 = 0$ $\left( d_{2} \right):x - y - 2 = 0$. Có bao nhiêu phép tịnh tiến biến $d_{1}$ $d_{1}$thành $d_{2}$ $d_{2}$?

A. Vô số. B. $4$. C. $1$. D. $0$.

Câu 5. Phép tịnh tiến theo vectơ $\overrightarrow{v}$ $\overrightarrow{v}$ biến điểm $M$ thành điểm $M'$, khẳng định nào sau đây đúng?

A. $\overrightarrow{MM$ $\overrightarrow{MM'} = k\overrightarrow{v}$, $\left( k\mathbb{\in R} \right)$ $\left( k\mathbb{\in R} \right)$. B. $\overrightarrow{MM$ $\overrightarrow{MM'} = - \overrightarrow{v}$. C. $\overrightarrow{MM$ $\overrightarrow{MM'} = \overrightarrow{v}$. D. $\overrightarrow{M$ $\overrightarrow{M'M} = \overrightarrow{v}$.

Câu 6. Có bao nhiêu phép tịnh tiến biến một đường thẳng thành chính nó

A. 1. B. 2. C. Không có. D. Vô số.

Câu 7. Một phép tịnh tiến biến điểm $A$ thành điểm $B$ và điểm $C$ thành điểm $D$. Khẳng định nào sau đây là sai?

A. $ABCD$ là hình bình hành.

B. Trung điểm của hai đoạn thẳng $AD$ và $BC$ trùng nhau.

C. $\overrightarrow{AB} = \overrightarrow{CD}$ $\overrightarrow{AB} = \overrightarrow{CD}$.

D. $\overrightarrow{AC} = \overrightarrow{BD}$ $\overrightarrow{AC} = \overrightarrow{BD}$.

Cau 8. Cho đường thẳng $a$ cắt 2 đường thẳng song song $b$ và $b'$. Có bao nhiêu phép tịnh tiến biến $a$ thành chính nó và biến $b$ thành $b'$?

A. $1$. B. $0$. C. $2$. D. Vô số.

Câu 9. Trong mặt phẳng tọa độ $Oxy$, cho $\overrightarrow{v} = (2; - 1)$ $\overrightarrow{v} = (2; - 1)$. Tìm ảnh A' của $A( - 1;2)$ qua phép tịnh tiến theo vectơ $\overrightarrow{v}$ $\overrightarrow{v}$.

A. $A'( - 3;3)$. B. $A'(1;1)$. C. $A'\left( \frac{1}{2};\frac{1}{2} \right)$. D. $A'(3; - 3)$.

Câu 10. Trong mặt phẳng với hệ tọa độ $Oxy$, cho vectơ $\overrightarrow{v} =$ $\overrightarrow{v} =$ và điểm $M( - 3;\ \ 2).$ $M( - 3;\ \ 2).$ Tìm tọa độ ảnh $M'$ của điểm $M$ qua phép tịnh tiến theo vectơ $\overrightarrow{v}.$ $\overrightarrow{v}.$

A. $M'( - 1;1)$. B. $M'(1; - 1)$. C. $M'(5;3)$. D. $M'(1;1)$

Câu 11. Trong hệ tọa độ Oxy cho đường thẳng $d:\ x - 2y + 3 = 0$ $d:\ x - 2y + 3 = 0$. Phép tịnh tiến theo véc tơ $\overrightarrow{v} = (2;2)$ $\overrightarrow{v} = (2;2)$ biến đường thẳng d thành đường thẳng d’ có phương trình là

A. $2x - y + 5 = 0$ B. $x - 2y + 5 = 0$

C. $x + 2y + 5 = 0$ D. $x - 2y + 4 = 0$

Câu 12. Trong mặt phẳng tọa độ $Oxy$ cho $\overrightarrow{u} = (1; - 2)$ $\overrightarrow{u} = (1; - 2)$ và điểm $M(2; - 3)$. Ảnh của điểm $M$qua phép tịnh tiến theo vectơ $\overrightarrow{u}$ $\overrightarrow{u}$ là điểm có tọa độ nào trong các điểm sau?

A. $M( - 2;3)$. B. $M(1; - 3)$. C. $M(3; - 5)$. D. $M(1; - 1)$.

Câu 13. Trong mặt phẳng tọa độ $Oxy$ cho đường thẳng $\Delta$ $\Delta$ có phương trình $4x - y + 3 = 0$. Ảnh của đường thẳng $\Delta$ $\Delta$ qua phép tịnh tiến $T$ theo vectơ $\overrightarrow{v} = (2; - 1)$ $\overrightarrow{v} = (2; - 1)$ có phương trình là

A. $4x - y - 6 = 0$. B. $4x - y + 10 = 0$.

C. $4x - y + 5 = 0$. D. $x - 4y - 6 = 0$.

Câu 14. Trong mặt phẳng tọa độ $Oxy$ nếu phép tịnh tiến biến điểm $M(4;\ 2)$ $M(4;\ 2)$ thành điểm $M'(4;\ 5)$ thì nó biến điểm $A(2;\ 5)$ $A(2;\ 5)$ thành

A. điểm $A'(2;\ 8)$. B. điểm $A'(1;\ 6)$. C. điểm $A'(5;\ 2)$. D. điểm $A'(2;\ 5)$.

Câu 15. Trong hệ tọa độ $Oxy$ phép tịnh tiến theo vectơ $\overrightarrow{v\ }( - 1;2)$ $\overrightarrow{v\ }( - 1;2)$ biến điểm $A(2; - 3)$ thành điểm $B$ có tọa độ là.

A. $B( - 1; - 1)$. B. $B( - 1;1)$. C. $B(1; - 1)$. D. $B(1;1).$

Câu 16. Cho $M( - 2;\ 3)$ $M( - 2;\ 3)$. Hỏi điểm nào trong các điểm sau là ảnh của $M$ qua phép tịnh tiến theo $\overrightarrow{v}(1;\ - 2)$ $\overrightarrow{v}(1;\ - 2)$

A. $(1;\ 1).$ $(1;\ 1).$ B. $( - 3;\ 5).$ $( - 3;\ 5).$ C. $(3;\ - 5)$ $(3;\ - 5)$. D. $( - 1;\ 1).$ $( - 1;\ 1).$

Câu 17. Cho $\overrightarrow{v}(3; - 2)$ $\overrightarrow{v}(3; - 2)$ và đường tròn $(C):x^{2} + y^{2} - 4x + 4y - 1 = 0$ $(C):x^{2} + y^{2} - 4x + 4y - 1 = 0$. Ảnh của $(C)$ qua $T_{\overrightarrow{v}}$ $T_{\overrightarrow{v}}$ là $(C')$:.

A. $x^{2} + y^{2} + 8x + 2y - 4 = 0$ $x^{2} + y^{2} + 8x + 2y - 4 = 0$ B. $(x + 5)^{2} + (y - 4)^{2} = 9$ $(x + 5)^{2} + (y - 4)^{2} = 9$.

C. $(x + 1)^{2} + y^{2} = 9$ $(x + 1)^{2} + y^{2} = 9$. D. $(x - 5)^{2} + (y + 4)^{2} = 9$ $(x - 5)^{2} + (y + 4)^{2} = 9$.

Câu 18. Trong mặt phẳng với hệ tọa độ $Oxy$, cho vectơ $\overrightarrow{v} = (2;1)$ $\overrightarrow{v} = (2;1)$ và điểm $A(4;5)$. Hỏi $A$ là ảnh của điểm nào trong các điểm sau đây qua phép tịnh tiến theo $\overrightarrow{v}$ $\overrightarrow{v}$?

A. $I(2;4).$ B. $B(6;6).$ C. $D(1; - 1).$ D. $C( - 2; - 4).$

Câu 19. Cho điểm $M(1;\ 2)$ $M(1;\ 2)$ và $\overrightarrow{v} = (2;\ 1)$ $\overrightarrow{v} = (2;\ 1)$. Tọa độ điểm $M'$ là ảnh của $M$ qua phép tịnh tiến theo $\overrightarrow{v}$ $\overrightarrow{v}$ là

A. $M'(1;\ - 1)$. B. $M'( - 3;\ - 3)$. C. $M'( - 1;\ 1)$. D. $M'(3;\ 3)$.

Câu 20. Trong mặt phẳng tọa độ $Oxy$, tìm ảnh của đường thẳng $d:x + 2y - 3 = 0$ qua phép tịnh tiến theo $\overrightarrow{v} = (1; - 1)$ $\overrightarrow{v} = (1; - 1)$.

A. $d':x + 2y - 4 = 0$. B. $d':x - 2y - 4 = 0$. C. $d':x + 2y - 2 = 0$. D. $d': - x + 2y + 2 = 0$.

(Còn tiếp)

B. BẢNG ĐÁP ÁN TỔNG QUAN

C. HƯỚNG DẪN GIẢI CHI TIẾT

Câu 1: Theo tính chất của phép tịnh tiến: Phép tịnh tiến biến đường thẳng thành đường thẳng song song hoặc trùng với nó.

Câu 2:

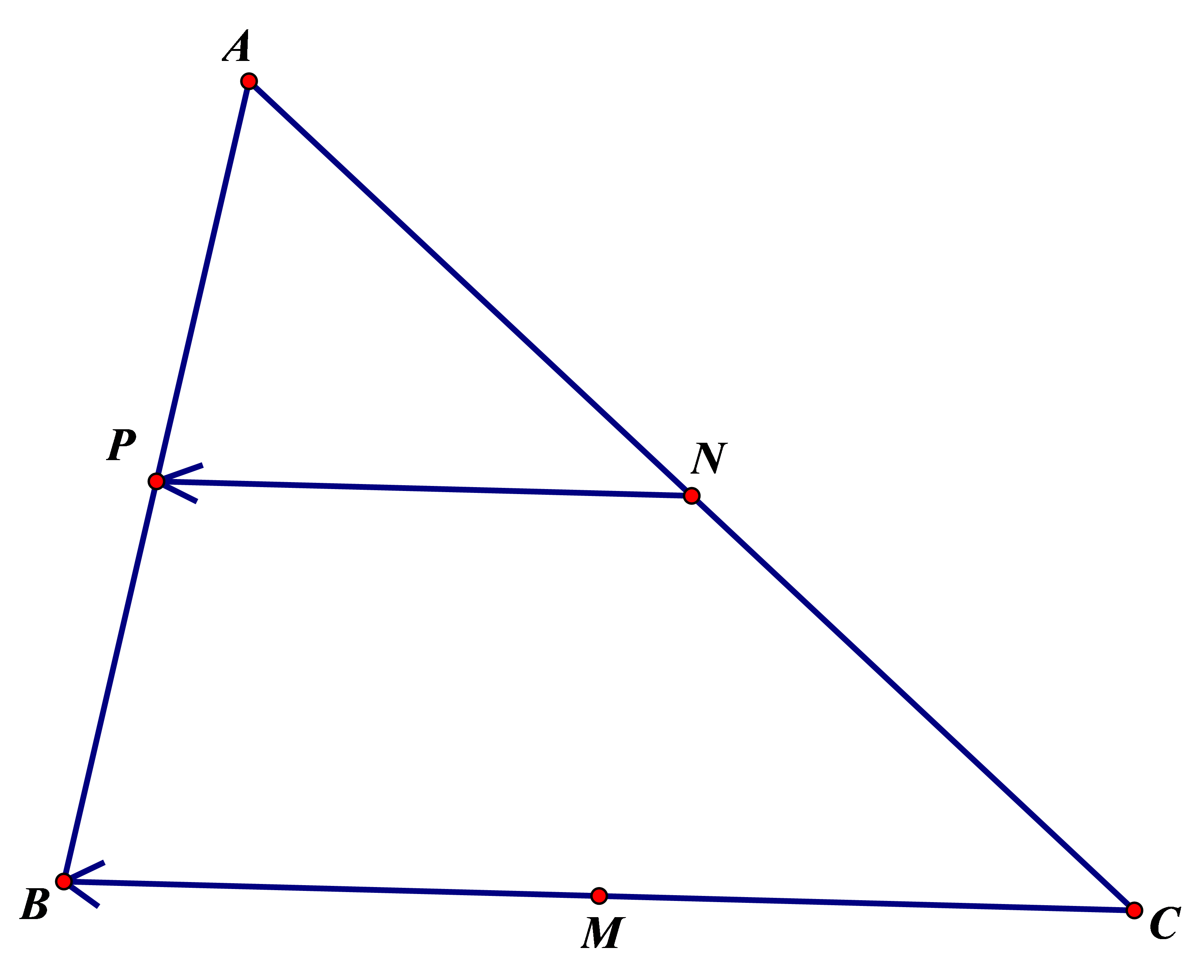
Vì $T_{\overrightarrow{u}}(N) = P$ $T_{\overrightarrow{u}}(N) = P$ nên $\overrightarrow{u} = \overrightarrow{NP} = - \frac{1}{2}\overrightarrow{BC}$ $\overrightarrow{u} = \overrightarrow{NP} = - \frac{1}{2}\overrightarrow{BC}$.

Câu 3: Do $T_{\overrightarrow{u}}(A) = A$ $T_{\overrightarrow{u}}(A) = A'\ \Leftrightarrow \ \overrightarrow{AA'} = \overrightarrow{u}\ \Rightarrow \ \overrightarrow{u} = (6;\ - 3)\ .$

Câu 4: Phép tịnh tiến biến đường thẳng thành đường thẳng song song hoặc trùng với nó mà $d_{1}$ $d_{1}$ không song song hoặc trùng với $d_{2}$ $d_{2}$nên không có phép tịnh tiến nào biến $d_{1}$ $d_{1}$thành $d_{2}$ $d_{2}$.

Câu 5: Theo định nghĩa phép tịnh tiến. $T_{\overrightarrow{v}}:M \mapsto M$ $T_{\overrightarrow{v}}:M \mapsto M' \Leftrightarrow \overrightarrow{MM'} = \overrightarrow{v}$.

Câu 6: Có vô số phép tịnh tiến biến một đường thẳng thành chính nó. Đó là các phép tịnh tiến có véc tơ tịnh tiến là véc tơ không hoặc véc tơ tịnh tiến là véc tơ chỉ phương của đường thẳng đó.

Câu 7: Phép tịnh tiến theo vectơ $\overrightarrow{v}$ $\overrightarrow{v}$ biến điểm $A$ thành điểm $B \Leftrightarrow \overrightarrow{AB} = \overrightarrow{v}$ $B \Leftrightarrow \overrightarrow{AB} = \overrightarrow{v}$.

Phép tịnh tiến theo vectơ $\overrightarrow{v}$ $\overrightarrow{v}$ biến điểm $C$ thành điểm $D \Leftrightarrow \overrightarrow{CD} = \overrightarrow{v}$ $D \Leftrightarrow \overrightarrow{CD} = \overrightarrow{v}$.

$\Rightarrow \overrightarrow{AB} = \overrightarrow{CD}$ $\Rightarrow \overrightarrow{AB} = \overrightarrow{CD}$ nên C đúng.

$\overrightarrow{AB} = \overrightarrow{CD} \Rightarrow$ $\overrightarrow{AB} = \overrightarrow{CD} \Rightarrow$ tứ giác $ABDC$ là hình bình hành có hai đường chéo $AD$ và $BC$ cắt nhau tại trung điểm mỗi đường nên B đúng.

$\overrightarrow{AB} = \overrightarrow{CD} \Leftrightarrow \overrightarrow{AC} + \overrightarrow{CB} = \overrightarrow{CB} + \overrightarrow{BD}$ $\overrightarrow{AB} = \overrightarrow{CD} \Leftrightarrow \overrightarrow{AC} + \overrightarrow{CB} = \overrightarrow{CB} + \overrightarrow{BD}$

$\Leftrightarrow \overrightarrow{AC} = \overrightarrow{BD}$ $\Leftrightarrow \overrightarrow{AC} = \overrightarrow{BD}$ nên D đúng.

Vậy A sai.

Tài liệu quá dài để hiển thị hết — hãy nhấn Tải về để xem trọn bộ!

-----------------------------------

Qua bộ bài tập Phép tịnh tiến Toán 11 có đáp án, hy vọng bạn đã hệ thống lại kiến thức và làm chủ toàn bộ dạng bài quan trọng nhất của chuyên đề này. Việc luyện tập thường xuyên sẽ giúp bạn tăng tốc độ làm bài, tránh sai sót và đạt điểm cao trong các bài kiểm tra, đánh giá học kỳ. Hãy lưu lại bài viết để thuận tiện ôn luyện và tiếp tục theo dõi website để nhận thêm nhiều tài liệu Toán 11 chuẩn – mới nhất – miễn phí.

Chúc bạn học tốt và đạt kết quả thật cao!

Xem thử Tải về

Chọn file muốn tải về: