Phương pháp chọn tập hợp đối tượng trước, sắp xếp sau
Phương pháp đếm trong tổ hợp - Có đáp án
Trong các dạng bài toán Tổ hợp – Chỉnh hợp – Hoán vị của chương trình Toán 11, phương pháp chọn tập hợp đối tượng trước, sắp xếp sau là một kỹ thuật giải cực kỳ quan trọng, giúp học sinh xử lý nhanh các bài toán đếm gắn với việc lựa chọn rồi sắp thứ tự. Bài viết này sẽ hướng dẫn bạn hiểu rõ bản chất của phương pháp, nắm được quy trình áp dụng, kèm ví dụ minh họa và bài tập trắc nghiệm có đáp án chi tiết. Đây là tài liệu hữu ích giúp bạn học vững phần tổ hợp và đạt điểm cao trong các bài kiểm tra và kỳ thi học kỳ.
- Dùng cho những bài toán có sự sắp xếp, cạnh nhau, có mặt….
- Trong những dạng toán này có những điều kiện mà ta phải chọn tập hợp đối tượng thoả mãn một vài điều kiện trước rồi mới sắp xếp để đạt được kết quả sau.
Ví dụ 1: Có bao nhiêu số tự nhiên có 4 chữ số đôi một khác nhau và khác 0 mà trong mỗi số luôn có mặt hai chữ số chẵn và hai chữ số lẻ?
Phân tích: Điều kiện của bài toán là: “4 chữ số” “khác nhau” “khác 0” “có mặt hai chữ số chẵn và hai chữ số lẻ”. Điều kiện: “4 chữ số” “khác nhau” không có gì đáng chú ý. Điều kiện “khác 0” chỉ đơn giản giúp ta không phải nghĩ đến trường hợp rắc rối khi số 0 đứng ở vị trí đầu. Điều kịên chủ chôt trong bài toán là: “có mặt hai chữ số chẵn và hai chữ số lẻ”. Do vậy ta cần chọn trước 2 chữ số chẵn và 2 chữ số lẻ rồi xếp vị trí cho các chữ số đó.
Lập sơ đồ bài toán như sau:

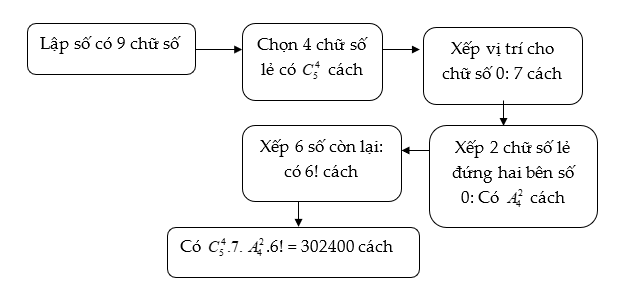
Ví dụ 2: Có bao nhiêu số tự nhiên có 9 chữ số khác nhau mà trong mỗi số có đúng 4 chữ số lẻ và chữ số 0 đứng giữa hai chữ số lẻ (các chữ số liền trước và liền sau của chữ số 0 đều là số lẻ)?
Phân tích: Điều kiện chủ chốt trong bài toán là: “có đúng 4 chữ số lẻ và chữ số 0 đứng giữa 2 chữ số lẻ”. Do vậy ta cần chọn trước 4 chữ số lẻ, rồi ưu tiên xếp vị trí cho chữ số 0, chọn 2 số lẻ xếp trước và sau chữ số 0, rồi ta xếp vị trí cho 6 số còn lại.
Sơ đồ của bài toán như sau:
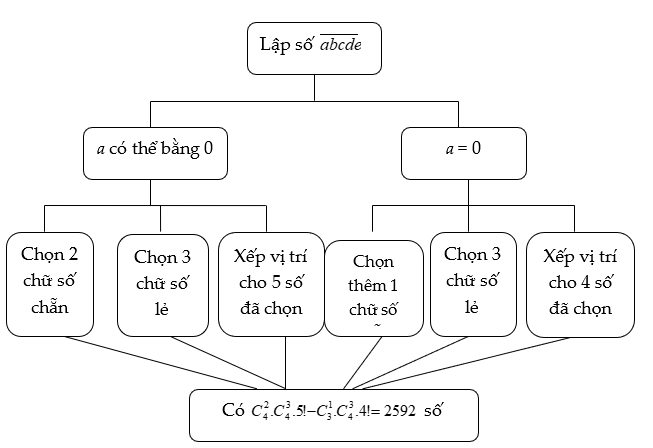
Ví dụ 3: Từ các chữ số 0,1,2,3,4,5,6,7 có thể lập được bao nhiêu số tự nhiên gồm 5 chữ số đôi một khác nhau và trong mỗi số đó có đúng 2 chữ số chẵn và 3 chữ số lẻ?
Phân tích: Điều kiện chủ chốt trong bài toán là: “có đúng 2 chữ số chẵn và 3 chữ số lẻ”, ở bài toán này ta dùng phương pháp lấy trước rồi xếp sau. Mặt khác các số đề bài cho có cả số 0 nên ta sử dụng kết hợp thêm phương pháp phần bù:
Sơ đồ của bài toán như sau:
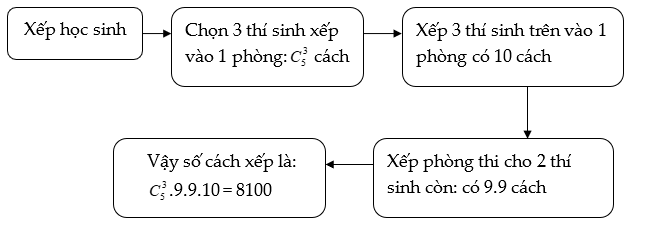
Ví dụ 4: Trong kỳ thi THPT quốc gia, tại hội đồng thi X, trường THPT A có 5 thí sinh dự thi. Hỏi có bao nhiêu cách xếp 3 thí sinh của trường THPT A được xếp vào một phòng thi, biết rằng hội đồng thi X có 10 phòng thi, mỗi phòng thi có nhiều hơn 5 thí sinh và việc xếp các thí sinh vào các phòng thi là hoàn toàn ngẫu nhiên?
Phân tích: Điều kiện chủ chốt của bài toán này là “3 thí sinh của trường A được xếp vào 1 phòng thi”. Để giải quyết bài toán này thì chúng ta chọn 3 thí sinh sau đó xếp 3 thí sinh này vào 1 phòng thi. Tiếp theo chúng ta sẽ xếp 2 thí sinh còn lại vào các phòng thi khác với phòng thi xếp 3 thí sinh trước.
Sơ đồ của bài toán như sau:
-------------------------
Phương pháp “chọn tập hợp đối tượng trước, sắp xếp sau” là một chìa khóa giúp đơn giản hóa nhiều dạng bài toán đếm trong chương trình Toán 11. Khi nắm vững kỹ thuật này, bạn sẽ dễ dàng nhận dạng cấu trúc bài toán, lập luận chính xác và rút ngắn thời gian làm bài. Hãy tiếp tục luyện tập với nhiều dạng bài khác trong chủ đề Tổ hợp – Chỉnh hợp – Hoán vị để củng cố tư duy tổ hợp và tăng tốc độ phản xạ khi thi. Chúc bạn học tốt và đạt kết quả cao!










