Phương pháp đếm trực tiếp giải bài toán tổ hợp
Cách đếm trực tiếp trong tổ hợp
Phương pháp đếm trực tiếp là nền tảng quan trọng trong chương trình Tổ hợp – Chỉnh hợp – Hoán vị Toán 11, giúp học sinh tư duy logic và giải quyết nhanh các bài toán đếm số trường hợp. Bài viết này tổng hợp các bài tập minh họa cùng phương pháp giải chi tiết, giúp bạn nắm vững cách đếm trực tiếp, tránh sai sót và làm chủ các dạng toán tổ hợp thường gặp trong đề kiểm tra và đề thi.
A. Cách đếm trực tiếp
Đây là hướng tư duy trong phần lớn các bài toán đếm, đặc điểm của phương pháp này là chúng ta chia nhỏ công việc cần thực hiện thành các phần nhỏ hơn để đếm.
B. Bài tập minh họa phương pháp đếm trực tiếp
Ví dụ 1: Cho các số 0,1,2,3,4,5,6. Hỏi từ các chữ số trên có thể lập được bao nhiêu số tự nhiên chẵn gồm 4 chữ số khác nhau.
Phân tích: Chúng ta thấy điều kiện chủ chốt của bài toán là “số tự nhiên chẵn”. Như vậy thì chữ số hàng đơn vị phải là số chẵn. Dẫn đến phải chọn d ngay từ bước đầu tiên.
Lập sơ đồ bài toán như sau:
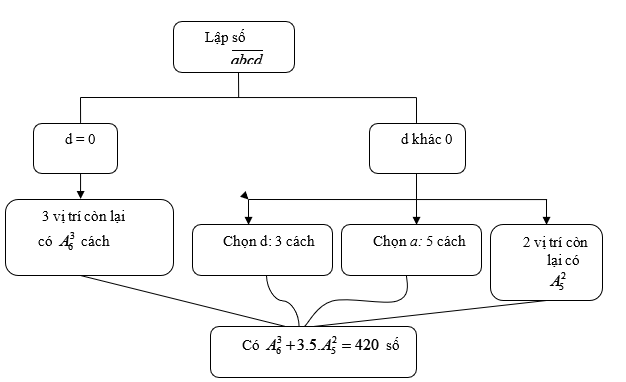
Hướng dẫn giải
Gọi số cần lập là 
\(\overline{abcd}\)
TH1: d = 0 số cách chọn 3 chữ số còn lại là \(A_{6}^{3}\)
TH2: d\(\neq\) 0 khi đó có 3 cách chọn d. 5 cách chọn a và số cách chọn 2 chữ số còn lại là \(A_{5}^{2}\)
Vậy số các số cần tìm là: \(A_{6}^{3} +
3.5.A_{5}^{2} = 420\) số.
Qua ví dụ trên ta thấy sau khi lập sơ đồ thiết kế, tính toán đưa ra được đáp số chính xác thì việc trình bày lời giải là không khó. Các em học sinh cần lựa chọn từ ngữ diễn đạt để trình bày lời giải. Vì vậy ở các ví dụ sau tôi chỉ đưa ra cách phân tích, thiết kế, lập sơ đồ của bài toán, từ đó các em sẽ diễn đạt trình bày lời giải của bài toán
Ví dụ 2: Cho các chữ số 0,1,2,3,4,5,6. Từ các chữ số đó có thể lập được bao nhiêu số tự nhiên có 5 chữ số đôi một khác nhau và phải có mặt chữ số 1 và 2.
Phân tích: Điều kiện chủ chốt của bài là “phải có mặt chữ số 1 và 2”. Do đó trước hết phải chọn vị trí cho chữ số 1 và 2. Tuy nhiên do chữ số hàng chục nghìn khác 0 nên việc 1 hoặc 2 rơi vào vị trí hàng chục nghìn sẽ ảnh hưởng tới bước xếp các chữ số 0,3,4,5,6 vào các vị trí còn lại.
Lập sơ đồ bài toán như sau:
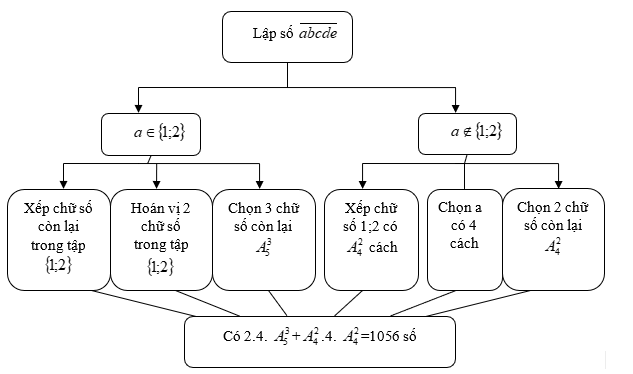
Ví dụ 3: Có 5 nhà toán học nam, 3 nhà toán học nữ, 4 nhà vật lý nam. Lập một đoàn công tác gồm 3 người cần có cả nam và cả nữ, có nhà toán học lẫn nhà vật lý học. Hỏi có bao nhiêu cách lập đoàn công tác?
Phân tích: Trước hết đoàn công tác cần có cả nam và nữ, sau lại có cả nhà toán học lẫn nhà vật lý học. Do đó số lượng nhà vật lý trong nhóm sẽ ảnh hưởng đến số cách chọn người nữ. Bởi vậy ta chia trường hợp theo số lượng nhà khoa học các ngành: 2 lý – 1 toán và 2 toán - 1 lý.
Lập sơ đồ bài toán như sau:
---------------------------------------------------------
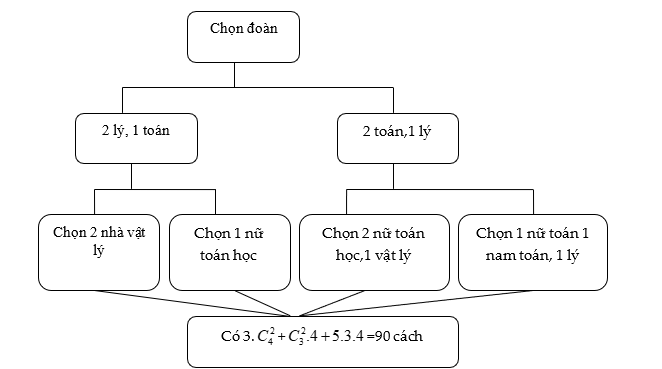
Thông qua việc luyện tập với phương pháp đếm trực tiếp, bạn sẽ hiểu rõ bản chất của các bài toán tổ hợp và áp dụng hiệu quả vào những dạng bài phức tạp hơn như chỉnh hợp, hoán vị hay bài toán xếp chỗ. Hãy tiếp tục thực hành để nâng cao tốc độ tư duy và củng cố nền tảng vững chắc cho chương trình Toán 11 cũng như các kỳ thi quan trọng.
