Phương pháp đếm phần bù giải bài toán tổ hợp
Đếm phần bù trong tổ hợp - Có đáp án
Phương pháp đếm phần bù là một kỹ thuật thông minh và hiệu quả trong chủ đề Tổ hợp – Chỉnh hợp – Hoán vị Toán 11, giúp học sinh giải nhanh các bài toán đếm khi việc liệt kê trực tiếp trở nên phức tạp. Bài viết này cung cấp hệ thống bài tập minh họa kèm lời giải chi tiết, giúp bạn hiểu rõ cách sử dụng phần bù để tính số trường hợp nhanh, chính xác và tránh sai sót.
Cơ sở của phương pháp đếm là thay vì đếm số phần tử của tập A trực tiếp thì ta sẽ đếm số phần tử của tập hợp 
\(\overline{A}\). Trong phương pháp này tôi sử dụng kí hiệu này 
để biểu thị phương pháp đếm phần bù.
Ví dụ 1: Cho các số 0, 1, 2, 3, 4, 5, 6. Hỏi từ các chữ số trên có thể lập được bao nhiêu số tự nhiên chẵn gồm 4 chữ số khác nhau?
Lập sơ đồ bài toán như sau:
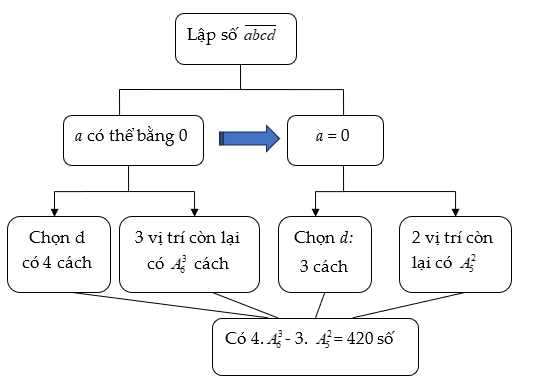
Phân tích: Đây là ví dụ 1 của phần phương pháp đếm trực tiếp. Để sử dụng phương pháp đếm phần bù, trước hết phân tích như sau. Các bước thiết kế công việc hoàn toàn tương tự như cách giải trên. Có thể thấy rõ điều khác căn bản của hai phương pháp đếm trên là thay vì tính số cách lập bằng phương pháp nhân thì ta tính bằng phép trừ.
Ví dụ 2: Từ các chữ số 0, 1, 2, 3, 4, 5, 6, 7, 8 có thể lập được bao nhiêu số tự nhiên gồm 5 chữ số đôi một khác nhau và không bắt đầu bởi 123?
Lập sơ đồ bài toán như sau:
Ví dụ 3: Từ một tập thể 14 người gồm 6 nam và 8 nữ trong đó có A và B, người ta muốn chọn một tổ công tác gồm 6 người. Tìm số cách chọn trong mỗi trường hợp sau:
a, Trong tổ phải có cả nam và nữ.
b, Trong tổ có 1 tổ trưởng, 5 tổ viên hơn nữa A và B không đồng thời có mặt trong tổ.
Phân tích:
Với ý a, để đếm trực tiếp số cách chọn tổ có cả nam và nữ thì ta phải xây dựng được một sơ đồ công việc để chọn một tổ có cả nam và nữ. chẳng hạn như: Bước1: chọn một bạn nam, bước 2: chọn một bạn nữ, bước 3: chọn 4 bạn còn lại. Cách chọn trên đảm bảo điều kiện có “cả nam và nữ” tuy nhiên lại không thể dùng để đếm được vì hai cách chọn khác nhau lại cho cùng một đội. Vì vậy để giải quyết bài toán này ta dùng phương pháp đếm phần bù của trường hợp cần đếm là các trường hợp “6 người toàn nam” và “6 người toàn nữ”.
Với ý b, ta vẫn có thể sử dụng phương pháp đếm trực tiếp. Tuy nhiên cách sử dụng phần bù giúp tiết kiệm được tính toán.
Lập sơ đồ bài toán như sau:
Ý a)
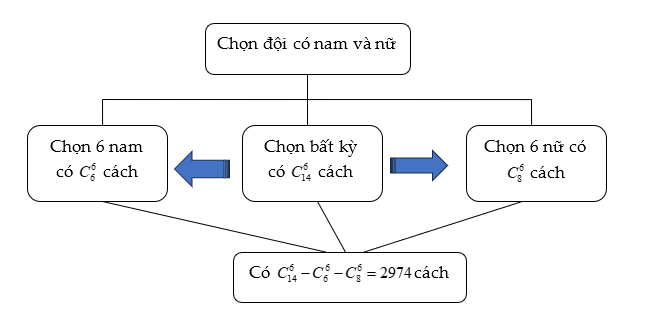
Ý b)
----------------------------------
Việc thành thạo đếm phần bù không chỉ giúp bạn giải quyết nhiều dạng bài tổ hợp khó mà còn nâng cao tư duy logic trong các bài toán đếm và xếp chỗ. Hãy tiếp tục luyện tập với nhiều tình huống đa dạng để củng cố kiến thức và tự tin chinh phục mọi đề thi Toán 11 liên quan đến tổ hợp, chỉnh hợp và hoán vị.
