Bài tập Đối xứng trục: 20+ Câu trắc nghiệm cơ bản nhất

Phép đối xứng trục là kiến thức trọng tâm trong chương trình Hình học Oxy của Chuyên đề Toán 11, thường xuất hiện trong các bài kiểm tra và đề thi. Để giúp học sinh rèn luyện kỹ năng nhận dạng và áp dụng công thức nhanh chóng, bài viết này tổng hợp 20+ câu trắc nghiệm đối xứng trục cơ bản nhất, bám sát nội dung sách giáo khoa và phù hợp cho mọi đối tượng học sinh. Mỗi câu hỏi đều được biên soạn ngắn gọn, rõ ràng và đi kèm đáp án chính xác, giúp bạn ôn tập hiệu quả và nâng cao tư duy khi làm bài.

A. ĐỀ BÀI TRẮC NGHIỆM PHÉP ĐỐI XỨNG TRỤC

Câu 1. Hình vuông có mấy trục đối xứng?

A. 1             B. 2         C. 4           D. vô số

Câu 2: Trong mặt phẳng \(Oxy\) cho điểm \(M(2;3)\). Hỏi trong bốn điểm sau điểm nào là ảnh của \(M\)qua phép đối xứng trục \(Ox\)?

A. \((3;2)\).          B. \((2; - 3)\).           C. \((3; - 2)\).               D. \(( - 2;3)\).

Câu 3: Trong mặt phẳng \(Oxy\) cho điểm \(M(2;3)\) . Hỏi \(M\) là ảnh của điểm nào trong các điểm sau qua phép đối xứng trục \(Oy\) ?

A. \((3;2)\).              B. \((2; - 3)\).            C. \((3; - 2)\).          D. \(( - 2;3)\).

Câu 4: Trong mặt phẳng \(Oxy\) cho điểm \(M(2;3)\) . Hỏi trong bốn điểm sau điểm nào là ảnh của \(M\) qua phép đối xứng qua đường thẳng \(\Delta:x - y = 0\) ?

A. \((3;2)\) .              B. \((2; - 3)\) .             C. \((3; - 2)\) .            D. \(( - 2;3)\) .

Câu 5: Hình gồm hai đường tròn có tâm và bán kính khác nhau có bao nhiêu trục đối xứng?

A. Không có.         B. Một.         C. Hai.           D. Vô số.

Câu 6: Hình gồm hai đường thẳng \(d\) và \(d'\) vuông góc với nhau đó có mấy trục đối xứng?

A. \(0\) .                B. \(2\) .             C. \(4\) .           D. Vô số.

Câu 7: Trong các mệnh đề sau mệnh đề nào đúng?

A. Đường tròn là hình có vô số trục đối xứng.

B. Một hình có vô số trục đối xứng thì hình đó phải là hình tròn.

C. Một hình có vô số trục đối xứng thì hình đó phải là hình gồm những đường tròn đồng tâm.

D. Một hình có vô số trục đối xứng thì hình đó phải là hình gồm hai đường thẳng vuông góc.

Câu 8: Xem các chữ cái in hoa \(A,B,C,D,X,Y\) như những hình. Khẳng định nào sau đậy đúng?

A. Hình có một trục đối xứng: \(A,Y\)và các hình khác không có trục đối xứng.

B. Hình có một trục đối xứng: \(A,B,C,D,Y\). Hình có hai trục đối xứng: \(X\).

C. Hình có một trục đối xứng: \(A,B\) và hình có hai trục đối xứng: \(D,X\).

D. Hình có một trục đối xứng: \(C,D,Y\). Hình có hai trục đối xứng: \(X\). Các hình khác không có trục đối xứng.

Câu 9: Giả sử rằng qua phép đối xứng trục \(Đ_{a}\) (\(a\) là trục đối xứng), đường thẳng \(d\) biến thành đường thẳng \(d'\) . Hãy chọn câu sai trong các câu sau:

A. Khi \(d\) song song với \(a\) thì \(d\) song song với \(d'\).

B. \(d\) vuông góc với \(a\) khi và chỉ khi \(d\) trùng với \(d'\).

C. Khi \(d\) cắt \(a\) thì \(d\) cắt \(d'\). Khi đó giao điểm của \(d\) và \(d'\) nằm trên \(a\).

D. Khi \(d\) tạo với \(a\) một góc \(45^{0}\) thì \(d\) vuông góc với \(d'\).

Câu 10: Trong mặt phẳng \(Oxy\) , cho Parapol \((P)\) có phương trình \(x^{2} = 24y\) . Hỏi Parabol nào trong các parabol sau là ảnh của \((P)\) qua phép đối xứng trục \(Oy\) ?

A. \(x^{2} = 24y\).         B. \(x^{2} = - 24y\).         C. \(y^{2} = 24x\).      D. \(y^{2} = - 24x\).

Câu 11: Trong mặt phẳng \(Oxy\) , cho parabol \((P):y^{2} = x\). Hỏi parabol nào sau đây là ảnh của parabol \((P)\) qua phép đối xứng trục \(Oy\) ?

A. \(y^{2} = x\) .             B. \(y^{2} = - x\) .           C. \(x^{2} = - y\) .             D. \(x^{2} = y\) .

Câu 12: Trong mặt phẳng \(Oxy\) cho parabol \((P)\) có phương trình \(x^{2} = 4y\) . Hỏi parabol nào trong các parabol sau là ảnh của \((P)\) qua phép đối xứng trục \(Ox\) ?

A. \(x^{2} = 4y\) .           B. \(x^{2} = - 4y\) .         C. \(y^{2} = 4x\) .             D. \(y^{2} = - 4x\) .

Câu 13: Trong mặt phẳng \(Oxy\), qua phép đối xứng trục \(Oy\) . Điểm \(A(3;5)\) biến thành điểm nào trong các điểm sau?

A. \((3;5)\) .            B. \(( - 3;5)\) .         C. \((3; - 5)\) .              D. \(( - 3; - 5)\) .

Câu 14: Cho \(3\) đường tròn có bán kính bằng nhau và đôi một tiếp xúc ngoài với nhau tạo thành hình \((H)\) . Hỏi \((H)\) có mấy trục đối xứng?

A. \(0\).             B. \(1\) .              C. \(2\).                  D. \(3\).

(Còn tiếp)

B. ĐÁP ÁN TỔNG QUAN

C. HƯỚNG DẪN GIẢI CHI TIẾT

Câu 1. Chọn C

Câu 2:

Gọi \(M'(x';y')\) là ảnh của điểm \(M(x;y)\) qua phép đối xứng trục \(Ox\) ta có:

\(\left\{ \begin{matrix} x' = x \\ y' = - y \end{matrix} \right.\ \Rightarrow \left\{ \begin{matrix} x' = 2 \\ y' = - 3 \end{matrix} \right.\).

Vậy \(M'(2; - 3)\).

Chọn B.

Câu 3:

Gọi \(M'(x';y')\) là ảnh của điểm \(M(x;y)\) qua phép đối xứng trục \(Oy\) ta có:

\(\left\{ \begin{matrix} x' = - x \\ y' = y \end{matrix} \right.\ \Rightarrow \left\{ \begin{matrix} x' = - 2 \\ y' = 3 \end{matrix} \right.\).

Vậy \(M'( - 2;3)\).

Chọn D.

Câu 4:

Gọi \(M'(x';y')\) là ảnh của điểm \(M(x;y)\) qua phép đối xứng qua \(\Delta:x - y = 0\).

Gọi \(d\) là đường thẳng đi qua điểm \(M(2;3)\) và vuông góc \(\Delta:x - y = 0\) ta có:

\(d:x + y - 5 = 0\).

Gọi \(I = d \cap \Delta\) thì \(I\left( \frac{5}{2};\frac{5}{2} \right)\).

Khi đó \(I\) là trung điểm của \(MM'\) nên suy ra \(M'(3;2)\).

Chọn A.

Câu 5:

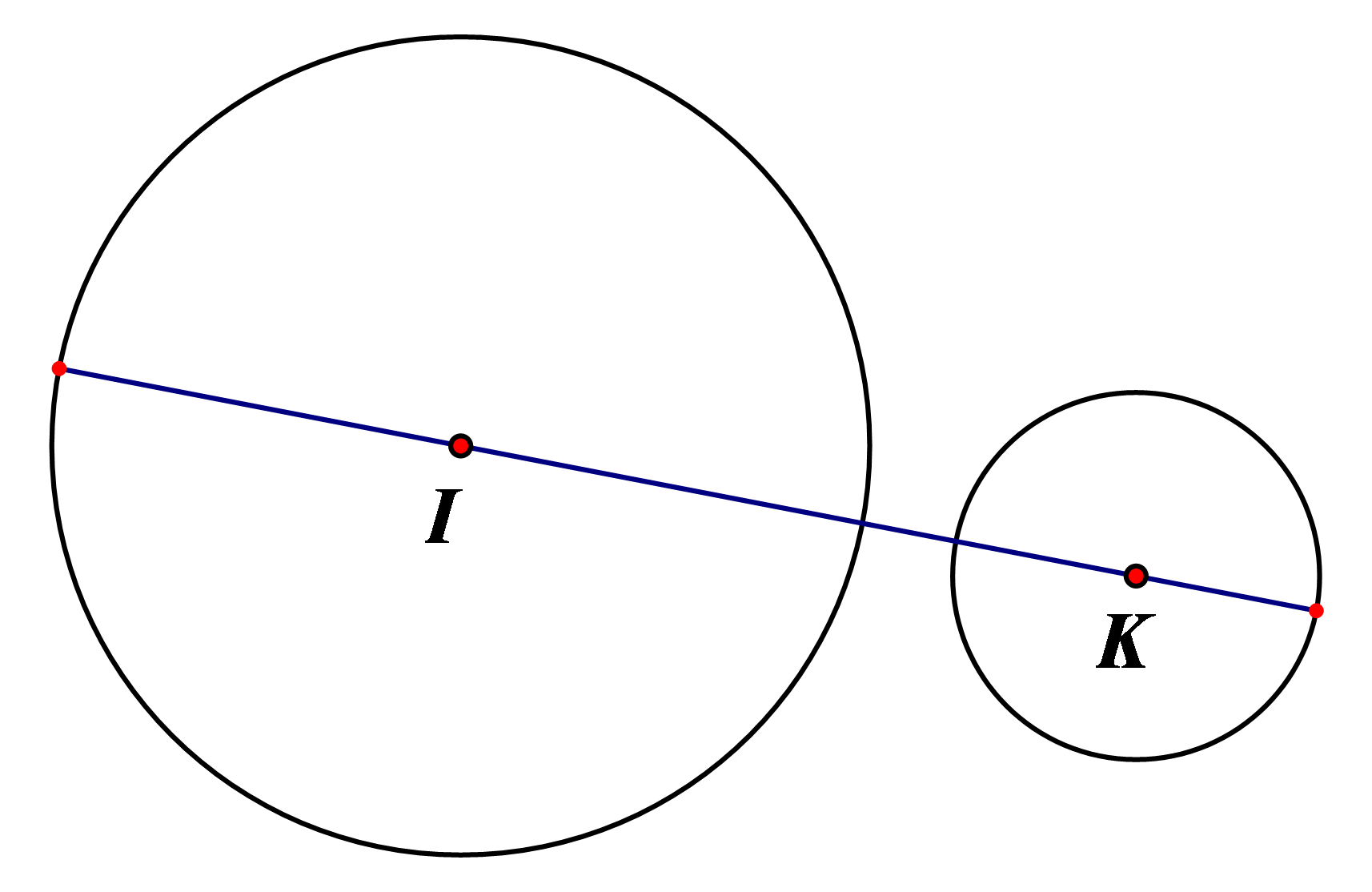
Chọn B.

Câu 6:

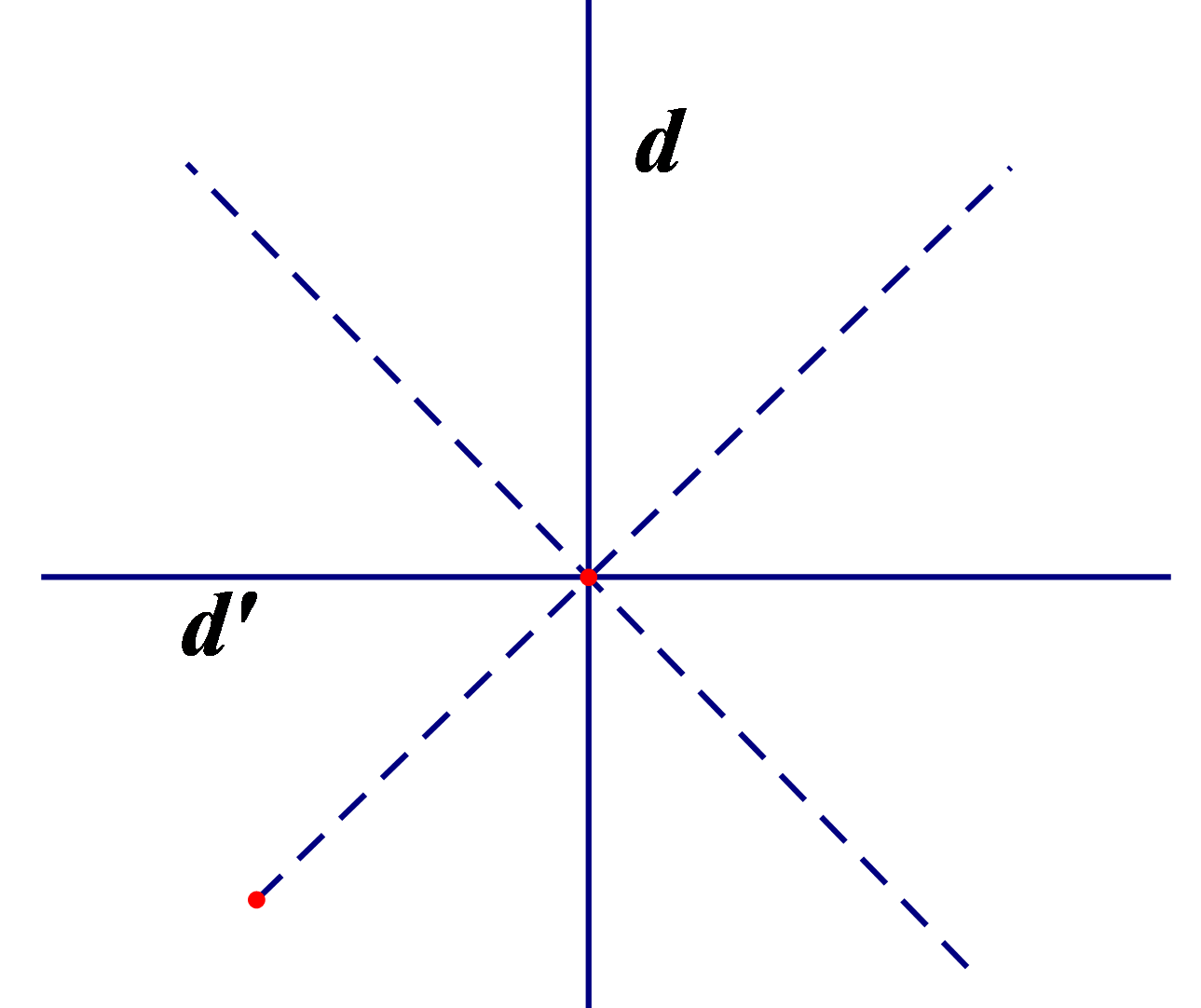
Ta có \(2\) trục đối xứng là \(2\) đường thẳng đó và \(2\) đường phân giác tạo bởi \(2\) đường thẳng đó.

Chọn C.

Câu 7:

Các đường kính của đường tròn là các trục đối xứng.

Chọn A.

Không thể hiển thị hết nội dung tại đây — bấm Tải về để lấy toàn bộ tài liệu.

-----------------------------------

Hy vọng bộ bài tập trắc nghiệm đối xứng trục cơ bản đã giúp bạn củng cố kiến thức nền tảng và thành thạo các dạng bài thường gặp trong chuyên đề. Hãy tiếp tục luyện tập thêm nhiều bài tập khác trong hệ thống Chuyên đề Toán 11 có đáp án để cải thiện tốc độ, tăng độ chính xác và tự tin hơn trong các bài kiểm tra. Chúc bạn học tốt và đạt kết quả cao!