Cách dựng thiết diện chứa yếu tố vuông góc
Bài tập dựng thiết diện chứa yếu tố vuông góc có đáp án
Trong các bài toán thiết diện hình học không gian Toán 11, dạng dựng thiết diện chứa yếu tố vuông góc thường gây khó khăn do yêu cầu xác định chính xác quan hệ vuông góc giữa các đường và mặt. Nếu không nắm rõ phương pháp dựng hình, học sinh rất dễ xác định sai thiết diện. Bài viết này sẽ hướng dẫn cách dựng thiết diện chứa yếu tố vuông góc theo trình tự rõ ràng, kèm bài tập có đáp án, giúp người học tiếp cận bài toán đúng bản chất và giải quyết hiệu quả.
A. Bài tập minh họa dựng thiết diện có yếu tố vuông góc
Bài tập 1. Cho tứ diện 
\(SABC\) có đáy là tam giác \(ABC\) đều cạnh \(a,\) \(SA\bot(ABC)\) và \(SA = a.\) Tìm thiết diện của tứ diện \(SABC\) với \((\alpha)\) và tính diện tích thiết diện trong các trường hợp sau:
a) \((\alpha)\) qua \(S\) và vuông góc với \(BC.\)
b) \((\alpha)\) qua \(A\) và vuông góc với trung tuyến \(SI\) của \(\Delta
SBC.\)
Hướng dẫn giải
Hình vẽ minh họa:
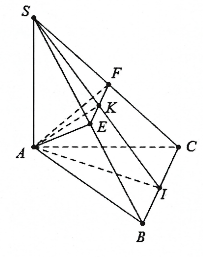
a) Gọi \(I\) là trung điểm của \(BC\) thì \(AI\bot
BC\)
Mặt khác \(SA\bot(ABC) \Rightarrow SA\bot
BC \Rightarrow BC\bot(SAI)\)
Thiết diện của khối chóp qua \(S\) và vuông góc với \(BC\) là tam giác \(SAI\) vuông tại \(A\) có \(SA = a;\
\ AI = \frac{a\sqrt{3}}{2}.\)
Do đó \(S_{SAI} = \frac{1}{2}SA.AI =
\frac{a^{2}\sqrt{3}}{4}.\)
b) Dựng \(AK\bot SI,\) lại có \(BC\bot(SAI) \Rightarrow BC\bot AK\)
Suy ra \(AK\bot(SBC) \Rightarrow AK\bot
SI.\)
Qua \(K\) dựng đường thẳng vuông góc với \(SI\) cắt \(SB,\ \ SC\) lần lượt tại \(E\) và \(F
\Rightarrow\) thiết diện là tam giác \(AEF.\)
Ta có: \(AK = \frac{SA.AI}{\sqrt{SA^{2} +
AI^{2}}} = \frac{a\sqrt{21}}{7}.\)
Tam giác \(SAI\) vuông tại \(A\) có đường cao \(AH\) nên:
\(SA^{2} = SK.SI\)
\(\Rightarrow \frac{SA^{2}}{SI^{2}} =
\frac{SK}{SI} = \frac{EF}{BC} = \frac{SA^{2}}{SA^{2} + AI^{2}} =
\frac{4}{7}\)
Do đó \(EF = \frac{4}{7}a \Rightarrow
S_{AEF} = \frac{1}{2}AK.EF = \frac{2a^{2}\sqrt{21}}{49}.\)
Bài tập 2. Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh \(a,\) các cạnh bên đều bằng \(\frac{a\sqrt{3}}{2}.\) Mặt phẳng \((\alpha)\) đi qua \(A,\) song song với \(BC\) và vuông góc với mặt phẳng \((SBC),\) xác định thiết diện của mặt phẳng \((\alpha)\) với hình chóp và tính diện tích thiết diện.
Hướng dẫn giải
Hình vẽ minh họa:
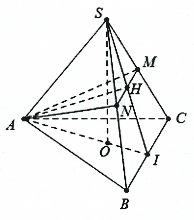
Gọi \(O\) là trọng tâm tam giác \(ABC\) thì \(SO\bot(ABC)\) (Do \(S.ABC\) là khối chóp đều).
Gọi \(I\) là trung điểm của \(BC\) thì \(AI\bot
BC\) mà \(BC\bot SO\) suy ra \(BC\bot(SAI).\)
Dựng \(AH\bot SI,\) lại có \(BC\bot(SAI) \Rightarrow BC\bot AH\)
Suy ra \(AH\bot(SBC).\) Qua \(K\) dựng đường thẳng song song với \(BC\) cắt \(SB,\ \
SC\) lần lượt tại \(N\) và \(M \Rightarrow\) Thiết diện là tam giác \(AMN.\)
Ta có: \(SA = AI = \frac{a\sqrt{3}}{2}
\Rightarrow H\) là trung điểm của \(SI.\)
Suy ra \(MN = \frac{1}{2}BC =
\frac{a}{2}.\)
Lại có: \(SI = \sqrt{SB^{2} - IB^{2}} =
\frac{a\sqrt{2}}{2} \Rightarrow HI = \frac{a\sqrt{2}}{4}\)
Khi đó \(AH = \sqrt{AI^{2} - HI^{2}} =
\frac{a\sqrt{10}}{4}\)
\(\Rightarrow S_{AMN} = \frac{1}{2}AH.MN =
\frac{a^{2}\sqrt{10}}{16}.\)
Bài tập 3. Cho hình lập phương \(ABCD \cdot
A'B'C'D'\) có cạnh bằng \(a\).
a) Tính độ dài đường chéo của hình lập phương.
b) Chứng minh rằng \((ACC'A')\bot(BDD'B')\).
c) Gọi \(O\) là tâm của hình vuông \(ABCD\). Chứng minh rằng \(\widehat{COC'}\) là một góc phẳng của góc nhị diện \(\lbrack
C,BD,C'\rbrack\). Tính (gần đúng) số đo của các góc nhị diện \(\lbrack C,BD,C\rbrack,\lbrack
A,BD,C'\rbrack\).
Hướng dẫn giải
Hình vẽ minh họa:
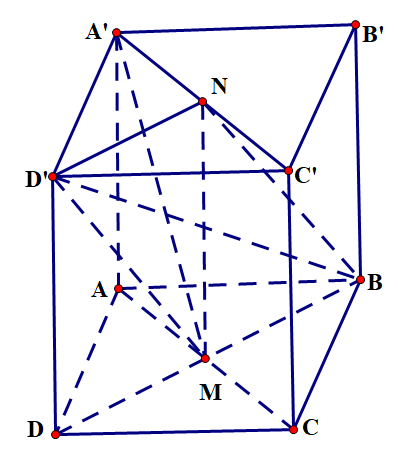
a) Độ dài đường chéo của hình lập phương có thể tính từ công thức cạnh đường chéo của hình lập phương như sau: \(d = \sqrt{a^{2} + a^{2} + a^{2}} =
\sqrt{3}a\)
b) Ta có \(AC^{2} + CA^{'2} =
AA^{'2}\) do tam giác vuông \(ACA'\) nên ta có \(AC = CA' = \frac{a}{\sqrt{2}}\)
Tương tự \(BD^{2} = DB^{'2} = BC^{2} =
CB^{'2} = AD^{2} = DA^{'2} = a^{2}\).
Gọi \(M,N\) lần lượt là trung điểm của các cạnh \(BD,A'C'\) thì \(MN//AC//A'C'\) và \(MN = \frac{1}{2}a^{2} +
\frac{1}{2}a^{2}a^{2}\)
Do \(AMD'\) và \(D'BN\) là hai tam giác vuông cân tại \(M,N\).
Suy ra \((ACC'A')\bot(BDD'B')\)
B. Bài tập tự rèn luyện dựng thiết diện có hướng dẫn chi tiết
Bài tập 1. Cho hình chóp \(S.ABCD\) có \(ABCD\) là hình thang vuông tại \(A\) và \(B\) với \(AB = BC
= a,\) \(AD = 2a,\) \(SA\bot(ABCD)\) và \(SA = 2a.\) Gọi M là một điểm trên cạnh \(AB,\) \((\alpha)\) là mặt phẳng qua \(M\) và vuông góc với \(AB.\) Đặt \(x =
AM(0 < x < a).\)
a) Tìm thiết diện của hình chóp với \((\alpha).\) Thiết diện là hình gì?
b) Tính diện tích thiết diện theo \(a\) và \(x.\)
Bài tập 2. Cho tứ diện \(SABC\) có đáy \(ABC\) là tam giác vuông cân đỉnh \(B,\) \(AB =
a,\) \(SA\bot(ABC)\) và \(SA = a\sqrt{3}.\) Điểm \(M\) là một điểm tuỳ ý trên cạnh \(AB,\) đặt \(AM =
x,(0 < x < a).\) Gọi \((\alpha)\) là mặt phẳng qua \(M\) và vuông góc với \(AB.\)
a) Tìm thiết diện của tứ diện \(SABC\) với \((\alpha).\)
b) Tính diện tích của thiết diện theo \(a\) và \(x.\) Tìm \(x\) để diện tích này có giá trị lớn nhất.
Bài tập 3. Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a,\) \(SA\bot(ABCD).\) Gọi \((\alpha)\) là mặt phẳng chứa \(AB\) và vuông góc với mặt phẳng \((SCD).\)
a) \((\alpha)\) cắt khối chóp \(S.ABCD\) theo thiết diện là hình gì?
b) Biết \(SA = a.\) Tính diện tích thiết diện tìm được ở câu \(a.\)
📚 Phần tiếp theo của tài liệu đã được tổng hợp trong file đính kèm, mời bạn tải về để đọc tiếp.
-----------------------------------------------
Khi nắm vững phương pháp dựng thiết diện có yếu tố vuông góc, học sinh sẽ xử lý các bài toán thiết diện trong không gian một cách tự tin và chính xác hơn. Hệ thống bài tập Toán 11 có đáp án giúp củng cố kỹ năng dựng hình, hạn chế sai sót và nâng cao khả năng vận dụng trong các dạng bài liên quan.
