Xác định và tính số đo góc phẳng nhị diện
Góc phẳng nhị diện Toán 11
Trong chương Hình học không gian Toán 11, nội dung góc phẳng nhị diện là kiến thức quan trọng nhưng thường gây khó khăn do học sinh chưa xác định đúng yếu tố tạo góc. Việc xác định và tính số đo góc phẳng nhị diện đòi hỏi hiểu rõ bản chất hình học và cách dựng mặt phẳng phụ hợp lý.
A. Cách xác định và tính số đo góc phẳng nhị diện
Hình vẽ minh họa:
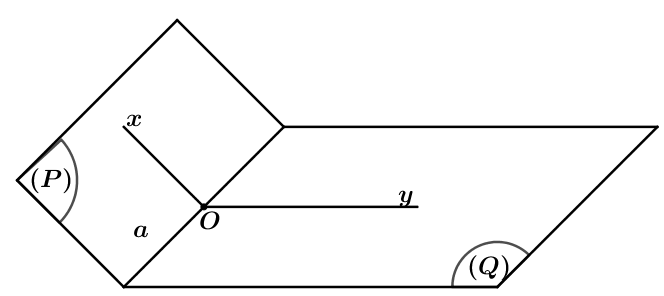
Ta xác định góc nhị diện tạo bởi hai mặt phẳng 
\((P)\) và \((Q)\) theo 3 bước:
-
Bước 1: Tìm giao tuyến
\(a = (P) \cap
(Q)\). -
Bước 2: Tìm
\(x \subset (P):x\bot
a\) và \(y \subset (Q):y\bot
a\). -
Bước 3: Kết luận
\(\lbrack
P,a,Q\rbrack\).
B. Bài tập minh họa tính góc phẳng nhị diện
Ví dụ 1. Cho tứ diện \(S.ABC\) có các cạnh \(SA\), \(SB\), \(SC\) đôi một vuông góc và \(SA = SB = SC = 1\). Gọi \(\alpha\) là góc phẳng nhị diện \(\lbrack
S,BC,A\rbrack\). Tính \(\cos\alpha\)?
Hướng dẫn giải
Hình vẽ minh họa:
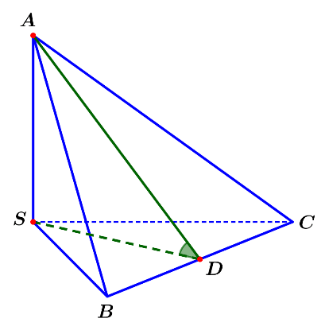
Gọi \(D\) là trung điểm cạnh \(BC\) suy ra \(SD\bot BC\) ( vì tam giác \(SBC\) cân tại \(S\)).
Suy ra \(\left\{ \begin{matrix}
SA\bot SB \\
SA\bot SC
\end{matrix} \right.\ \Rightarrow SA\bot(SBC) \Rightarrow SA\bot
BC\) và \(SD\bot BC\) \(\Rightarrow BC\bot(SAD) \Rightarrow BC\bot
SD\).
Khi đó: \(\left\{ \begin{matrix}
(SBC) \cap (ABC) = BC \\
SD\bot BC \\
AD\bot BC
\end{matrix} \right.\ \Rightarrow \lbrack S,BC,A\rbrack = \widehat{SDA}
= \alpha\).
Xét \(\Delta SAD\) vuông tại \(S\) ta có: \(\cos\alpha = \cos\widehat{SDA} = \frac{SD}{AD} =
\frac{1}{\sqrt{3}}\).
Ví dụ 2: Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông tại \(A\) và \(B\), biết \(AD = 2a\), \(AB =
BC = a\), cạnh bên \(SA\) vuông góc với mặt đáy và \(SA = \frac{{a\sqrt 6 }}{2}\). Gọi \(E\) là trung điểm của \(AD\). Tính số đo của góc phẳng nhị diện \(\lbrack S,BE,A\rbrack\).
Hướng dẫn giải
Hình vẽ minh họa:
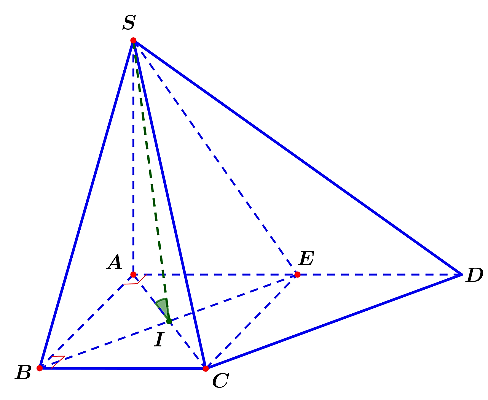
Nhận xét: \(ABCE\) là hình vuông cạnh bằng \(a\). Gọi \(I = AC \cap BE\).
Ta có: \(\left\{ \begin{matrix}
BE\bot AI \\
BE\bot SA
\end{matrix} \right.\ \Rightarrow BE\bot(SAI) \Rightarrow BE\bot
SI\).
Khi đó \(\left\{ \begin{matrix}
(SBE) \cap (ABE) = BE \\
AI\bot BE \\
SI\bot BE
\end{matrix} \right.\ \Rightarrow \lbrack S,BE,A\rbrack =
\widehat{SIA}\)
Xét \(\Delta SIA\) vuông tại \(A\), ta có: \(\tan\widehat{SIA} = \frac{SA}{IA} =
\frac{a\sqrt{6}}{2}:\frac{a\sqrt{2}}{2} = \sqrt{3} \Rightarrow
\widehat{SIA} = 60{^\circ}\).
C. Bài tập tự rèn luyện có hướng dẫn chi tiết
Bài tập 1. Cho hình lăng trụ đứng \(ABC.A'B'C'\) có tất cả các cạnh bằng nhau. Gọi \(\varphi\) số đo của góc phẳng nhị diện \(\lbrack
A',B'C',A\rbrack\). Tính \(\varphi\)?
Bài tập 2. Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông tại \(A\) và \(D\), cạnh bên \(2a\) vuông góc với mặt đáy và \(SA = a\sqrt{2}\). Biết \(AB = 2AD = 2DC = 2a\). Tính số đo của góc phẳng nhị diện \(\lbrack
C,SB,A\rbrack\).
Bài tập 3. Cho hình chóp \(S.ABC\) có cạnh đáy bằng \(3a\) và cạnh bên \(2a\). Tính số đo nhị diện \(\lbrack S,BC,A\rbrack.\)
✨ Bài viết chỉ trích dẫn một phần nội dung, mời bạn tải tài liệu đầy đủ để nắm trọn kiến thức.
------------------------------------------
Khi hiểu đúng bản chất và cách xác định góc phẳng nhị diện, học sinh sẽ giải quyết các bài toán liên quan một cách chính xác và tự tin hơn. Thông qua hệ thống bài tập Toán 11 có đáp án, người học có thể củng cố kiến thức, rèn kỹ năng dựng hình và nâng cao khả năng vận dụng trong các dạng bài góc trong không gian.
