Đơn giản biểu thức G
Rút gọn biểu thức ![]() với
với ![]() ta được kết quả là:
ta được kết quả là:
Ta có:
Cùng nhau thử sức với bài kiểm tra 45 phút Toán 11 Cánh Diều Chương 6: Hàm số mũ và hàm số lôgarit nha!
Đơn giản biểu thức G
Rút gọn biểu thức ![]() với
với ![]() ta được kết quả là:
ta được kết quả là:
Ta có:
Xác định hàm số
Cho đồ thị của hàm số ![]()

Hàm số tương ứng với đồ thị trên là:
Đồ thị hàm số đi qua điểm A(2; 1) nên hàm số tương ứng với đồ thị là:
Tìm hàm số nghịch biến trên tập số thực
Trong các hàm số sau hàm số nào nghịch biến trên tập số thực?
Loại các đáp án và
vì các hàm số trong các đáp án này không xác định trên
.
Vì nên hàm số nghịch biến trên
.
Xác định m để bất phương trình thỏa mãn điều kiện
Tìm giá trị tham số m để bất phương trình ![]() có nghiệm đúng với mọi x.
có nghiệm đúng với mọi x.
Ta có:
Bất phương trình đã cho có nghiệm đúng với mọi x khi cả (1) và (2) đúng với mọi x.
Với hoặc
không thỏa mãn đề bài.
Với hoặc
để thỏa mãn đề bài thì:
Tính giá trị của biểu thức F
Cho biểu thức ![]() . Với
. Với ![]() thì giá trị của biểu thức
thì giá trị của biểu thức ![]() bằng:
bằng:
Ta có:
Thay vào biểu thức F vừa biến đổi ta được:
Chọn khẳng định đúng
Thu gọn biểu thức ![]() ta được kết quả ta được phân số tối giản
ta được kết quả ta được phân số tối giản ![]() . Khẳng định nào sau đây đúng?
. Khẳng định nào sau đây đúng?
Ta có:
Suy ra
Tính tổng của a và b
Giả sử ![]() là các số thực sao cho
là các số thực sao cho ![]() đúng với mọi các số dương
đúng với mọi các số dương ![]() thỏa mãn
thỏa mãn ![]() và
và ![]() . Tính giá trị của
. Tính giá trị của ![]() bằng:
bằng:
Ta có:
Khi đó:
Vậy
Tính giá trị biểu thức H
Giả sử phương trình ![]() có nghiệm là
có nghiệm là ![]() . Tính giá trị biểu thức
. Tính giá trị biểu thức ![]() ?
?
Điều kiện xác định
Phương trình đã cho tương đương:
Nghiệm của phương trình là
Chọn đáp án đúng
Biết ![]() , khi đó
, khi đó ![]() bằng:
bằng:
Ta có:
Tìm hàm số tương ứng đồ thị
Cho đồ thị hàm số:

Xác định hàm số tương ứng?
Đồ thị hàm số đi lên và qua điểm có tọa độ nên hàm số thỏa mãn là
Tìm x
Tìm giá trị của x biết ![]() .
.
Điều kiện
Ta có:
Rút gọn biểu thức
Rút gọn biểu thức ![]() .
.
Ta có:
Tính giá trị biểu thức G
Tính giá trị biểu thức ![]() với a là một số thực dương.
với a là một số thực dương.
Ta có:
Tính giá trị biểu thức
Cho biết ![]() . Tính giá trị biểu thức
. Tính giá trị biểu thức ![]() theo các giá trị
theo các giá trị ![]() ?
?
Ta có:
Ta có:
Tính số tiền anh B phải trả
Anh B vay ngân hàng 200 triệu đồng và trả góp trong vòng 1 năm với lãi suất 1,15%/tháng. Sau đúng một tháng kể từ ngày vay, anh B hoàn nợ cho ngân hàng với số tiền hoàn nợ mỗi tháng là như nhau. Hỏi số tiền gần nhất với số tiền mỗi tháng anh B sẽ phải trả cho ngân hàng là bao nhiêu? Biết lãi suất ngân hàng không thay đổi trong thời gian anh B hoàn nợ.
Mỗi tháng anh B phải trả số tiền cho ngân hàng là:
Chọn đáp án đúng
Giả sử phương trình ![]() có hai nghiệm
có hai nghiệm ![]() với
với ![]() . Khi đó giá trị của biểu thức
. Khi đó giá trị của biểu thức ![]() 2||9||-1||-7
2||9||-1||-7
Giả sử phương trình ![]() có hai nghiệm
có hai nghiệm ![]() với
với ![]() . Khi đó giá trị của biểu thức
. Khi đó giá trị của biểu thức ![]() 2||9||-1||-7
2||9||-1||-7
Điều kiện xác định
Phương trình đã cho tương đương:
Giải phương trình mũ
Xác định nghiệm của phương trình ![]() ?
?
Ta có:
Vậy phương trình có nghiệm là:
Chọn đáp án đúng
Tìm điều kiện của tham số ![]() để phương trình
để phương trình ![]() có nghiệm?
có nghiệm?
Ta có:
Phương trình có nghiệm khi và chỉ khi phương trình
có nghiệm
Xét phương trình
Nếu phương trình vô nghiệm
Nếu có nghiệm
khi và chỉ khi
Vậy thỏa mãn yêu cầu đề bài.
Chọn đáp án đúng
Tổng các nghiệm của phương trình ![]() bằng 3||-3||-4||5
bằng 3||-3||-4||5
Tổng các nghiệm của phương trình ![]() bằng 3||-3||-4||5
bằng 3||-3||-4||5
Ta có:
Vậy tổng các nghiệm của phương trình là 3
Tìm tập nghiệm của bất phương trình
Xác định nghiệm của bất phương trình ![]() ?
?
Ta có:
Vậy tập nghiệm của bất phương trình là
Tìm x để hàm số có nghĩa
Tìm tập xác định của hàm số ![]() ?
?
Điều kiện xác định
Suy ra tập xác định của hàm số là: .
Biểu diễn biểu thức theo a và b
Đặt ![]() . Hãy biểu diễn
. Hãy biểu diễn ![]() theo a và b.
theo a và b.
Ta có:
Tính giá trị biểu thức P
Cho hai số thực dương a và b thỏa mãn ![]() và
và ![]() . Giá trị của biểu thức
. Giá trị của biểu thức ![]() là:
là:
Theo điều kiện ta có:
Tìm hàm số nghịch biến
Tìm hàm số nghịch biến trên tập số thực?
Ta có:
Hàm số có cơ số
nên hàm số nghịch biến trên
Hàm số có tập xác định
nên hàm số đồng biến trên
Hàm số có
nên hàm số nghịch biến trên
.
Hàm số có
nên hàm số đồng biến trên
.
Tính x + y
Cho ![]() . Nếu viết
. Nếu viết ![]() thì giá trị
thì giá trị ![]() bằng bao nhiêu?
bằng bao nhiêu?
Ta có:
Tìm tất cả các giá trị thực a
Cho phương trình ![]() với
với ![]() là tham số. Tìm tất cả các giá trị thực của
là tham số. Tìm tất cả các giá trị thực của ![]() để phương trình đã cho có nghiệm thực?
để phương trình đã cho có nghiệm thực?
Để phương trình có nghiệm thực thì
.
Tìm điều kiện xác định của hàm số
Điều kiện xác định của hàm số ![]() là:
là:
Điều kiện xác định của hàm số là
Tìm tập xác định của hàm số
Trong các hàm số sau đây, hàm số nào có tập xác định ![]() ?
?
Ta có:
Hàm số có tập xác định
Hàm số có tập xác định
Hàm số có tập xác định
Hàm số có tập xác định
Mệnh đề nào sau đây là đúng
Cho biểu thức ![]() với x > 0. Mệnh đề nào sau đây là đúng?
với x > 0. Mệnh đề nào sau đây là đúng?
Ta có:
So sánh P và Q
Cho ![]() và
và ![Q = 2\sqrt {{{\left( {\sqrt[3]{{{x^2}}} + \sqrt[3]{{{y^2}}}} ight)}^3}}](/data/image/holder.png) với x và y là các số thực khác 0. So sánh P và Q?
với x và y là các số thực khác 0. So sánh P và Q?
Ta có: là những số thực dương
Ta lại có:
Giá trị của biểu thức
Giá trị của biểu thức ![]() bằng:
bằng:
Ta có:
Tìm x
Cơ số x bằng bao nhiêu để ![]() ?
?
Điều kiện
Ta có:
Vậy là giá trị cần tìm.
Tìm giá trị của m
Biết ![\sqrt[5]{{\frac{b}{a}\sqrt[3]{{\frac{a}{b}}}}} = {\left( {\frac{a}{b}} ight)^m}](/data/image/holder.png) với a và b là các số thực dương. Tìm m?
với a và b là các số thực dương. Tìm m?
Ta có:
Tính giá trị biểu thức
Cho ![]() khi đó
khi đó ![]() có giá trị bằng bao nhiêu?
có giá trị bằng bao nhiêu?
Ta có:
Chọn đáp án đúng
Một người gửi vào ngân hàng 200 triệu đồng vào tài khoản tiết kiệm ngân hàng với lãi suất 0,6%/ tháng, cứ sau mỗi tháng người đó rút ra 500 nghìn đồng. Hỏi sau đúng 36 lần rút tiền thì số tiền còn lại trong tài khoản của người đó gần nhất với phương án nào sau đây? (Biết rằng lãi suất không thay đổi và tiền lại mỗi tháng tính theo số tiền thực tế trong tài khoản của tháng đó?
Số tiền còn lại trong tài khoản sau tháng thứ 1 là: (triệu đồng)
Số tiền còn lại trong tài khoản sau tháng thứ 2 là:
(triệu đồng)
Số tiền còn lại trong tài khoản sau tháng thứ 3 là:
(triệu đồng)
Cứ tiếp tục quá trình thì số tiền còn lại trong tài khoản sau tháng thứ 36 là:
(triệu đồng).
Xét tính đúng sai của các khẳng định
Vẽ được đồ thị của các hàm số sau. Các khẳng định dưới đây đúng hay sai?
a) Đồ thị ![]() có dạng bên:
có dạng bên: 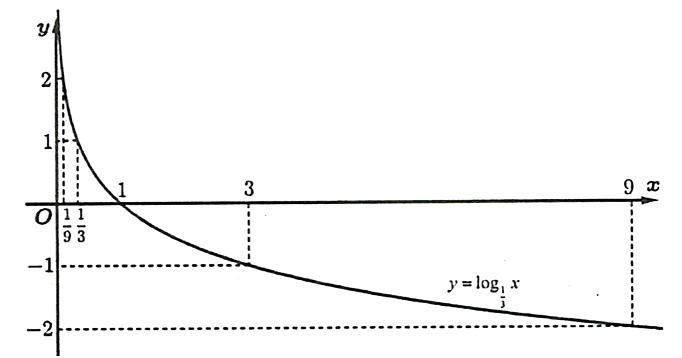 . Đúng||Sai
. Đúng||Sai
b) Đồ thị ![]() có dạng bên:
có dạng bên: 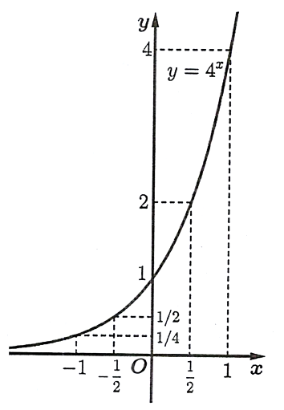 . Đúng||Sai
. Đúng||Sai
c) Đồ thị ![]() có dạng bên:
có dạng bên: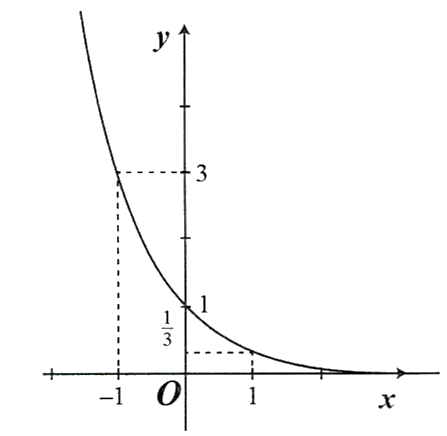 . Đúng||Sai
. Đúng||Sai
b) Đồ thị ![]() có dạng bên:
có dạng bên: 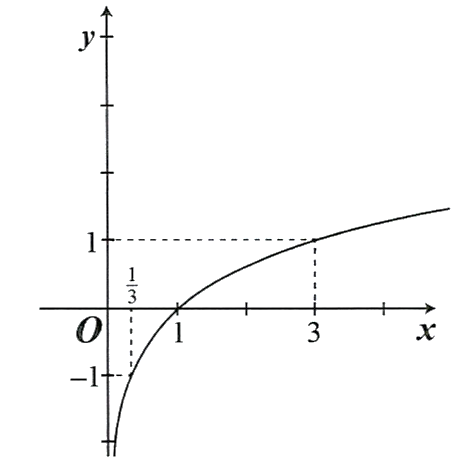 . Đúng||Sai
. Đúng||Sai
Vẽ được đồ thị của các hàm số sau. Các khẳng định dưới đây đúng hay sai?
a) Đồ thị ![]() có dạng bên:
có dạng bên:  . Đúng||Sai
. Đúng||Sai
b) Đồ thị ![]() có dạng bên:
có dạng bên:  . Đúng||Sai
. Đúng||Sai
c) Đồ thị ![]() có dạng bên:
có dạng bên: . Đúng||Sai
. Đúng||Sai
b) Đồ thị ![]() có dạng bên:
có dạng bên:  . Đúng||Sai
. Đúng||Sai
|
a) Đúng |
b) Đúng |
c) Đúng |
d) Đúng |
a) Hàm số có bảng giá trị:

Đồ thị của hàm số :
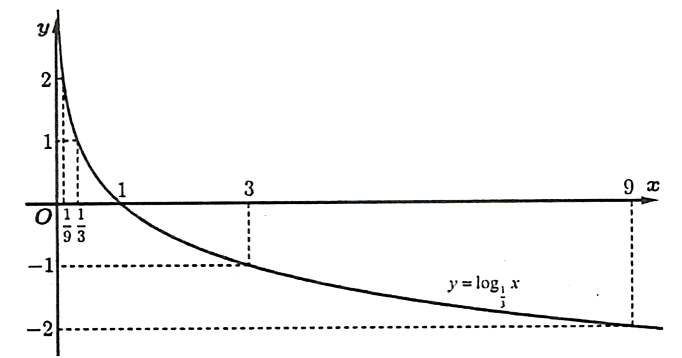
b) Hàm số có bảng giá trị:

Đồ thị của hàm số :
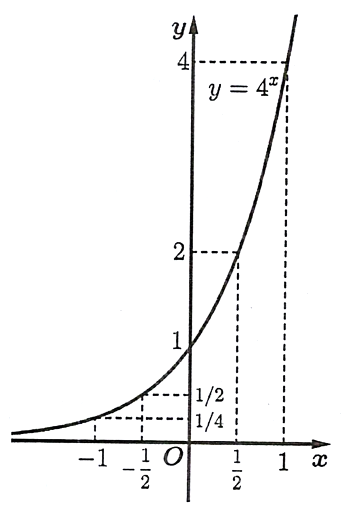
c) Hàm số nghịch biến trên
. Hàm số qua các điểm
,
và nằm trên trục hoành. Đồ thị:
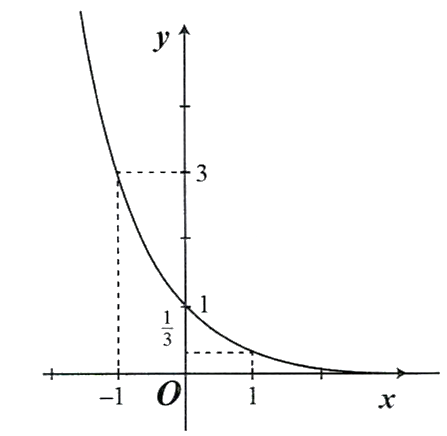
d) Hàm số đồng biến trên
. Hàm số qua các điểm
,
và nằm bên phải trục tung. Đồ thị:
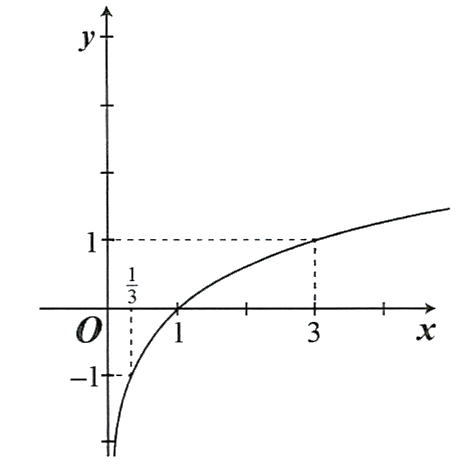
Giải bất phương trình mũ
Xác định tập nghiệm của bất phương trình ![]() ?
?
Ta có:
Vậy tập nghiệm bất phương trình là
Tính giá trị biểu thức
Biết ![]() . Tính
. Tính ![]() ?
?
Ta có:
Chọn khẳng định đúng
Cho a và b là các số thực thỏa mãn điều kiện ![]() và
và ![]() . Chọn khẳng định đúng trong các khẳng định sau:
. Chọn khẳng định đúng trong các khẳng định sau:
Ta có:
Tính giá trị biểu thức D
Tính giá trị biểu thức ![]() .
.
Ta có:
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
