Hình lăng trụ đứng. Hình chóp đều. Thể tích của một số hình khối Cánh Diều
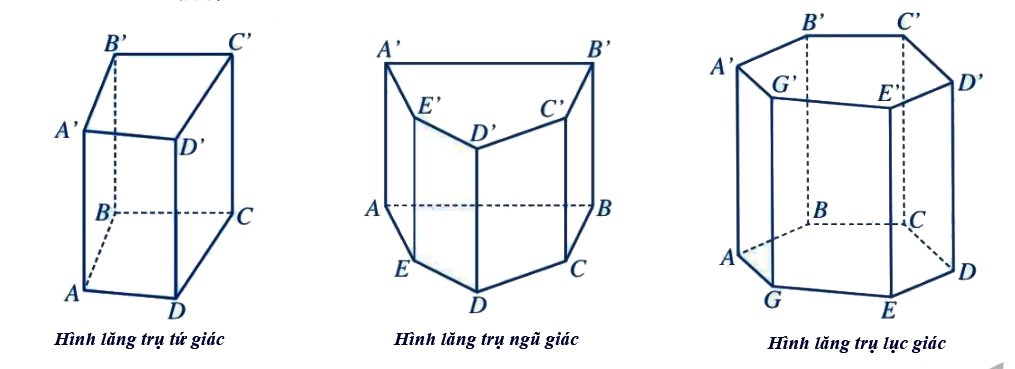
Hình lăng trụ đứng là hình lăng trụ có các cạnh bên vuông góc với mặt đáy.
- Hình lăng trụ đứng có đáy là đa giác đều gọi là hình lăng trụ đều.
- Hình lăng trụ đứng có đáy là hình bình hành gọi là hình hộp đứng.
- Khi đáy của các lăng trụ đứng là tứ giác, ngũ giác, lúc giác, … ta gọi hình lăng trụ đứng đó là hình lăng trụ đứng tứ giác, hình lăng trụ đứng ngũ giác, hình lăng trụ đứng lục giác, …
Minh họa
Nhận xét:
- Mỗi mặt bên của hình lăng trụ đứng là hình chữ nhật, mặt phẳng chứa nó vuông góc với mặt đáy.
- Hình hộp chữ nhật là một hình hộp đứng có đáy là hình chữ nhật.
- Hình hộp chữ nhật có 6 mặt là hình chữ nhật.
- Nếu mỗi mặt của hình hộp là hình chữ nhật thì hình hộp đó là hình hộp chữ nhật.
- Độ dài đường chéo của hình hộp chữ nhật là bằng nhau.
- Hình lập phương là hình hộp chữ nhật có tất cả các mặt là hình vuông.
- Nếu các mặt của một hình hộp chữ nhật có diện tích bằng nhau thì hình hộp chữ nhật đó là hình lập phương.
II. Hình chóp đều. Hình chóp cụt đều
a) Hình chóp đều
Hình chóp đều là hình chóp có đáy là đa giác đều và các cạnh bên bằng nhau.
Minh họa
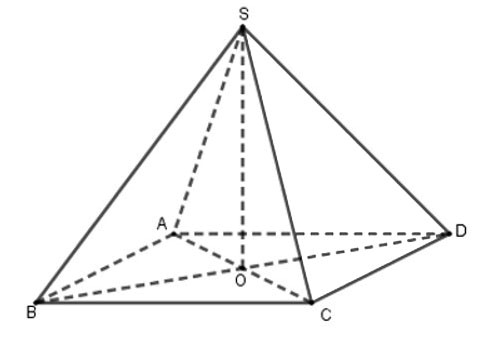
Ví dụ: Hình chóp tứ giác có đáy là hình vuông và các cạnh bên bằng nhau là hình chóp tứ giác đều.
Chú ý:
- Khi đáy của hình chóp đều lần lượt là tam giác đều, hình vuông, ngũ giác đều, ta gọi hình chóp đó lần lượt là hình chóp tam giác đều, hình chóp tứ giác đều, hình chóp ngũ giác đều, hình chóp lục giác đều.
- Hình chóp tam giác đều có cạnh bên bằng cạnh đáy là tứ diện đều.
Chân đường cao của hình chóp đều là tâm đường tròn ngoại tiếp của đáy.
b) Hình chóp cụt đều
Hình gồm các đa giác đều 
\(A_{1}A_{2}A_{3}...A_{n}.B_{1}B_{2}B_{3}...B_{n}\) và các hình thang cân \(A_{1}A_{2}B_{1}B_{2};A_{2}A_{3}B_{3}B_{2};\) … \(A_{n}A_{1}B_{1}B_{n}\) được tạo thành như trong hình vẽ được gọi là hình chóp cụt đều (nói đơn giản là hình chóp cụt được tạo thành từ hình chóp đều \(S.A_{1}A_{2}A_{3}...A_{n}\) sau khi cắt đi chóp đều \(S.B_{1}B_{2}B_{3}...B_{n}\) ), kí hiệu là \(A_{1}A_{2}A_{3}...A_{n}.B_{1}B_{2}B_{3}...B_{n}\) .
Hình vẽ minh họa
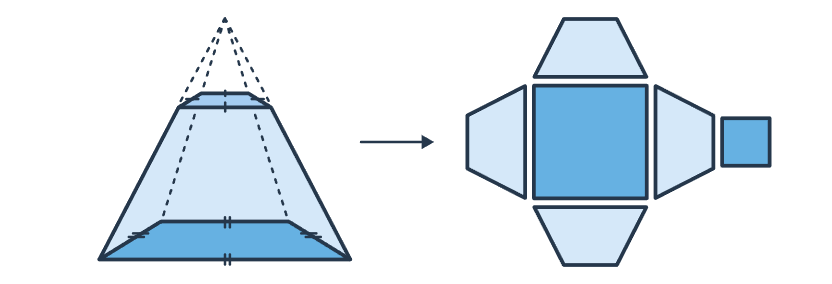
Đặc điểm hình chóp cụt đều
- Các đa giác \(A_{1}A_{2}A_{3}...A_{n};B_{1}B_{2}B_{3}...B_{n}\) được gọi là hai mặt đáy, các hình thang \(A_{1}A_{2}B_{1}B_{2};A_{2}A_{3}B_{3}B_{2};\) …; \(A_{n}A_{1}B_{1}B_{n}\) được gọi là mặt bên của hình chóp cụt.
- Các đoạn thẳng \(A_{1}B_{1};A_{2}B_{2};...;A_{n}B_{n}\) được gọi là các cạnh bên, cạnh của các mặt đáy được gọi là các cạnh đáy của hình chóp cụt.
- Đoạn thẳng nối hai tâm của đáy được gọi là đường cao của hình chóp cụt đều. Độ dài của đường cao được gọi là chiều cao của hình chóp.
Nhận xét:
- Hai đáy của hình chóp cụt đều nằm trên hai mặt phẳng song song và có các cạnh tương ứng song song: đồng thời hai đáy đó là các đa giác đều có cùng số cạnh.
- Mỗi mặt bên của hình chóp cụt đều là một hình thang cân.
- Các đường thẳng chứa cạnh bên của hình chóp cụt đều cùng đi qua một điểm.
- Đường cao của hình chóp cụt đều thì vuông góc với hai đáy của hình chóp cụt đều đó.
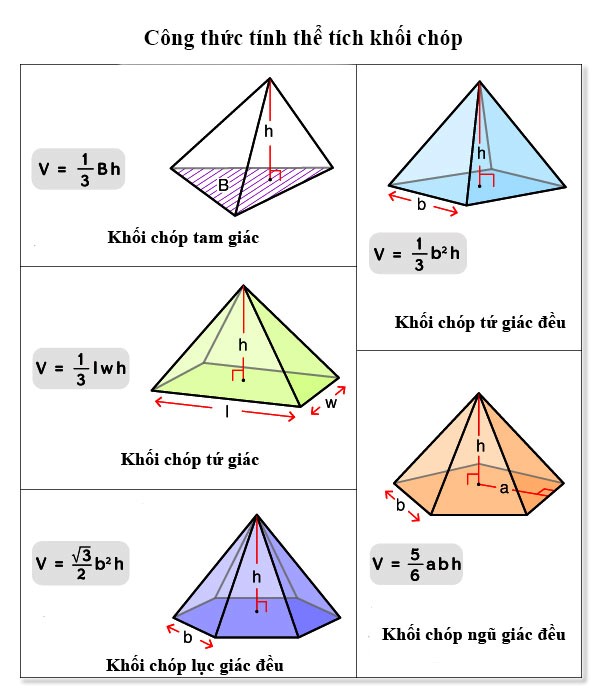
III. Thể tích của một số hình khối
|
Thể tích |
Phát biểu |
Minh họa |
Công thức |
|
Khối hộp chữ nhật |
Bằng diện tích đáy nhân với chiều cao |
 |
\(V = a.b.c\) |
|
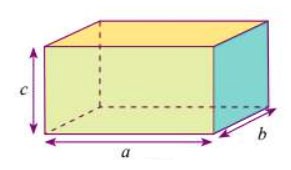Khối chóp |
Bằng một phần ba diện tích đáy nhân với chiều cao |
 |
\(V = \frac{1}{3}.S.h\) |
|
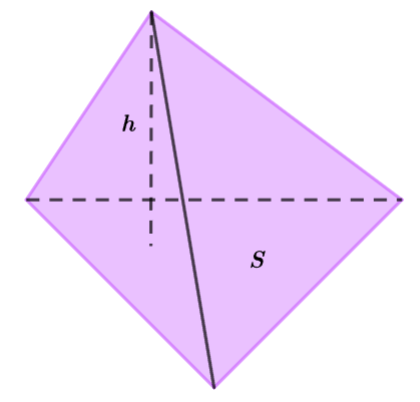Khối lăng trụ |
Bằng diện tích đáy nhân với chiều cao |
 |
\(V = S.h\) |
|
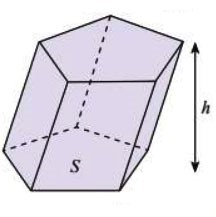Khối chóp cụt đều |
|
 |
\(V = \frac{1}{3}.h.\left( S + S' +
\sqrt{S.S'} \right)\) |
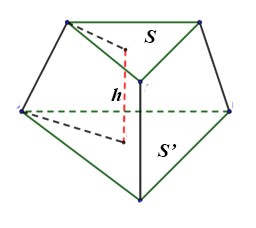Công thức mở rộng
