Đường thẳng và mặt phẳng song song Cánh Diều
Có ba khả năng xảy ra đối với số điểm chung của d và (P):
|
|
Số điểm chung |
Kí hiệu |
Minh họa |
|
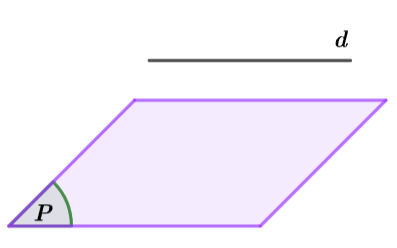
d nằm trong (P) |
 \(\geq 2\) |
\(d \subset (P),(P) \supset
d\) |
 |
|
d cắt (P) |
\(1\) |
\(d \cap (P) = \left\{ A
\right\}\) |
 |
|
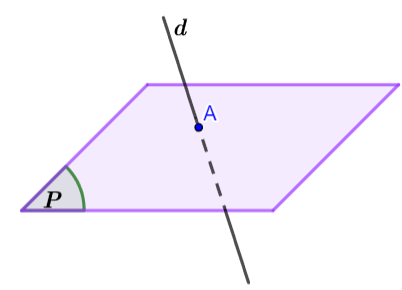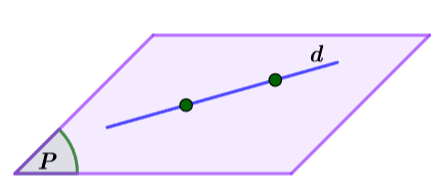
d song song với (P) |
\(0\) |
\(d//(P)\) |
 |
Đường thẳng được gọi là song song với mặt phẳng nếu chúng không có điểm chung.
Ví dụ: Cho hình chóp \(S.ABCD\), đáy \(ABCD\) là hình bình hành. Gọi \(M, N\) lần lượt là trung điểm các cạnh \(SA\) và \(CD\). Chứng minh \(MN // (SBC)\).
Hướng dẫn giải
Hình vẽ minh họa
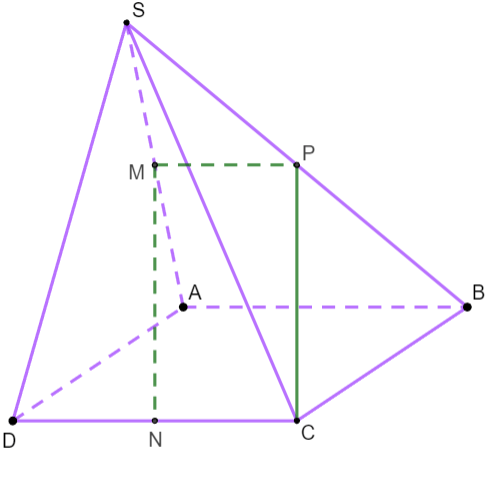
Xét tam giác \(SAB\), gọi P là trung điểm của \(SB\) khi đó ta có
\(MP\) là đường trung bình của tam giác
=> \(MP//AB;MP = \frac{1}{2}AB\) (*)
Lại có \(AB//CD,AB = CD\)
=> \(CN//AB;CN = \frac{1}{2}AB\) (**)
Từ (*) và (**) suy ra \(MP//CN,MP =
CN\)
=> Tứ giác \(MNCP\) là hình bình hành.
=> \(MN//CP \subset (SBC)\)
=> \(MN//(SBC)\) (điều phải chứng minh)
2. Điều kiện và tính chất
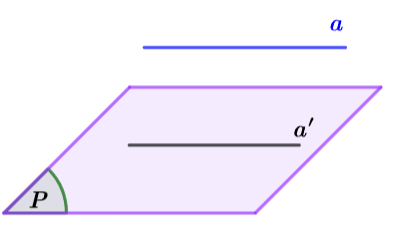
Định lí 1 (dấu hiệu nhận biết đường thẳng song song với mặt phẳng)
Nếu đường thẳng a không nằm trong mặt phẳng (P) và a song song với đường thẳng a’ nằm trong (P) thì a song song với mặt phẳng (P).
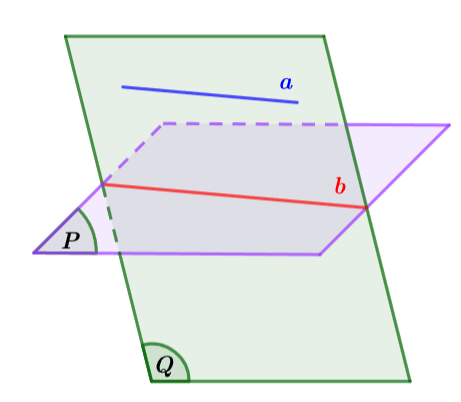
Định lí 2 (Tính chất đường thẳng song song với mặt phẳng)
Cho đường thẳng a song song với mặt phẳng (P). Nếu mặt phẳng (Q) chứa a và cắt (P) theo giao tuyến b thì b song song với a.
Hệ quả
Nếu hai mặt phẳng phân biệt cùng song song với một đường thẳng thì giao tuyến của chúng (nếu có) cũng song song với đường thẳng đó.
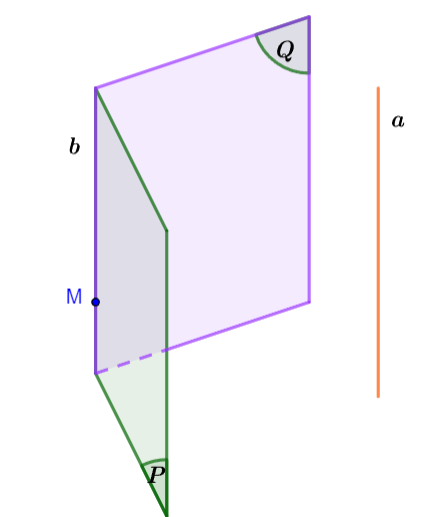
Chú ý: Cho hai đường thẳng chéo nhau. Khi đó có duy nhất một mặt phẳng chứa đường thẳng này và song song với đường thẳng kia.
Ví dụ: Cho hình chóp \(S.ABCD\) có đáy là hình thang cạnh đáy là \(AB\) và \(CD\). Gọi \(I, J\) lần lượt là trung điểm của \(AD\) và \(BC\), \(G\) là trọng tâm của tam giác \(SAB\). Tìm giao tuyến của hai mặt phẳng \((SAB)\) và \((IJG)\).
Hướng dẫn giải
Hình vẽ minh họa
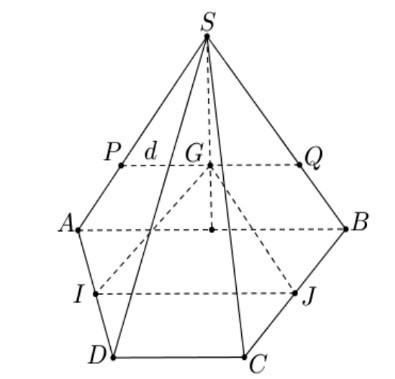
Ta có: \(I, J\) lần lượt là trung điểm của \(AD\) và \(BC\).
=> \(IJ\) là đường trung bình của hình thang ABCD
=> \(IJ // AB // CD\)
Gọi \(d = (SAB) \cap (IJG)\)
Ta có \(G\) là điểm chung của hai mặt phẳng \((SAB)\) và \((IJG)\).
Mặt khác \(\left\{ \begin{matrix}
AB \subset (SAB);IJ \subset (IJG) \\
AB//IJ \\
\end{matrix} \right.\)
=> Giao tuyến của hai mặt phẳng \((SAB)\) và \((IJG)\) là đường thẳng qua \(G\) và song song với \(AB\) và \(IJ\) (đường thẳng \(PQ\)).
