Khoảng cách Cánh Diều
Cho đường thẳng 
\(\Delta\) và điểm \(M \notin \Delta\). Gọi \(H\) là hình chiếu của điểm \(M\) trên đường thẳng \(\Delta\).
Độ dài đoạn thẳng \(MH\) gọi là khoảng cách từ điểm \(M\) đến đường thẳng \(\Delta\). Kí hiệu \(d(M,\Delta)\).
Minh họa
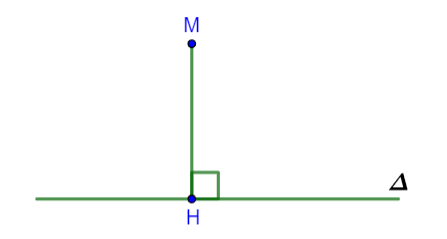
Chú ý: \(M \in \Delta
\Rightarrow d(M,\Delta) = 0\).
II. Khoảng cách từ một điểm đến một mặt phẳng
Cho mặt phẳng \((P)\) và điểm \(M \notin (P)\). Gọi \(H\) là hình chiếu của \(M\) trên mặt phẳng \((P)\).
Độ dài đoạn thẳng \(MH\) gọi là khoảng cách từ điểm \(M\) đến mặt phẳng \((P)\). Kí hiệu \(d\left( M,(P) \right)\).
Minh họa
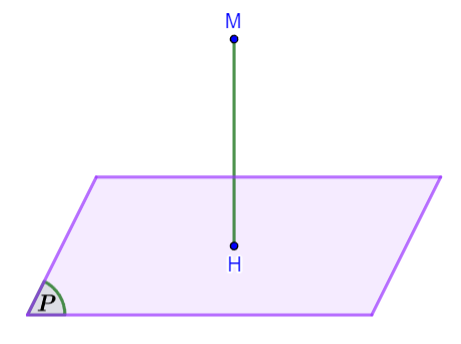
Chú ý: \(M \in (P)
\Rightarrow d\left( M,(P) \right) = 0\).
III. Khoảng cách giữa hai đường thẳng song song
Khoảng cách giữa hai đường thẳng song song \(\Delta,\Delta'\) là khoảng cách từ một điểm bất kì thuộc đường thẳng này đến đường thẳng kia. Kí hiệu \(d(\Delta,\Delta')\).
Minh họa
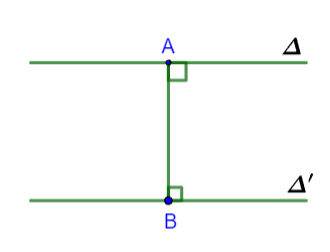
IV. Khoảng cách giữa đường thẳng và mặt phẳng song song
Cho đường thẳng \(\Delta\) song song với mặt phẳng \((P)\). Khoảng cách giữa đường thẳng \(\Delta\) và mặt phẳng \((P)\) là khoảng cách từ một điểm bất kì thuộc đường thẳng \(\Delta\) đến mặt phẳng \((P)\). Kí hiệu \(d\left( \Delta,(P) \right)\).
Minh họa
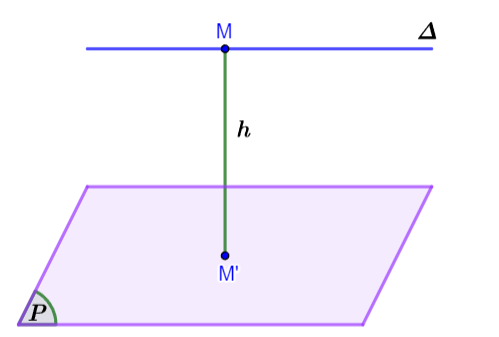
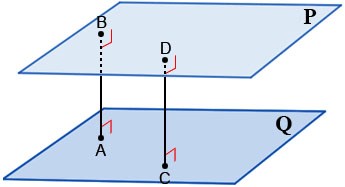
V. Khoảng cách giữa hai mặt phẳng song song
Khoảng cách giữa hai mặt phẳng song song \((P),(Q)\) là khoảng cách từ một điểm bất kì thuộc mặt phẳng này đến mặt phẳng kia. Kí hiệu \(d\left( (Q),(P) \right)\).
Minh họa
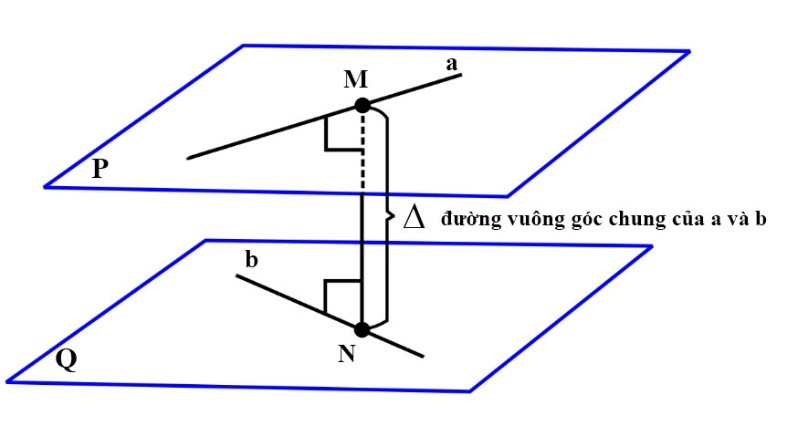
VI. Khoảng cách giữa hai đường thẳng chéo nhau
Cho hai đường thẳng \(a,b\) chéo nhau.
- Đường thẳng \(c\) vừa vuông góc, vừa cắt cả hai đường thẳng \(a,b\) được gọi là đường vuông góc chung của hai đường thẳng đó.
- Đoạn thẳng có hai đầu mút là giao điểm của đường thẳng \(c\) và hai đường thẳng \(a,b\) được gọi là đoạn vuông góc chung của hai đường thẳng đó.
- Độ dài đoạn vuông góc chung của hai đường thẳng \(a,b\) được gọi là khoảng cách giữa hai đường thẳng dó. Kí hiệu \(d(a,b)\).
Minh họa
Ví dụ: Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(a\). Tính:
| a) \(d(AB;C'D')\). |
b) \(d\left( AC;(A'B'C'D')
\right)\). |
| c) \(d(A;B'D')\). |
d) \(d(AC;B'D')\). |
Hướng dẫn giải
Hình vẽ minh họa
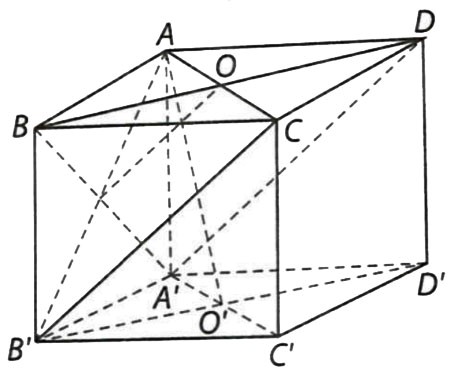
a) Vì B’C’ vuông góc với cả hai đường thẳng AB và C’D’ nên \(d(AB;C'D') = B'C' =
a\sqrt{2}\).
b) Vì \(AC//(A'B'C'D')\) nên \(d\left( AC;(A'B'C'D') \right) =
d\left( A;(A'B'C'D') \right) = AA' = a\).
c) Gọi O’ là giao điểm của \(A'C';B'D'\), ta có: \(AO'\bot B'D'\)
Theo định lí Pythagore cho tam giác \(AA'O'\) vuông tại \(A'\) thì \(AO' = \frac{a\sqrt{6}}{2}\)
Do đó: \(d(A;B'D') = AO' =
\frac{a\sqrt{6}}{2}\).
d) Ta có:
\(d(AC;B'D') = d\left(
AC;(A'B'C'D') \right) = d\left(
A;(A'B'C'D') \right) = AA' = a\).
