Đường thẳng vuông góc với mặt phẳng Cánh Diều
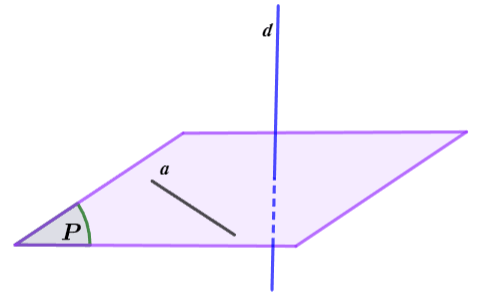
Đường thẳng 
\(d\) được gọi là vuông góc với mặt phẳng \((P)\) nếu đường thẳng \(d\) vuông góc với mọi đường thẳng \(a\) trong mặt phẳng \((P)\).
Kí hiệu: \(d\bot(P)\) hoặc \((P)\bot d\).
Minh họa
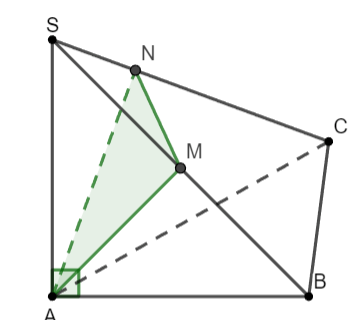
Ví dụ: Cho hình chóp \(S.ABC\) có \(\Delta ABC\) vuông tại \(B\) và \(SA\bot(ABC)\). Kẻ \(AM\bot SB,(M \in SB)\), \(AN\bot SC,(N \in SC)\). Chứng minh rằng:
a) \(BC\bot(SAB)\)
b) \(AM\bot(SBC)\)
c) \(SC\bot(AMN)\)
Hướng dẫn giải
Hình vẽ minh họa
a) Ta có: \(SA\bot(ABC) \Rightarrow SA\bot
AB\)
Ta có: \(\left\{ \begin{gathered}
AB \bot BC \hfill \\
SA \bot BC \hfill \\
AB,SA \subset \left( {SAB} \right) \hfill \\
AB \cap SA = \left\{ A \right\} \hfill \\
\end{gathered} \right. \Rightarrow BC \bot \left( {SAB} \right)\)
b) Ta có: \(BC\bot(SAB)\) và \(AM \subset (SAB)\) nên \(BC\bot AM\)
Mà \(SB\bot AM\) khi đó: \(\left\{ \begin{gathered}
BC \bot AM \hfill \\
SB \bot AM \hfill \\
BC,SB \subset \left( {SBC} \right) \hfill \\
BC \cap SB = \left\{ B \right\} \hfill \\
\end{gathered} \right. \Rightarrow AM \bot \left( {SBC} \right)\)
c) Vì \(AM\bot(SBC)\) và \(SC \subset (SBC)\) \(\Rightarrow AM\bot SC\)
Mà \(AN\bot SC\) khi đó: \(\left\{ \begin{gathered}
AM \bot SC \hfill \\
AN \bot SC \hfill \\
AM,AN \subset \left( {AMN} \right) \hfill \\
AM \cap AN = \left\{ A \right\} \hfill \\
\end{gathered} \right. \Rightarrow SC \bot \left( {AMN} \right)\)
II. Điều kiện để đường thẳng vuông góc với mặt phẳng
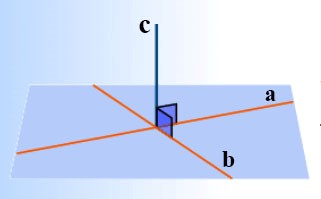
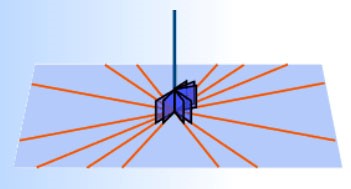
Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau cùng thuộc một mặt phẳng thì nó vuông góc với mặt phẳng ấy.
Minh họa
 |
 |
III. Tính chất
|
Tính chất 1 Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước. Tính chất 2 Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước. |
Minh họa
|
IV. Liên hệ giữa quan hệ song song và quan hệ vuông góc của đường thẳng và mặt phẳng
Tính chất 3
Cho hai đường thẳng song song. Một mặt phẳng vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia.
Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
Tính chất 4
Nếu đường thẳng \(\Delta\) vuông góc với mặt phẳng \((P)\) thì \(\Delta\) vuông góc với mọi đường thẳng song song với \((P)\).
Nếu đường thẳng \(a\) và mặt phẳng \((P)\) cùng vuông góc với một đường thẳng \(\Delta\) thì \(a\) nằm trong \((P)\) hoặc song song với \((P)\).
V. Phép chiếu vuông góc
Cho mặt phẳng \((P)\). Quy tắc đặt tương ứng mỗi điểm \(M\) trong không gian với hình chiếu vuông góc \(M'\) của điểm đó lên mặt phẳng \((P)\) được gọi là phép chiếu vuông góc lên mặt phẳng \((P)\).
Minh họa
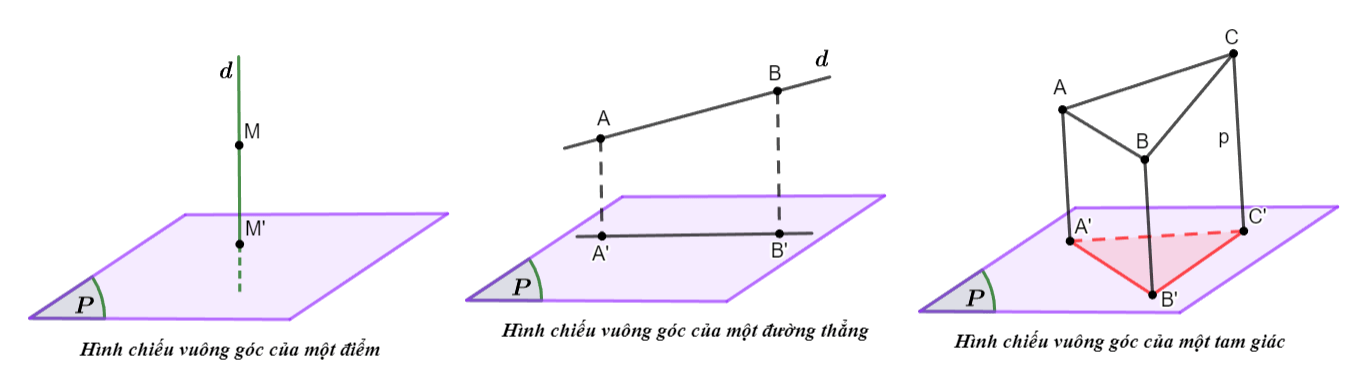
Chú ý: Vì phép chiếu vuông góc là một trường hợp đặc biệt của phép chiếu song song (khi phương chiếu vuông góc với mặt phẳng chiếu) nên phép chiếu vuông góc có đầy đủ tính chất của phép chiếu song song.
VI. Định lí ba đường vuông góc
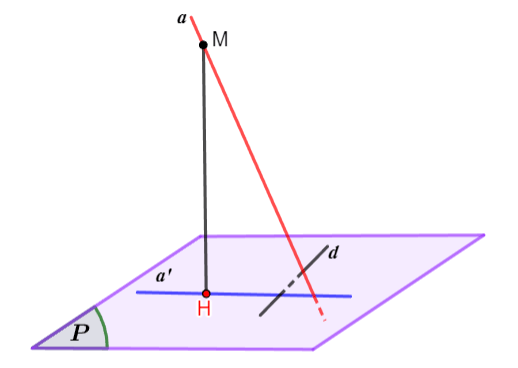
Cho đường thẳng \(a\) không vuông góc với mặt phẳng \((P)\) và đường thẳng \(d\) nằm trong mặt phẳng \((P)\). Khi đó, \(d\) vuông góc với \(a\) khi và chỉ khi \(d\) vuông góc với hình chiếu \(a'\) của \(a\) trên \((P)\).
Minh họa
Ví dụ: Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh a, \(SA = a\sqrt{6}\) và \(SA\) vuông góc \((ABCD)\). Hãy xác định các góc giữa:
a) \(SC\) và \((ABCD)\)
b) \(SC\) và \((SAB)\)
Hướng dẫn giải
Hình vẽ minh họa
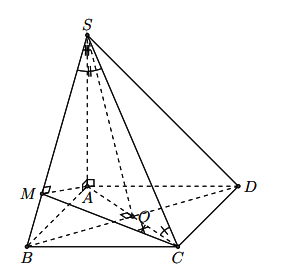
a) Vì \(AC\) là hình chiếu vuông góc của \(SC\) lên \((ABCD)\)
=> Góc giữa \(SC\) và \((ABCD)\) là \(\widehat{SCA}\)
Trong tam giác SCA, ta có:
\(\tan \widehat {SCA} = \frac{{SA}}{{SC}} = \sqrt 3\)
\(\Rightarrow \left( {SC;\left( {ABCD} \right)} \right) = \widehat {SCA} = {60^0}\)
b) Vì \(BC ⊥ (SAB)\) tại B nên SB là hình chiếu vuông góc của \(SC\) lên \((SAB)\)
=> \(\left( SC,(SAB) \right) = (SC,SB) =
\widehat{CSB}\)
Trong tam giác SCB, ta có:
\(\tan \widehat {SCB} = \frac{{BC}}{{SB}} = \frac{a}{{a\sqrt 7 }}\)
\(\Rightarrow \left( {SC;\left( {SAB} \right)} \right) = \arctan \frac{1}{{\sqrt 7 }}\)
