Hai đường thẳng vuông góc Cánh Diều
Góc giữa hai đường thẳng 
\(a\) và \(b\) trong không gian là góc giữa hai đường thẳng \(a'\) và \(b'\) cùng đi qua một điểm \(O\) và lần lượt song song (hoặc trùng) với \(a\) và \(b\).
Kí hiệu \((a,b)\) hoặc \(\widehat{(a,b)}\).
Nhận xét:
- Góc giữa hai đường thẳng \(a,b\) không phụ thuộc vào vị trí điểm \(O\).
- Góc giữa hai đường thẳng \(a,b\) bằng góc giữa hai đường thẳng \(b,a\) tức là: \(\widehat{(a,b)} =
\widehat{(b,a)}\).
- Góc giữa hai đường thẳng không vượt quá \(90^{0}\).
- Nếu \(a//b\) thì \(\widehat{(a,c)} = \widehat{(b,c)}\) với mọi đường thẳng \(c\) trong không gian.
Ví dụ: Cho tứ diện đều \(ABCD\), \(M\) trung điểm của các cạnh \(BC\). Xác định góc giữa hai đường thẳng \(AB\) và \(DM\).
Hướng dẫn giải
Hình vẽ minh họa
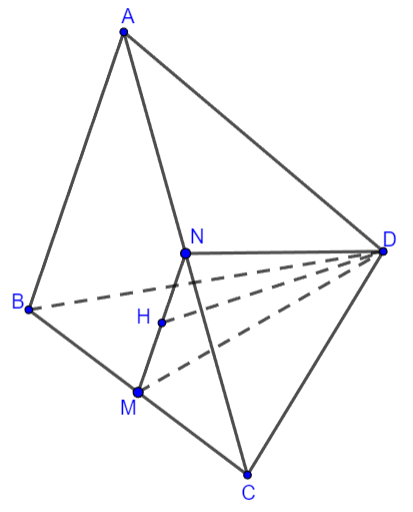
Gọi độ dài cạnh của tứ diện đều là \(2a\)
Gọi \(N\) là trung điểm cạnh \(AC\), \(H\) là trung điểm của \(MN\), ta có:
\(MN//AB \Rightarrow (AB,DM) =
(MN,DM)\)
Vì \(\left\{ \begin{matrix}
DM = DN = a\sqrt{3} \\
MN = a \\
\end{matrix} \right.\) nên tam giác \(DMN\) cân tại \(D\).
\(\Rightarrow MH = \frac{a}{2};DH\bot
MN\)
\(\cos\widehat{DMN} = \frac{MH}{MD} =
\frac{\sqrt{3}}{6} \Rightarrow \widehat{DMN} \approx
73,2^{0}\)
Vậy \((AB,DM) = (MN,DM) = \widehat{DMN}
\approx 73,2^{0}\).
II. Hai đường thẳng vuông góc trong không gian
Hai đường thẳng được gọi là vuông góc với nhau nếu góc giữa chúng bằng \(90^{0}\).
Nhận xét: Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng còn lại.
Ví dụ: Cho hình chóp \(S.ABCD\) có đáy là hình vuông \(ABCD\) cạnh bằng \(a\) và các cạnh bên đều bằng \(a\). Gọi \(M,N\) lần lượt là trung điểm của \(AD,SD\). Chứng minh rằng \(MN\bot SC\).
Hướng dẫn giải
Hình vẽ minh họa
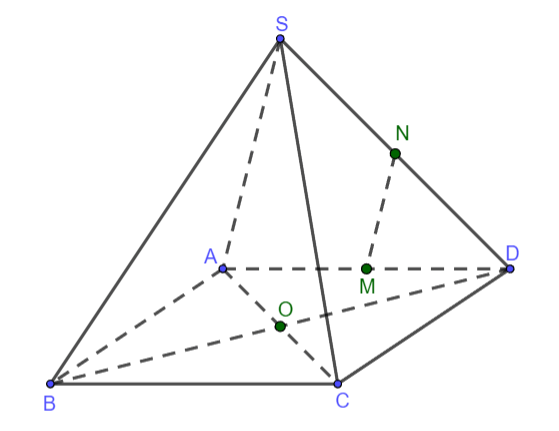
Xét tam giác \(SAD\) có \(M,N\) lần lượt là trung điểm các cạnh \(AD,SD\)
Suy ra \(MN\) là đường trung bình của tam giác \(SAD\)
\(\Rightarrow MN//SA\)
Vậy \((MN,SC) = (SA,SC)\)
Ta có tam giác \(ABC\) vuông tại \(B\) nên \(AC = \sqrt{BC^{2} + AB^{2}} =
a\sqrt{2}\)
Xét tam giác \(SAC\) nhận thấy \(AC^{2} = SA^{2} + SC^{2}\)
Theo định lí Pythagore đảo ta suy ra tam giác \(SAC\) vuông tại \(S\).
\(\Rightarrow \widehat{ASC} =
90^{0}\) hay \((MN,SC) = \widehat{ASC}
= 90^{0}\)
Vậy \(MN\bot SC\).
