Góc giữa đường thẳng và mặt phẳng. Góc nhị diện Cánh Diều
Cho đường thẳng 
\(d\) và mặt phẳng \((P)\) ta có các định nghĩa sau:
- Nếu đường thẳng \(d\) vuông góc với mặt phẳng \((P)\) thì góc giữa \(d\) và \((P)\) bằng \(90^{0}\).
- Nếu đường thẳng \(d\) không vuông góc với mặt phẳng \((P)\) thì góc giữa \(d\) và \((P)\) là góc giữa \(d\) và hình chiếu \(d'\) của đường thẳng \(d\) trên \((P)\).
Minh họa
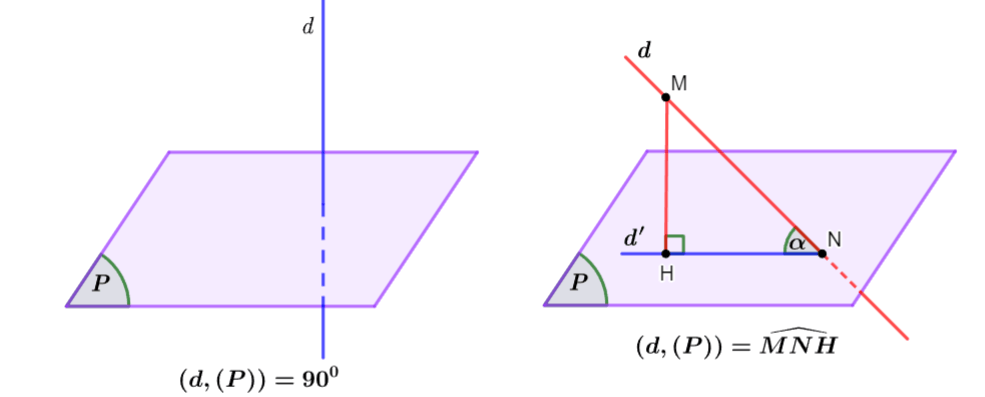
Nhận xét: Góc giữa đường thẳng và mặt phẳng có số đo từ \(0^{0}\) đến \(90^{0}\).
Ví dụ: Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông cân tại \(B\), \(AB =
a;SA\bot(ABC);SA = a\). Tính số đo góc giữa \(SB\) và \((SAC)\)?
Hướng dẫn giải
Hình vẽ minh họa
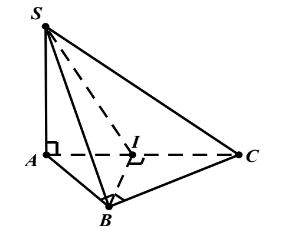
Gọi I là trung điểm AC. Tam giác ABC vuông cân tại B nên \(BI\bot AC\)
Có \(BI\bot SA\) do \(SA\bot(ABC)\) suy ra \(BI\bot(SAC)\)
Do vậy SI là hình chiếu vuông góc của SB lên (SAC).
Khi đó:
\(\left( SB;(SAC) \right) = (SB;SI) =
\widehat{BSI}\)
Xét tam giác SBI vuông tại I (do \(BI\bot(SAC) \Rightarrow BI\bot SI\))
\(SB = \sqrt{SA^{2} + AB^{2}} =
a\sqrt{2}\)
\(SI = \sqrt{SA^{2} + AI^{2}} =
\frac{a\sqrt{6}}{2}\)
\(\cos S = \frac{SI}{SB} =
\frac{\sqrt{3}}{2} \Rightarrow \widehat{BSI} = 30^{0}\)
Vậy \(\left( SB;(SAC) \right) =
30^{0}\).
II. Góc nhị diện
1. Định nghĩa góc nhị diện
Góc nhị diện là hình gồm hai nửa mặt phẳng có chung bờ.
Minh họa
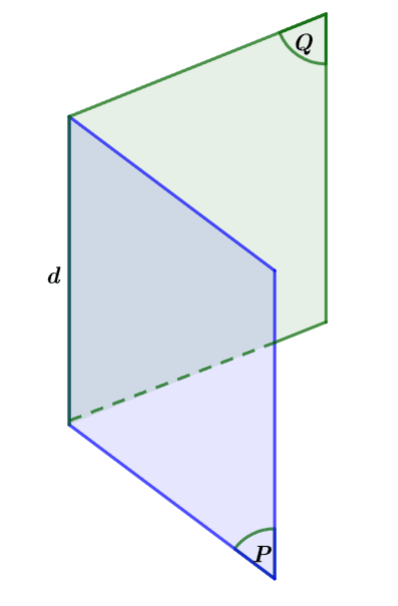
Đường thẳng \(d\) được gọi là cạnh của góc nhị diện, mỗi nửa mặt phẳng \((P)\) và \((Q)\) gọi là một mặt của góc nhị diện. Kí hiệu là \(\lbrack P,d,Q\rbrack\).
Chú ý: Góc nhị diện còn được kí hiệu là \(\lbrack A,d,B\rbrack\) với \(A,B\) lần lượt là các điểm thuộc các nửa mặt phẳng \((P)\) và \((Q)\).
2. Số đo của góc nhị diện
- Số đo của góc phẳng nhị diện \(xOy\) không phụ thuộc vào vị trí của điểm \(O\) trên cạnh nhị diện và được gọi là đó của góc nhị diện đã cho.
- Số đo của góc nhị diện từ \(0^{0}\) đến \(180^{0}\).
Minh họa
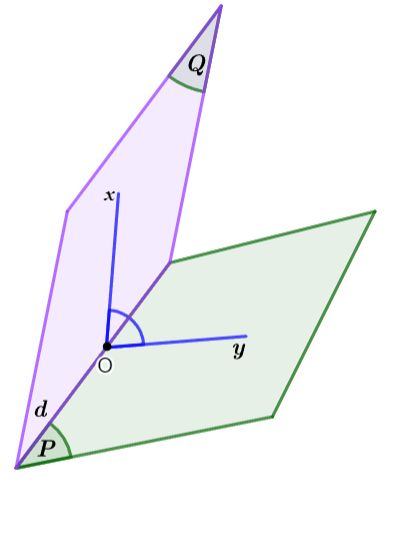
Trong không gian, cho góc nhị diện:
- Một góc có đỉnh thuộc cạnh của góc nhị diện, hai cạnh của góc đó lần lượt thuốc hai mặt phẳng vuông góc với cạnh của góc nhị diện, được gọi là góc phẳng nhị diện của góc nhị diện đã cho.
- Số đo của một góc phẳng nhị diện được gọi là số đo của góc nhị diện đó.
- Nếu số đo góc phẳng nhị diện bằng \(90^{0}\) thì góc nhị diện đó gọi là góc nhị diện vuông.
Ví dụ: Cho hình chóp \(S.ABC\), \(SA\bot(ABC)\), \(AB = AC = a\), \(\widehat{BAC} = 120^{0}\), \(SA = \frac{a\sqrt{3}}{2}\). Tính số đo góc phẳng nhị diện \(\lbrack
S,BC,A\rbrack\)?
Hướng dẫn giải
Hình vẽ minh họa
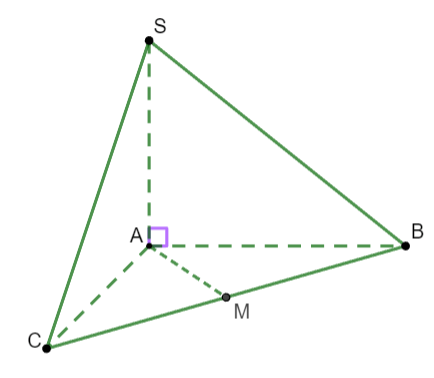
Gọi M là trung điểm của BC
Ta có: \(AB = AC \Rightarrow AM\bot
BC\)
Mặt khác \(SB = SC\) (do \(\Delta SAC = \Delta SAB\)) nên tam giác SBC cân tại S
\(\Rightarrow SM\bot BC\)
\(\Rightarrow \widehat{SMA}\) là góc phẳng nhị diện của \(\lbrack
S,BC,A\rbrack\).
Ta có: \(\widehat{MAB} =
\frac{\widehat{BAC}}{2} = 60^{0}\)
\(\Rightarrow AM = AB.cos\widehat{MAB} =
\frac{a}{2}\)
Trong tam giác \(SAM\) vuông tại \(A\) ta có:
\(\tan\widehat{SAM} = \frac{SA}{MA} =
\frac{a\sqrt{3}}{2}.\frac{2}{a} = \sqrt{3}\)
\(\Rightarrow \widehat{SAM} =
60^{0}\)
