Hai mặt phẳng song song Cánh Diều
Hai mặt phẳng được gọi là song song nếu chúng không có điểm chung.
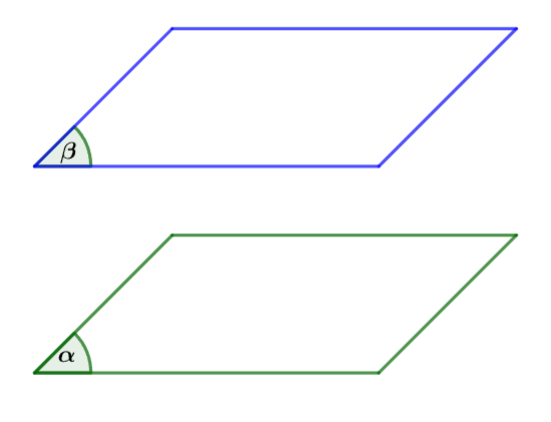
2. Điều kiện và tính chất
Định lí 1 (Dấu hiệu nhận biết hai mặt phẳng song song)
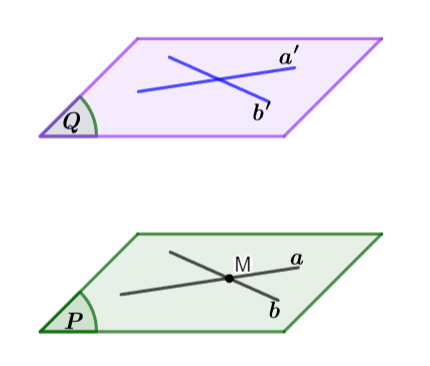
Nếu mặt phẳng 
\((P)\) chứa hai đường thẳng cắt nhau \(a, b\) và \(a, b\) cùng song song với mặt phẳng \((Q)\) thì \((P)\) song song với \((Q)\).
| \(\left\{ \begin{gathered}
a;b \subset \left( P \right) \hfill \\
a \cap b = \left\{ M \right\} \hfill \\
a//\left( Q \right) \hfill \\
b//\left( Q \right) \hfill \\
\end{gathered} \right. \Rightarrow \left( P \right)//\left( Q \right)\) |
 |
Định lí 2 (Tính chất về hai mặt phẳng song song)
Qua một điểm nằm ngoài một mặt phẳng cho trước có một và chỉ một mặt phẳng song song với mặt phẳng đã cho.
Hệ quả 1
Nếu đường thẳng a song song với mặt phẳng \((Q)\) thì có duy nhất một mặt phẳng \((P)\) chứa a và song song với mặt phẳng \((Q)\).
Hệ quả 2
Hai mặt phẳng phân biệt cùng song song với mặt phẳng thứ ba thì song song với nhau.
Định lí 3
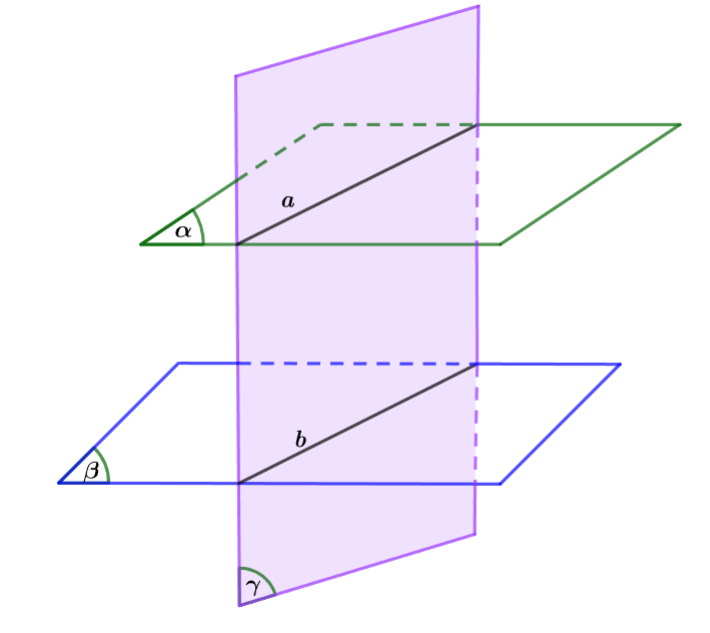
Cho hai mặt phẳng song song \((\alpha)\) và \((β)\). Nếu mặt phẳng \((γ)\) cắt mặt phẳng \((\alpha)\) thì cũng cắt mặt phẳng \((β)\) và hai giao tuyến của chúng song song với nhau.
| \(\left\{ \begin{gathered}
\left( \alpha \right)//\left( \beta \right) \hfill \\
\left( \alpha \right) \cap \left( \gamma \right) = a \hfill \\
\end{gathered} \right. \Rightarrow \left\{ \begin{gathered}
\left( \beta \right) \cap \left( \gamma \right) = b \hfill \\
a//b \hfill \\
\end{gathered} \right.\) |
 |
Ví dụ: Cho hình chóp \(S.ABCD\) có đáy là hình thang có cạnh đáy là \(AB,CD\). Gọi \(M,N\) lần lượt là trung điểm của \(AD;BC\), điểm \(P
\in SA;(P \neq S;P \neq A)\). Xác định giao tuyến của hai mặt phẳng \((SAB);(MNP)\).
Hướng dẫn giải
Hình vẽ minh họa
Ta có: \(\left\{ {\begin{array}{*{20}{l}}
{P = \left( {SAB} \right) \cap \left( {MNP} \right)} \\
{MN \subset \left( {MNP} \right)} \\
{AB \subset \left( {SAB} \right)} \\
{MN//AB}
\end{array}} \right.\)
\(\Rightarrow (SAB) \cap (MNP) =
PQ\) với \(Px//AB//MN,Q \in
SB\).
Vậy giao tuyến của hai mặt phẳng \((SAB);(MNP)\) là đường thẳng qua \(P\) và song song với \(AB\).
3. Định lí Thalès
Định lí 4 (Định lí Thalès)
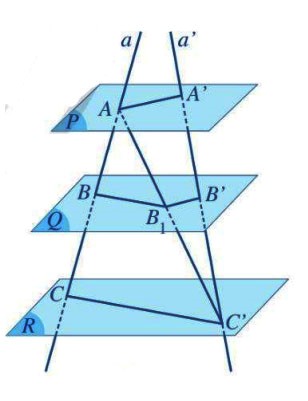
Nếu \(a, b\) là hai cát tuyến bất kì cắt ba mặt phẳng song song \((P), (Q), (R)\) lần lượt tại các điểm \(A, B, C\) và \(A’, B’, C’\) thì \(\frac{AB}{A'B'} = \frac{AC}{A'C'}
= \frac{BC}{B'C'}\).
Ví dụ: Cho tứ diện \(ABCD\). Trên các cạnh \(AD,BC\) theo thứ tự lấy các điểm \(M,N\) sao cho \(AD = 3AM,CB = 3CN\). Giả sử mặt phẳng \((\alpha)\) chứa \(MN\) và song song với \(CD\). Tìm các giao tuyến của tứ diện và mặt phẳng \((\alpha)\). Xác định của hình tạo bởi các giao tuyến này.
Hướng dẫn giải
Hình vẽ minh họa:
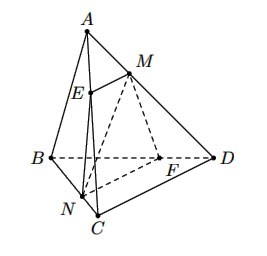
Qua \(M\), kẻ đường thẳng song song với \(CD\) cắt \(AC\) tại \(E\).
Qua \(N\), kẻ đường thẳng song song với \(CD\) cắt \(BD\) tại \(F\).
Khi đó \(ME // NF // CD\) và \((\alpha) \equiv
(MENF)\)
Ta có: \(\left\{ \begin{gathered}
\dfrac{{NF}}{{CD}} = \dfrac{{BN}}{{BC}} = \dfrac{2}{3} \hfill \\
\dfrac{{ME}}{{CD}} = \dfrac{{AM}}{{AD}} = \dfrac{1}{3} \hfill \\
\end{gathered} \right. \Rightarrow NF = 2ME\)
Vậy hình tạo bởi các giao tuyến của tứ diện và mặt phẳng \((\alpha)\) là hình thang \(MENF\) với đáy lớn gấp đôi đáy nhỏ.
