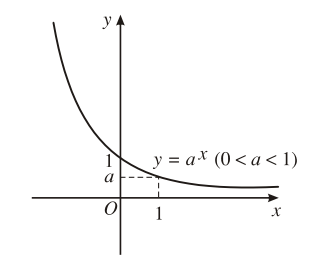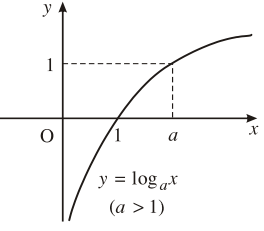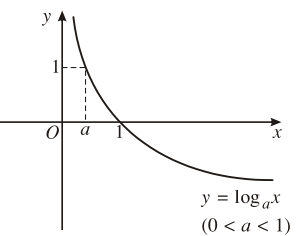Hàm số mũ. Hàm số lôgarit Cánh Diều
1. Định nghĩa
Cho số thực dương ![]() \(a \ne 1\). Hàm số
\(a \ne 1\). Hàm số ![]() \(y=a^x\) được gọi là hàm số mũ cơ số
\(y=a^x\) được gọi là hàm số mũ cơ số ![]() \(a\).
\(a\).
Ví dụ: Tìm tập xác định của hàm số: ![]() \(y = 3^{\dfrac{x - 1}{x + 1}}\)
\(y = 3^{\dfrac{x - 1}{x + 1}}\)
Hướng dẫn giải
Điều kiện xác định của hàm số là ![]() \(x + 1
\neq 0 \Rightarrow x \neq - 1\)
\(x + 1
\neq 0 \Rightarrow x \neq - 1\)
Vậy tập xác định của hàm số là ![]() \(D=\mathbb{R}\backslash\left\{ - 1 \right\}\).
\(D=\mathbb{R}\backslash\left\{ - 1 \right\}\).
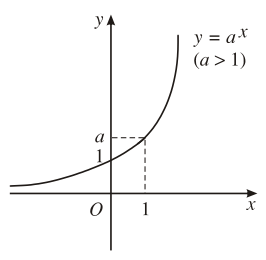
2. Đồ thị và tính chất
|
|
|
|
| 1. Tập xác định |
|
|
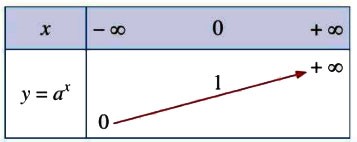
| 2. Sự biến thiên | Đồng biến trên |
Nghịch biến trên |
| 3. Sự liên tục | ||
| 4. Giới hạn đặc biệt |  \(\begin{matrix}
\mathop {\lim }\limits_{x \to - \infty } {a^x} = 0 \hfill \\
\mathop {\lim }\limits_{x \to + \infty } a = + \infty \hfill \\
\end{matrix}\) \(\begin{matrix}
\mathop {\lim }\limits_{x \to - \infty } {a^x} = 0 \hfill \\
\mathop {\lim }\limits_{x \to + \infty } a = + \infty \hfill \\
\end{matrix}\) |
 \(\begin{matrix}
\mathop {\lim }\limits_{x \to - \infty } {a^x} = + \infty \hfill \\
\mathop {\lim }\limits_{x \to + \infty } {a^x} = 0 \hfill \\
\end{matrix}\) \(\begin{matrix}
\mathop {\lim }\limits_{x \to - \infty } {a^x} = + \infty \hfill \\
\mathop {\lim }\limits_{x \to + \infty } {a^x} = 0 \hfill \\
\end{matrix}\) |
| 5. Bảng biến thiên | 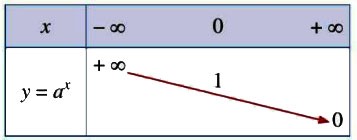 |
 |
|
6. Đồ thị hàm số |
Đồ thị luôn đi qua các điểm |
Đồ thị luôn đi qua các điểm |
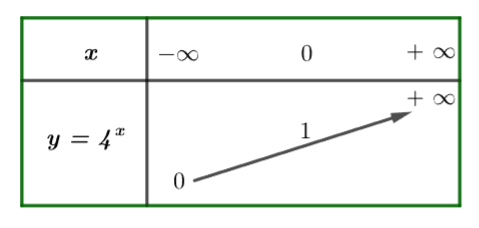
Ví dụ: Lập bảng biến thiên, vẽ đồ thị hàm số: ![]() \(y = 4^{x}\).
\(y = 4^{x}\).
Hướng dẫn giải
Vì hàm số ![]() \(y = 4^{x}\) có cơ số
\(y = 4^{x}\) có cơ số ![]() \(4 > 1\) nên ta có bảng biến thiên như sau:
\(4 > 1\) nên ta có bảng biến thiên như sau:
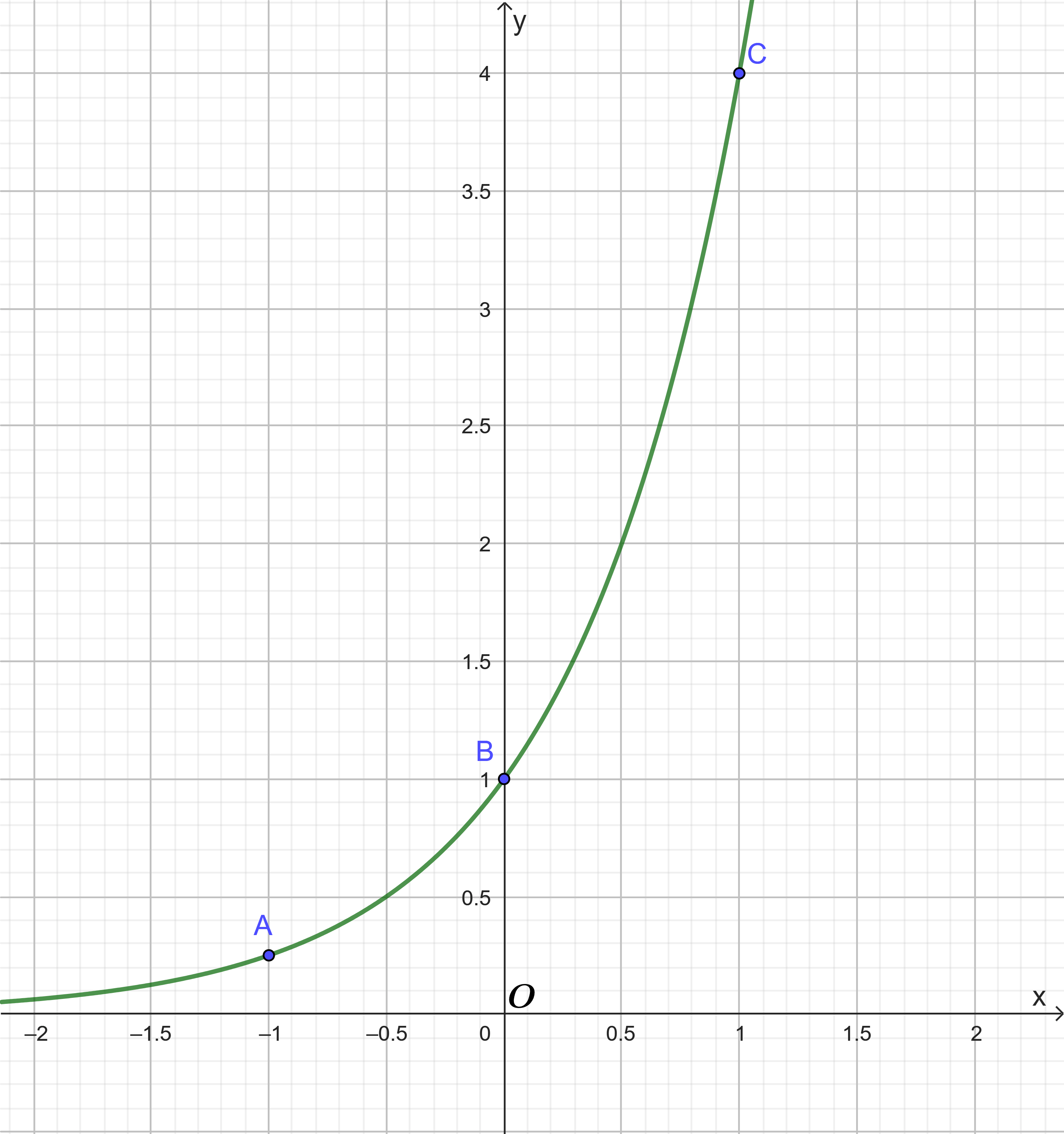
Đồ thị hàm số ![]() \(y = 4^{x}\) là một đường cong nét liền đi qua các điểm
\(y = 4^{x}\) là một đường cong nét liền đi qua các điểm ![]() \(A\left(
- 1;\frac{1}{4} \right),B(0;1),C(1;4)\) như sau:
\(A\left(
- 1;\frac{1}{4} \right),B(0;1),C(1;4)\) như sau:
B. Hàm số lôgari
1. Định nghĩa
Cho ![]() \(a\) là số thực dương và
\(a\) là số thực dương và ![]() \(a \ne 1\). Hàm số
\(a \ne 1\). Hàm số ![]() \(y = \log_{a}x\) được gọi là hàm số lôgarit cơ số
\(y = \log_{a}x\) được gọi là hàm số lôgarit cơ số ![]() \(a\).
\(a\).
Ví dụ: Tìm tập xác định của hàm số:
| a) |
b) |
Hướng dẫn giải
a) Điều kiện xác định của hàm số là
![]() \(4x^{2} - 9 > 0 \Leftrightarrow x^{2}
> \frac{9}{4}\)
\(4x^{2} - 9 > 0 \Leftrightarrow x^{2}
> \frac{9}{4}\)
![]() \(\Leftrightarrow x \in \left( - \infty; -
\frac{3}{2} \right) \cup \left( \frac{3}{2}; + \infty
\right)\)
\(\Leftrightarrow x \in \left( - \infty; -
\frac{3}{2} \right) \cup \left( \frac{3}{2}; + \infty
\right)\)
Vậy tập xác định của hàm số là ![]() \(D = \left(
- \infty; - \frac{3}{2} \right) \cup \left( \frac{3}{2}; + \infty
\right)\)
\(D = \left(
- \infty; - \frac{3}{2} \right) \cup \left( \frac{3}{2}; + \infty
\right)\)
b) Điều kiện xác định của hàm số là
![]() \(x^{2} - 4x + 4 > 0\)
\(x^{2} - 4x + 4 > 0\)
![]() \(\Leftrightarrow (x - 2)^{2} >
0\) luôn đúng với
\(\Leftrightarrow (x - 2)^{2} >
0\) luôn đúng với ![]() \(\forall x \neq
2\)
\(\forall x \neq
2\)
Vậy tập xác định của hàm số là ![]() \(D=\mathbb{R}\backslash\left\{ 2 \right\}\)
\(D=\mathbb{R}\backslash\left\{ 2 \right\}\)
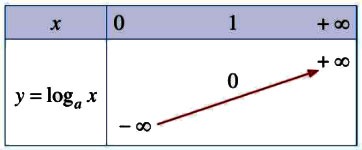
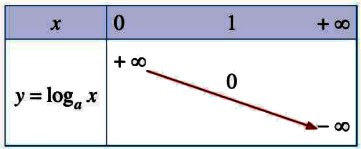
2. Đồ thị và tính chất
|
|
|
|
| 1. Tập xác định |
|
|
| 2. Sự biến thiên | Đồng biến trên |
Nghịch biến trên |
| 3. Sự liên tục | ||
| 4. Giới hạn đặc biệt |
|
|
| 5. Bảng biến thiên |
|
|
|
5. Đồ thị hàm số |
Đi qua các điểm |
Đi qua các điểm |
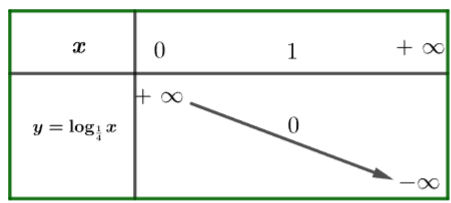
Ví dụ: Lập bảng biến thiên, vẽ đồ thị hàm số: ![]() \(y = \log_{\frac{1}{4}}x\).
\(y = \log_{\frac{1}{4}}x\).
Hướng dẫn giải
Vì hàm số ![]() \(y = \log_{\frac{1}{4}}x\) có cơ số
\(y = \log_{\frac{1}{4}}x\) có cơ số ![]() \(\frac{1}{4} < 1\) nên ta có bảng biến thiên như sau:
\(\frac{1}{4} < 1\) nên ta có bảng biến thiên như sau:
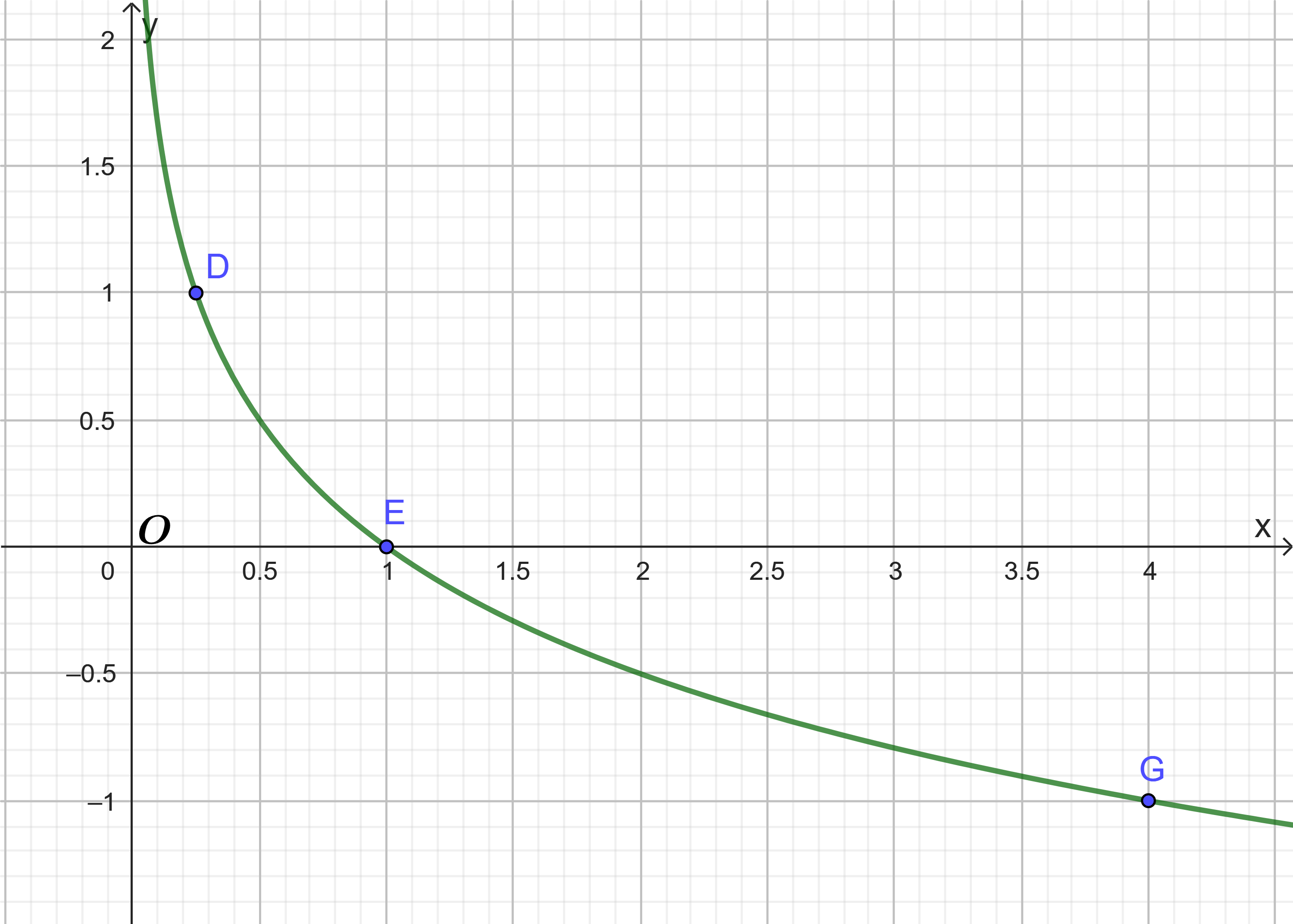
Đồ thị hàm số ![]() \(y = \log_{\frac{1}{4}}x\) là một đường cong liền nét đi qua các điểm
\(y = \log_{\frac{1}{4}}x\) là một đường cong liền nét đi qua các điểm ![]() \(D\left(
\frac{1}{4};1 \right),E(1;0),G(4; - 1)\) như sau:
\(D\left(
\frac{1}{4};1 \right),E(1;0),G(4; - 1)\) như sau:
Ví dụ: Tìm tất cả các giá trị của tham số m để hàm số ![]() \(y = \log_{m^{2} - 2m + 1}x\) nghịch biến trên khoảng
\(y = \log_{m^{2} - 2m + 1}x\) nghịch biến trên khoảng ![]() \((0; + \infty)\).
\((0; + \infty)\).
Hướng dẫn giải
Hàm số ![]() \(y = \log_{m^{2} - 2m + 1}x\) nghịch biến trên khoảng
\(y = \log_{m^{2} - 2m + 1}x\) nghịch biến trên khoảng ![]() \((0; +
\infty)\) khi và chỉ khi
\((0; +
\infty)\) khi và chỉ khi
![]() \(0 < m^{2} - 2m + 1 <
1\)
\(0 < m^{2} - 2m + 1 <
1\)
![]() \(\Leftrightarrow \left\{ \begin{matrix}
0 < m < 2 \\
m \neq 1 \\
\end{matrix} \right.\)
\(\Leftrightarrow \left\{ \begin{matrix}
0 < m < 2 \\
m \neq 1 \\
\end{matrix} \right.\)