Hàm số lượng giác và đồ thị Cánh Diều
a) Hàm số chẵn, hàm số lẻ
Cho hàm số 
\(y=f(x)\) có tập xác định \(D\).
- Hàm số \(f\left( x \right)\) được gọi là hàm số chẵn nếu \(\forall x \in D\) thì \(\left\{ \begin{gathered}
- x \in D \hfill \\
f\left( { - x} \right) = f\left( x \right) \hfill \\
\end{gathered} \right.\)
- Hàm số \(f\left( x \right)\) được gọi là hàm số lẻ nếu \(\forall x \in D\) thì \(\left\{ \begin{gathered}
- x \in D \hfill \\
f\left( { - x} \right) = - f\left( x \right) \hfill \\
\end{gathered} \right.\)
Chú ý:
- Đồ thị của một hàm số chẵn nhận trục tung làm trục đối xứng.
- Đồ thị của một hàm số lẻ nhận trục hoành làm trục đối xứng.
b) Hàm số tuần hoàn
Định nghĩa: Hàm số có tập xác định được gọi là hàm số tuần hoàn, nếu tồn tại một số \(T \ne 0\) sao cho với mọi \(x \in D\) ta có:
- \(\left\{ {\begin{array}{*{20}{c}}
{x - T \in D} \\
{x + T \in D}
\end{array}} \right.\)
- \(f\left( {x + T} \right) = f\left( x \right)\)
Chú ý: Cho hàm số tuần hoàn chu kì \(T\). Từ đồ thị hàm số đó trên đoạn \([a; a + T]\), ta dịch chuyển song song với trục hoành sang phải (hoặc sang trái) theo đoạn có độ dài T thì được đồ thị hàm số trên đoạn \([a + T; a + 2T]\) (hoặc \([a - T; a]\)).
2. Hàm số y = sinx
a) Định nghĩa
- Quy tắc đặt tương ứng với mỗi số thực \(x\) với số thực \(\sin x\) được gọi là hàm số sin, kí hiệu là \(y = \sin x\).
- Tập xác định của hàm số sin là \(\mathbb{R}\).
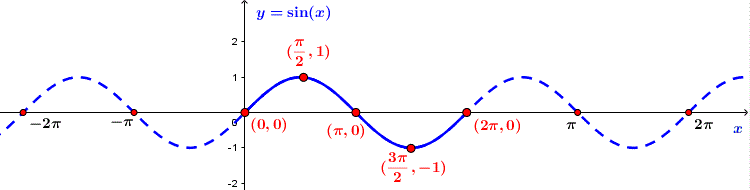
b) Đồ thị hàm số và tính chất
Hàm số \(y = \sin x\)
- Tập xác định: \(D = \mathbb{R}\)
- Tập giá trị [-1; 1] hay \(- 1 \leqslant \operatorname{sinx} \leqslant 1,\forall x \in \mathbb{R}\)
- Hàm số là hàm số lẻ tuần hoàn với chu kì \(T = 2\pi\)
- Đồng biến trên mỗi khoảng \(\left( { - \frac{\pi }{2} + k2\pi ;\frac{\pi }{2} + k2\pi } \right)\) và nghịch biến trên mỗi khoảng \(\left( {\frac{\pi }{2} + k2\pi ;\frac{{3\pi }}{2} + k2\pi } \right)\), \(k \in \mathbb{Z}\)
- Có đồ thị đối xứng qua gốc tọa độ và gọi là một đường hình sin.
Đồ thị hàm số \(y = \sin x\)
Ví dụ: Xét tính chẵn lẻ của hàm số \(y = 2x\sin x\).
Hướng dẫn giải
Tập xác định \(D = \mathbb{R}\) là tập đối xứng do đó \(\forall x \in D \Rightarrow - x \in D\left( * \right)\)
Đặt \(y = f\left( x \right) = 2x.\sin x\)
Với \(\forall x \in D\) ta có:
\(f\left( { - x} \right) = 2\left( { - x} \right).\sin \left( { - x} \right) = 2x.\sin x = f\left( x \right)\left( {**} \right)\)
Từ (*) và (**) suy ra hàm số đã cho là hàm số chẵn.
3. Hàm số y = cosx
a) Định nghĩa
- Quy tắc đặt tương ứng với mỗi số thực \(x\) với số thực \(\cos x\) được gọi là hàm số cosin, kí hiệu là \(y = \cos x\).
- Tập xác định của hàm số cos là \(\mathbb{R}\).
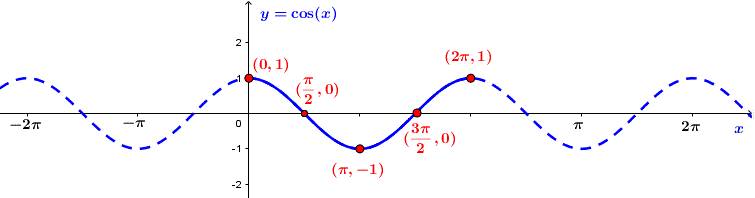
b) Đồ thị hàm số và tính chất
Hàm số \(y = \cos x\)
- Tập xác định: \(D = \mathbb{R}\)
- Tập giá trị [-1; 1] hay \(- 1 \leqslant \operatorname{cosx} \leqslant 1,\forall x \in \mathbb{R}\)
- Hàm số là hàm chẵn tuần hoàn với chu kì \(T = 2\pi\)
- Đồng biến trên mỗi khoảng \(\left( { - \pi + k2\pi ;k2\pi } \right)\) và nghịch biến trên mỗi khoảng \(\left( {k2\pi ;\pi + k2\pi } \right)\), \(k \in \mathbb{Z}\)
- Có đồ thị là một đường hình sin đối xứng qua trục tung.
Đồ thị hàm số \(y = \cos x\)
Ví dụ: Xét tính chẵn lẻ của hàm số \(y = f(x) = \frac{\cos x + x^{2} -1}{\sin^{4}x}\)
Hướng dẫn giải
Tập xác định của hàm số là \(D = \mathbb{R}\setminus \{ k\pi,k \in \mathbb{Z}\}\)
\(\forall x \in D \Rightarrow - x \in
D\)
\(f( - x) = \frac{\cos( - x) + ( - x)^{2} -1}{\sin^{4}( - x)}\)\(= \frac{cosx + x^{2} - 1}{\sin^{4}x} =
f(x),\forall x \in D\)
Vậy hàm số đã cho là hàm số chẵn.
4. Hàm số y = tanx
a) Định nghĩa
Hàm số được cho bằng công thức \(y = \frac{{\sin x}}{{\cos x}}\) được gọi là hàm số tang, kí hiệu là \(y = \tan x\).
Tập xác định của hàm số tang là \(\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi |k \in \mathbb{Z}} \right\}\).
Ví dụ: Tìm tập xác định của hàm số \(y =
\tan\left( 2x + \frac{\pi}{6} \right)\)
Hướng dẫn giải
Xét \(\cos\left( 2x + \frac{\pi}{6} \right)
\neq 0\)
\(\Rightarrow 2x + \frac{\pi}{6} \neq
\frac{\pi}{2} + k\pi\)
\(\Rightarrow x \neq \frac{\pi}{6} +
\frac{k\pi}{2},\left( k\mathbb{\in Z} \right)\)
Vậy tập xác định của hàm số đã cho là \(D =
\left\{ \mathbb{R}\backslash\frac{\pi}{6} + \frac{k\pi}{2},\left(
k\mathbb{\in Z} \right) \right\}\)
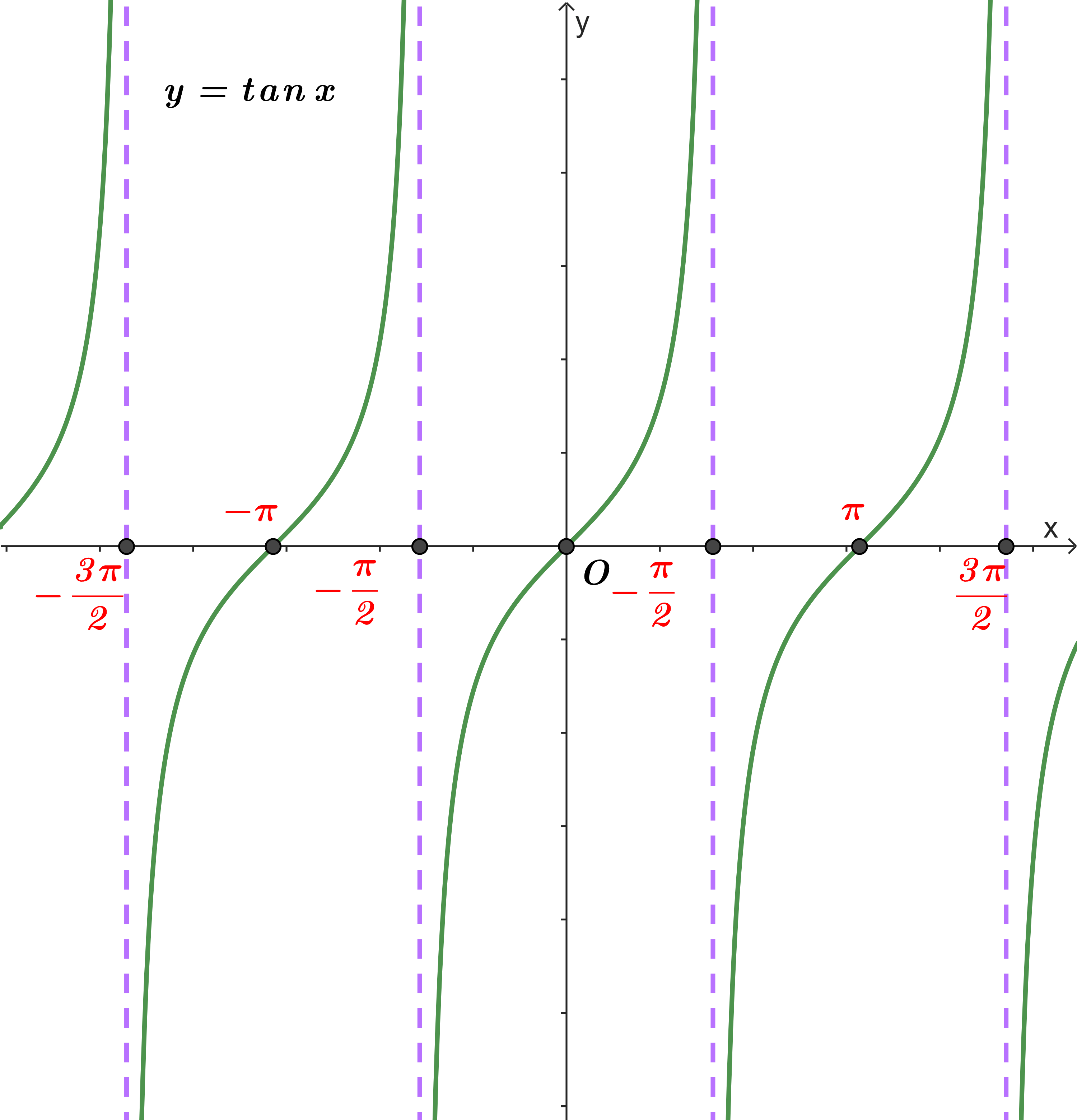
b) Đồ thị hàm số và tính chất
Hàm số \(y = \tan x\)
- Tập xác định: \(D = \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right\}\)
- Tập giá trị: \(\mathbb{R}\)
- Hàm số là hàm lẻ tuần hoàn với chu kì \(T = \pi\)
- Đồng biến trên mỗi khoảng \(\left( { - \frac{\pi }{2} + k\pi ;\frac{\pi }{2} + k\pi } \right)\)
- Có đồ thị đối xứng qua gốc tọa độ.
Đồ thị hàm số \(y = \tan x\)
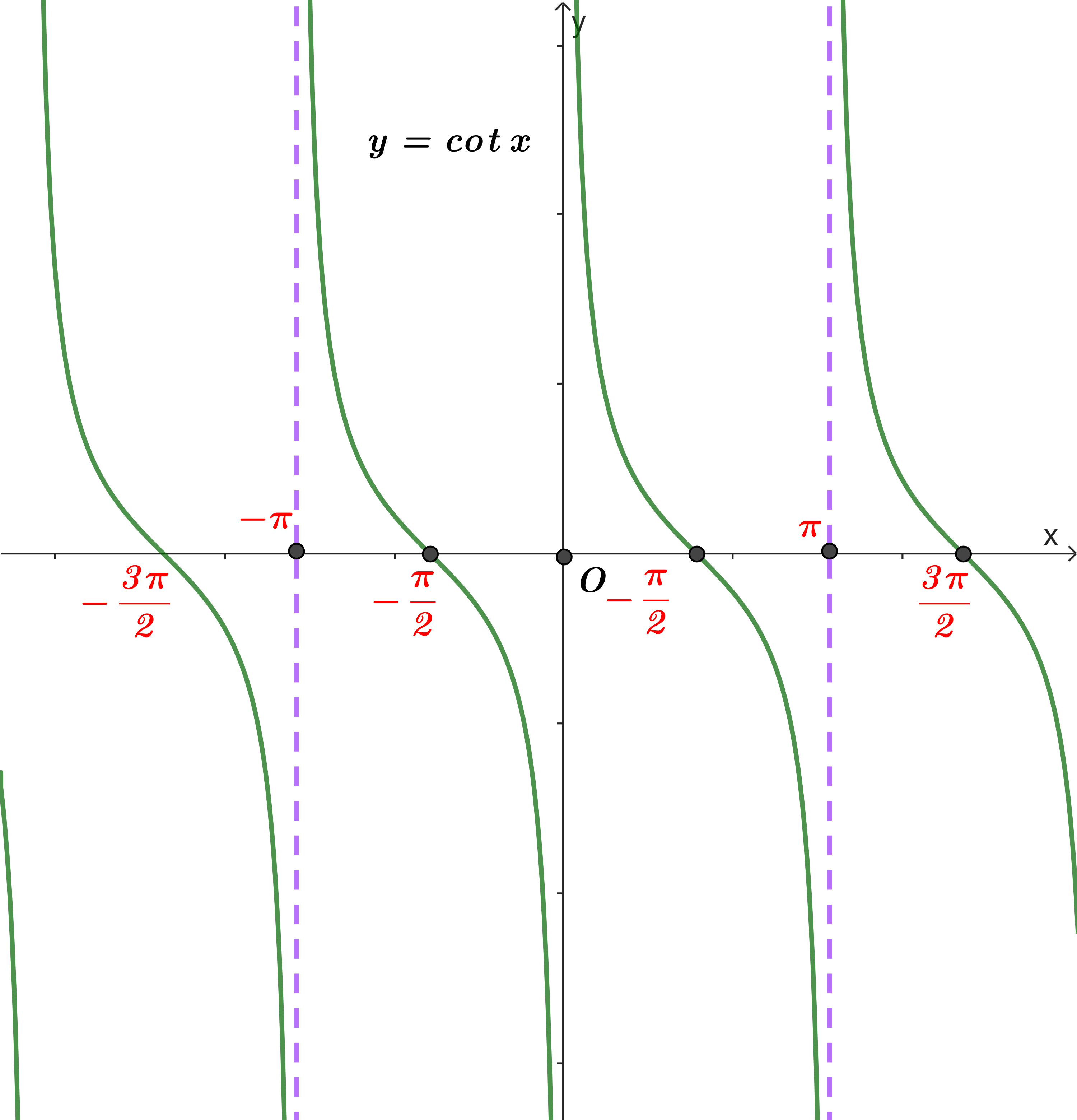
5. Hàm số y = cotx
a) Định nghĩa
Hàm số được cho bằng công thức \(y = \frac{{\cos x}}{{\sin x}}\) được gọi là hàm số cotang, kí hiệu là \(y = \cot x\).
Tập xác định của hàm số cotang là \(\mathbb{R}\backslash \left\{ {k\pi |k \in \mathbb{Z}} \right\}\).
Ví dụ: Tìm tập xác định của hàm số \(y =
\cot\left( - 2x - \frac{\pi}{3} \right)\)
Hướng dẫn giải
Xét \(\sin\left( - 2x - \frac{\pi}{3}
\right) \neq 0\)
\(\Rightarrow - 2x - \frac{\pi}{3} \neq
k\pi\)
\(\Rightarrow x \neq - \frac{\pi}{6} -\frac{k\pi}{2};\left( k\in\mathbb{ Z} \right)\)
Vậy tập xác định của hàm số đã cho là \(D =\left\{ \mathbb{R}\backslash - \frac{\pi}{6} - \frac{k\pi}{2},\left(k\in\mathbb{ Z} \right) \right\}\)
b) Đồ thị hàm số và tính chất
Hàm số \(y = \cot x\)
- Tập xác định: \(D = \mathbb{R}\backslash \left\{ {k\pi ,k \in \mathbb{Z}} \right\}\)
- Tập giá trị: \(\mathbb{R}\)
- Hàm số là hàm lẻ tuần hoàn với chu kì \(T = \pi\)
- Nghịch biến trên mỗi khoảng \(\left( {k\pi ;\pi + k\pi } \right),k \in \mathbb{Z}\)
- Có đồ thị đối xứng qua gốc tọa độ.
Đồ thị hàm số \(y = \cot x\)
