Góc lượng giác. Giá trị lượng giác của góc lượng giác
1. Góc hình học và số đo của chúng
- Góc hình học là hình gồm hai tia chung gốc.
- Mỗi góc có một số đo, đơn vị đo góc là độ.
- Nếu chia đường tròn thành 360 cung tròn bằng nhau thì góc ở tâm chắn mỗi cung 10.
- Số đo của một góc hình học không vượt quá 1800.
- Nếu trên đường tròn ta lấy một cung tròn có độ dài bằng bán kính thì góc ở tâm chắn cung đó gọi là góc có số đo 1 radian (hay rad).
Chú ý:
 \(1rad = {\left( {\frac{{180}}{\pi }} \right)^0}\) |
\({1^0} = {\left( {\frac{\pi }{{180}}} \right)^0}\) |
Ví dụ: Hoàn thành bảng chuyển đổi số đo góc sau:
|
Độ |
2600 |
? |
1400 |
? |
|
Radian |
? |
\(\frac{{5\pi }}{9}\) |
? |
\(\frac{{7\pi }}{4}\) |
Hướng dẫn giải
|
Độ |
2600 |
1000 |
1400 |
3150 |
|
Radian |
\(\frac{{13\pi }}{9}\) |
\(\frac{{5\pi }}{9}\) |
\(\frac{{7\pi }}{9}\) |
\(\frac{{7\pi }}{4}\) |
Ví dụ: Một đường tròn có bán kính 20cm. Tìm độ dài của các cung trên đường tròn đó có số đo sau:
|
a) |
b) |
Hướng dẫn giải
a) Độ dài cung đường tròn là: \(l = \frac{\pi }{{12}}.20 \approx 5,236\left( {cm} \right)\)
b) Ta có: \({35^0} = \frac{{7\pi }}{{36}}\)
Độ dài cung đường tròn là: \(l = \frac{{7\pi }}{{36}}.20 \approx 12,22\left( {cm} \right)\)
2. Góc lượng giác và số đo của chúng
a) Khái niệm
Cho hai tia \(Ou, Ov\).
Nếu tia Om quay chỉ theo chiều dương (hay chỉ theo chiều âm) xuất phát từ tia Ou đến trùng với tia Ov thì ta nói: Tia Om quét một góc lượng giác với tia đầu Ou và tia cuối Ov. Kí hiệu: \((Ou, Ov)\).
Minh họa
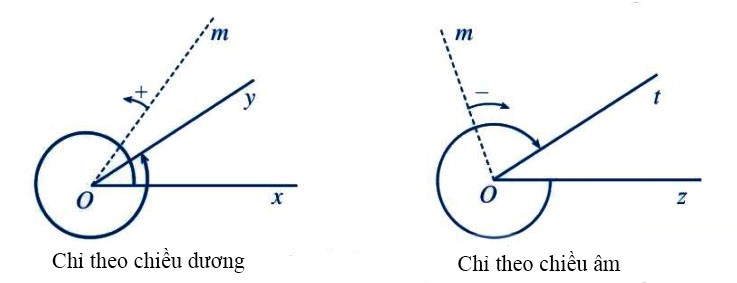
Chú ý:
- Khi tia Om quay góc a0 thì góc lượng giác mà tia đó quét được có số đo a0, (tương tự với rad).
- Nếu góc lượng giác \((Ou, Ov)\) có số đo a0 thì ta kí hiệu \(sđ(Ou, Ov) = a\) hoặc \((Ou, Ov) = a\).
- Mỗi một góc lượng giác gốc O xác định bởi tia đầu Ou và tia cuối Ov và số đo của góc đó.
Minh họa:
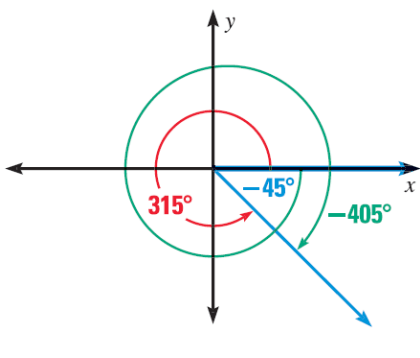
b) Tính chất
Cho hai góc lượng giác \((Ou, Ov); (O’u’, O’v’)\) có tia đầu trùng nhau \((Ou ≡ O’u’)\) tia cuối trùng nhau \((Ov≡ O’v’)\). Khi đó
- Nếu sử dụng đơn vị đo là độ thì ta nói:
\(\left( {Ou,Ov} \right) = \left( {O'u',O'v'} \right) + k{.360^0},\left( {k \in \mathbb{Z}} \right)\)
- Nếu sử dụng đơn vị đo là radian thì công thức trên có thể viết như sau:
\(\left( {Ou,Ov} \right) = \left( {O'u',O'v'} \right) + k2\pi ,\left( {k \in \mathbb{Z}} \right)\)
Với ba tia \(Ou,Ov,Ow\) tùy ý ta có:
\(\left( {Ou,Ov} \right) + \left( {Ov,Ow} \right) = \left( {Ou,Ow} \right) + k2\pi ,\left( {k \in \mathbb{Z}} \right)\)
Ví dụ: Cho góc lượng giác (Ou, Ov) có số đo \(\frac{\pi }{5}\). Hỏi trong các góc \(\frac{{6\pi }}{5};\frac{{9\pi }}{5};\frac{{ - 11\pi }}{5};\frac{{31\pi }}{5};\frac{{ - 14\pi }}{5}\) những góc nào có số đo của một góc lượng giác có cùng tia đầu, tia cuối với góc đã cho?
Hướng dẫn giải
Ta có:
\(\begin{matrix}
\dfrac{{6\pi }}{5} = \pi + \dfrac{\pi }{5} \hfill \\
\dfrac{{9\pi }}{5} = 2\pi - \dfrac{\pi }{5} \hfill \\
\end{matrix}\)
\(\begin{matrix}
\dfrac{{ - 11\pi }}{5} = - 2\pi - \dfrac{\pi }{5} \hfill \\
\dfrac{{31\pi }}{5} = 6\pi + \dfrac{\pi }{5} \hfill \\
\dfrac{{ - 14\pi }}{5} = - 3\pi + \dfrac{\pi }{5} \hfill \\
\end{matrix}\)
Nhận thấy số đo của một góc lượng giác có tia đầu và tia cuối với góc đã cho khi ta quay góc đó chẵn 1 vòng mà 1 vòng có số đo \(2\pi\)
Suy ra những góc thỏa mãn yêu cầu đề bài là \(\frac{{9\pi }}{5};\frac{{ - 11\pi }}{5};\frac{{31\pi }}{5}\).
B. Giá trị lượng giác của góc lượng giác
1. Đường tròn lượng giác
Trong mặt phẳng tọa độ đã được định hướng Oxy, lấy điểm A(1; 0). Đường tròn tâm O bán kính OA = 1 được gọi là đường tròn lượng giác (hay đường tròn đơn vị) gốc A.
+ Chiều dương ngược chiều kim đồng hồ.
+ Chiều âm cùng chiều kim đồng hồ.
Minh họa
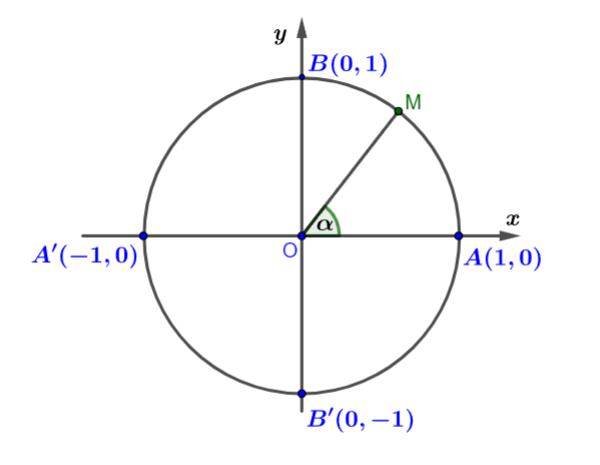
Ví dụ: Xác định điểm P trên đường tròn lượng giác sao cho \(\left( {OA;OP} \right) = \frac{{5\pi }}{4}\).
Hướng dẫn giải
Gọi điểm M là điểm chính giữa của cung A’B’ trên đường tròn lượng giác.
Ta có: \(\left( {OA;OP} \right) = \frac{{5\pi }}{4}\) được biểu diễn như hình vẽ sau:
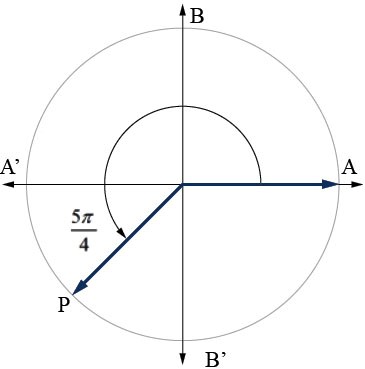
2. Giá trị lượng giác của góc lượng giác
a) Định nghĩa
Giả sử điểm \(M\left( {x;y} \right)\) là điểm trên đường tròn lượng giác, biểu diễn góc lượng giác có số đo \(\alpha\) (như hình vẽ):
- Hoành độ \(x = \cos \alpha\)
- Tung độ \(y = \sin \alpha\)
- \(\tan \alpha = \frac{y}{x} = \frac{{\sin \alpha }}{{\cos \alpha }};\left( {x \ne 0} \right)\) hay \(\tan \alpha\) xác định khi \(\alpha \ne \frac{\pi }{2} + k\pi ;\left( {k \in \mathbb{Z}} \right)\)
- \(\cot \alpha = \frac{x}{y} = \frac{{\cos \alpha }}{{\sin \alpha }};\left( {y \ne 0} \right)\) hay \(\cot \alpha\) xác định khi \(\alpha \ne k\pi ;\left( {k \in \mathbb{Z}} \right)\)
b) Dấu các giá trị lượng giác của góc lượng giác
Dấu của các giá trị lượng giác của một góc lượng giác phụ thuộc vào vị trí điểm biểu diễn M trên đường tròn lượng giác.
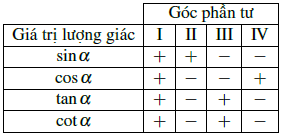
Ví dụ: Xét dấu các giá trị lượng giác \(\alpha = \frac{{5\pi }}{6}\).
Hướng dẫn giải
Giả sử điểm M trên đường tròn lượng giác sao cho \(\alpha = \frac{{5\pi }}{6}\)
Do \(\frac{\pi }{2} < \frac{{5\pi }}{6} < \pi\) nên điểm M thuộc góc phần tư thứ II.
Do đó \(\left\{ \begin{gathered}
\sin \left( {\frac{{5\pi }}{6}} \right) > 0;\cos \left( {\frac{{5\pi }}{6}} \right) < 0 \hfill \\
\tan \left( {\frac{{5\pi }}{6}} \right) < 0;\cot \left( {\frac{{5\pi }}{6}} \right) < 0 \hfill \\
\end{gathered} \right.\)
3. Công thức lượng giác cơ bản
| \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\) |
\(1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }};\left( {\alpha \ne \frac{\pi }{2} + k\pi ;k \in \mathbb{Z}} \right)\) |
| \(1 + {\cot ^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }};\left( {\alpha \ne k\pi ;k \in \mathbb{Z}} \right)\) |
\(\tan \alpha .\cot \alpha = 1;\left( {\alpha \ne \frac{{k\pi }}{2};k \in \mathbb{Z}} \right)\) |
Ví dụ: Rút gọn biểu thức: \(A = \tan x + \frac{{\cos x}}{{1 + \sin x}}\)
Hướng dẫn giải
Ta có:
\(A = \tan x + \frac{{\cos x}}{{1 + \sin x}} = \frac{{\sin x}}{{\cos x}} + \frac{{\cos x}}{{1 + \sin x}}\)
\(= \frac{{\sin x\left( {1 + \sin x} \right) + {{\cos }^2}x}}{{\cos x\left( {1 + \sin x} \right)}} = \frac{{\sin x + {{\sin }^2}x + {{\cos }^2}x}}{{\cos x\left( {1 + \sin x} \right)}}\)
\(= \frac{{\sin x + 1}}{{\cos x\left( {1 + \sin x} \right)}} = \frac{1}{{\cos x}}\)
4. Bảng giá trị lượng giác của một số góc đặc biệt
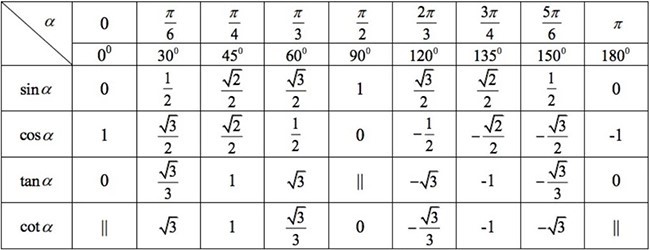
Ví dụ: Tính giá trị biểu thức: \(A = {\tan ^2}\frac{\pi }{3} + {\sin ^2}\frac{\pi }{4} + \cot \frac{\pi }{4} + \cos \frac{\pi }{2}\)
Hướng dẫn giải
Ta có:
\(\begin{matrix}
A = {\tan ^2}\dfrac{\pi }{3} + {\sin ^2}\dfrac{\pi }{4} + \cot \dfrac{\pi }{4} + \cos \dfrac{\pi }{2} \hfill \\
= {\left( {\sqrt 3 } \right)^2} + {\left( {\dfrac{{\sqrt 2 }}{2}} \right)^2} + 1 + 0 = 3 + \dfrac{1}{2} + 1 = \dfrac{9}{2} \hfill \\
\end{matrix}\)
5. Giá trị lượng giác của các góc có liên quan đặc biệt
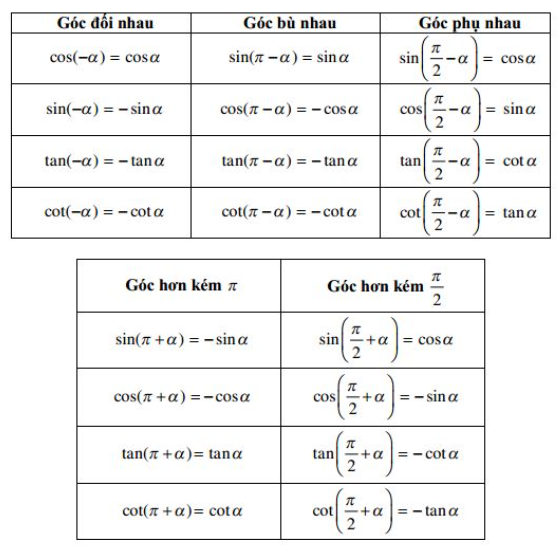
Ví dụ: Rút gọn các biểu thức sau:
a) \(M = \cos \left( {a + \frac{\pi }{2}} \right) + \cos \left( {2\pi - a} \right) + \cos \left( {3\pi + a} \right)\)
b) \(N = \cos \left( {5\pi - x} \right) - \sin \left( {\frac{{3\pi }}{2} + x} \right) + \tan \left( {\frac{{3\pi }}{2} - x} \right) + \cos \left( {3\pi - x} \right)\)
Hướng dẫn giải
a) \(M = \cos \left( {a + \frac{\pi }{2}} \right) + \cos \left( {2\pi - a} \right) + \cos \left( {3\pi + a} \right)\)
\(\begin{matrix}
M = - \sin x + \cos \left( { - x} \right) - \cos x \hfill \\
M = - \sin x + \cos x - \cos x \hfill \\
M = - \sin x \hfill \\
\end{matrix}\)
b) \(N = \cos \left( {5\pi - x} \right) - \sin \left( {\frac{{3\pi }}{2} + x} \right) + \tan \left( {\frac{{3\pi }}{2} - x} \right) + \cos \left( {3\pi - x} \right)\)
\(N = \cos \left( {4\pi + \pi - x} \right) - \sin \left( {\pi + \frac{\pi }{2} + x} \right) + \tan \left( {\pi + \frac{\pi }{2} - x} \right) + \cot \left( {2\pi + \pi - x} \right)\)
\(N = \cos \left( {\pi - x} \right) + \sin \left( { + \frac{\pi }{2} + x} \right) + \tan \left( {\frac{\pi }{2} - x} \right) + \cot \left( {\pi - x} \right)\)
\(N = - \cos x + \cos x + \cot x + - \cot x = 0\)
