13 đề thi Toán 7 học kì 1 Kết nối tri thức

Bộ 13 đề thi học kì 1 môn Toán 7 được biên soạn sát với chương trình sách giáo khoa Kết nối tri thức với cuộc sống cung cấp đầy đủ đáp án và lời giải chi tiết cho từng đề thi, cho phép học sinh không chỉ làm bài mà còn tự kiểm tra, đánh giá chính xác năng lực bản thân, nhận diện được những phần kiến thức còn yếu để kịp thời củng cố trước kỳ thi.

Đối với quý Thầy Cô, bộ đề này là một nguồn tham khảo quý giá, giúp tiết kiệm thời gian trong việc xây dựng, điều chỉnh và ra đề kiểm tra chất lượng.

Lưu ý: Dưới đây là trích dẫn một số đề thi trong bộ đề. Toàn bộ 13 đề và đáp án có trong file tải về. Mời các bạn tải về xem trọn bộ tài liệu

Đề thi Toán 7 học kì 1 Kết nối tri thức

Đề thi

PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)

Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây:

Câu 1. Trong các câu sau, câu nào đúng?

A. Số hữu tỉ âm nhỏ hơn số hữu tỉ dương;

B. Số 0 là số hữu tỉ dương;

C.Số nguyên âm không phải là số hữu tỉ âm;

D. Tập hợp Q gồm các số hữu tỉ dương và các số hữu tỉ âm.

Câu 2. Trong các số sau, số nào biểu diễn số đối của số hữu tỉ –0,5?

A. 1/2;

B. −1/2;

C. 2;

D. –2.

Câu 3. Số \(-\frac{1}{3}\) là số:

A. Số thập phân vô hạn không tuần hoàn;

B. Số thập phân hữu hạn;

C. Số thập phân vô hạn tuần hoàn;

D. Số vô tỉ.

Câu 4. \(\sqrt{64}\) bằng:

A. ± 8;

B. –8;

C. 8;

D. 64.

Câu 5. Nếu |x| = 2 thì:

A. x = 2;

B. x = –2;

C. x = 2 hoặc x = –2;

D. Không có giá trị nào của x thỏa mãn.

Câu 6. Quan sát hình vẽ.

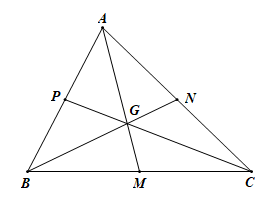
Có tất cả bao nhiêu góc kề bù với \(\hat{NGC}\)?

A. 1;

B. 2;

C. 3;

D. 4.

Câu 7. Trong các câu sau, câu nào không phải định lí?

A. Nếu hai góc bằng nhau thì chúng đối đỉnh;

B. Nếu hai góc kề bù thì tổng số đo của chúng bằng 180°;

C. Nếu hai góc bù nhau thì tổng số đo của chúng bằng 180°;

D. Nếu hai góc đối đỉnh thì chúng bằng nhau.

Câu 8. Tổng số đo ba góc của một tam giác là

A. 45°;

B. 60°;

C. 90°;

D. 180°.

Câu 9. Phát biểu nào dưới đây là sai?

A. Hai tam giác có các góc tương ứng bằng nhau là hai tam giác bằng nhau;

B. Hai tam giác bằng nhau thì có các góc tương ứng bằng nhau;

C. Hai tam giác có các góc tương ứng bằng nhau, các cạnh tương ứng bằng nhau thì hai tam giác đó bằng nhau.

D. Hai tam giác bằng nhau là hai tam giác có các cạnh bằng nhau và có các góc bằng nhau.

Câu 10. Cho các hình vẽ sau:

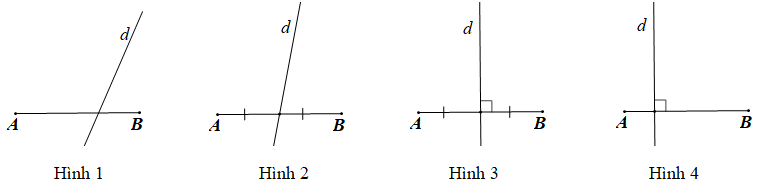
Hình vẽ nào minh họa đường thẳng d là đường trung trực của đoạn thẳng AB?

A. Hình 1;

B. Hình 2;

C. Hình 3;

D. Hình 4.

Câu 11. Thân nhiệt (°C) của bạn An trong cùng khung giờ 7h sáng các ngày trong tuần được ghi lại trong bảng sau:

Bạn An đã thu được dữ liệu trên bằng cách nào?

A. Xem tivi;

B. Lập bảng hỏi;

C. Ghi chép số liệu thống kê hằng ngày;

D. Thu thập từ các nguồn có sẵn như: sách, báo, web.

Câu 12. Kết quả tìm hiểu về khả năng chơi cầu lông của các bạn học sinh nam lớp 7C cho bởi bảng thống kê sau:

Kết quả tìm hiểu về khả năng chơi bóng đá của các bạn học sinh nữ của lớp 7C được cho bởi bảng thống kê sau:

Khẳng định nào dưới đây là đúng?

A. Dữ liệu về khả năng chơi cầu lông của các bạn học sinh nam lớp 7C đại diện cho khả năng chơi cầu lông học sinh cả lớp 7C;

B. Dữ liệu về khả năng chơi bóng đá của các bạn học sinh nữ lớp 7C đại diện cho khả năng chơi cầu lông học sinh cả lớp 7C;

C. Dữ liệu về khả năng chơi cầu lông và bóng đá được thống kê chưa đủ đại diện cho khả năng chơi thể thao của các bạn lớp 7C;

D. Lớp 7C có 35 học sinh.

Phần II. Tự luận (7 điểm):

Bài 1: (2,0 điểm )

Thực hiện phép tính:

a) \(\left( { - \dfrac{3}{4} + \dfrac{2}{3}} \right):\dfrac{5}{{11}} + \left( { - \dfrac{1}{4} + \dfrac{1}{3}} \right):\dfrac{5}{{11}}\)

b) \(\dfrac{{{{27}^{10}}{{.16}^{25}}}}{{{6^{30}}{{.32}^{15}}}}\)

c) \(\left| {\dfrac{3}{5} - \dfrac{1}{{10}}} \right| - \sqrt {\dfrac{{36}}{{25}}} + {\left( {\dfrac{3}{{10}}} \right)^5}:{\left( {\dfrac{3}{{10}}} \right)^4}\)

d) \(\sqrt {144} + \sqrt {49} - 10\sqrt {\dfrac{4}{{25}}}\)

Bài 2: (2,0 điểm)

Tìm x, biết:

a) \(\left( { - \dfrac{1}{2}} \right) + \left( {\dfrac{4}{5} + x} \right) = 1\dfrac{1}{2}\)

b) \({\left( {x - \dfrac{1}{3}} \right)^2} = \dfrac{1}{9}\)

c) \(5.\sqrt x - \sqrt {\dfrac{1}{{25}}} = 0\)

d) \(\left| {0,3 - x} \right| = \dfrac{1}{3}\)

Bài 3: (1,0 điểm)

Tính số đo của góc x trong hình vẽ dưới đây:

Bài 4: (1,5 điểm)

Cho tam giác ABC cân tại A có \(\widehat {A{\rm{ }}} = 120^\circ\). Trên cạnh BC lấy hai điểm M, N sao cho MA, NA lần lượt vuông góc với AB, AC. Chứng minh rằng:

a) \(\Delta BAM = \Delta CAN\);

b) Các tam giác ANB, AMC lần lượt cân tại N, M.

Bài 5: (0,5 điểm)

Tìm số thực x, biết: \(\left| x \right| + \left| {x + 2} \right| = 0\).

******************