Top 12 đề thi học kì 1 Toán 7 Cánh diều
Đây là tài liệu Cao cấp - Chỉ dành cho Thành viên VnDoc ProPlus.
- Tải tất cả tài liệu lớp 7 (Trừ Giáo án, bài giảng)
- Trắc nghiệm không giới hạn
Bộ Đề Thi Học Kì 1 Môn Toán 7 (sách Cánh diều) là tài liệu ôn tập bao gồm tới 12 đề thi khác nhau, tất cả đều được biên soạn kỹ lưỡng và bám sát hoàn toàn nội dung trong Sách giáo khoa Toán 7 Cánh diều. Đây là nguồn tài liệu quý giá, không chỉ giúp các em học sinh luyện tập chuyên sâu trước kỳ thi, mà còn là tư liệu tham khảo đắc lực để quý thầy cô tham khảo cấu trúc và xây dựng đề kiểm tra chất lượng. Mời quý thầy cô và các bạn tham khảo. Mời Tải về để xem trọn bộ.
Lưu ý: Dưới đây là một số đề thi mẫu, mời các bạn tải về xem trọn bộ 12 đề thi và đáp án trong file tải.
Đề thi học kì 1 Toán 7 Cánh diều - Đề 1
Câu 1: Kết quả của phép tính: 
\({{\left( -5 \right)}^{6}}:{{\left( -5 \right)}^{2}}\)
| \(A. {{\left( -5 \right)}^{4}}\) |
\(B. {{\left( -5 \right)}^{3}}\) |
| \(C. {{\left( -5 \right)}^{2}}\) |
\(D. {{\left( -5 \right)}^{8}}\) |
Câu 2: Số nào sau đây bằng \(\frac{3}{4}\)?
| \(A. \sqrt{\frac{{{\left( -9 \right)}^{2}}}{{{4}^{2}}}}\) |
\(B. \sqrt{\frac{{{1}^{2}}+{{2}^{2}}}{{{2}^{2}}}}\) |
| \(C. \sqrt{\frac{6}{{{2}^{2}}}:\frac{1}{{{2}^{3}}}}\) |
\(D. \sqrt{\frac{9}{16}}\) |
Câu 3: Cho biết x, y là hai đại lượng tỉ lệ nghịch. Biết x = -2 thì y = 8. Hỏi x = 3 thì y có giá trị bằng bao nhiêu?
| A. -12 | B. 12 |
| C. 24 | D. -24 |
Câu 4: Cho tam giác MNE có \(\widehat{M}={{65}^{0}},\widehat{E}=54\). Hỏi góc ngoài tại đỉnh N của tam giác MNE có số đo bằng bao nhiêu?
| \(A. {{120}^{0}}\) |
\(B. {{61}^{0}}\) |
| \(C. {{119}^{0}}\) |
\(D. {{74}^{0}}\) |
Câu 5: Nếu \(\frac{x}{5} = \frac{y}{7}\) và x – y = 4 thì:
A. x = 5; y = 7
B. x = 10, y = 14
C. x = - 10, y = -14
D. x = -9, y = - 21
Câu 6: Phát biểu nào sau đây sai?
A. Hai đường thẳng cùng vuông góc với một đường thẳng d thì hai đường thẳng đó song song với nhau.
B. Nếu \(a\bot d,b\bot d\) thì \(a//b\)
C. Nếu \(a\bot b,b\bot c\) thì \(a\bot c\)
D. Cho hai đường thẳng a và b song song với nhau. Nếu a vuông góc với đường thẳng c thì b cũng vuông góc với đường thẳng c.
Câu 7: Cho hình vẽ biết AE // BC. Số đo x, y là:
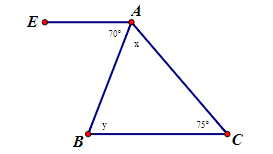
| A. \(x = \,{35^ \circ },y = {70^ \circ }\) |
B. \(x = \,{70^ \circ },y = {35^ \circ }\) |
| C. \(x = \,{45^ \circ },y = {70^ \circ }\) |
D. \(x = \,{70^ \circ },y = {45^ \circ }\) |
Câu 8: Kết quả của phép tính \(\dfrac{2}{3}.\dfrac{{ - 5}}{8}\) là:
| A. \(- \dfrac{3}{{11}}\) |
B. \(- \dfrac{7}{5}\) |
C. \(\dfrac{5}{{12}}\) |
D. \(- \dfrac{5}{{12}}\) |
Câu 9: Cho \(a{\rm{ }} + b-c \ne 0\) và \(\dfrac{a}{2} = \dfrac{b}{3} = \dfrac{c}{4}\) . Tính giá trị của \(H = \dfrac{{a + 2b + c}}{{a + b - c}}\)
| A. \(H = \dfrac{3}{4}\) |
B. \(H = \dfrac{4}{3}\) |
C. H = 12 | D. \(H = \dfrac{1}{{12}}\) |
Câu 10: Cho hình vẽ sau
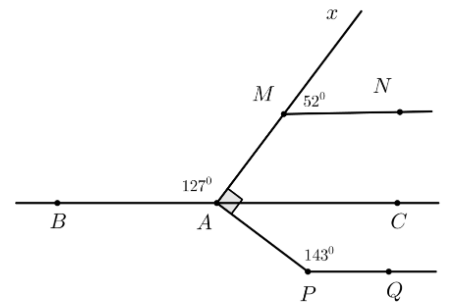
Biết \(\widehat {BAM} = {127^ \circ },\widehat {NMx} = {52^ \circ },\widehat {APQ} = {143^ \circ },AM \bot AP\) . Số đường thẳng song song với AB trong hình vẽ là
A. 1
B. 0
C. 2
D. 3
Phần II. Tự luận (7 điểm):
Bài 1: (2,0 điểm) Thực hiện phép tính:
\(a. 23\frac{1}{3}:\left( \frac{-5}{7} \right)-13\frac{1}{3}:\left( -\frac{5}{7} \right)\)\(b. 25.\left( \frac{-1}{5} \right)+\frac{1}{5}-2.{{\left( -\frac{1}{2} \right)}^{2}}-\sqrt{\frac{1}{4}}\)
Bài 2 (2,0 điểm): Tìm x biết:
| \(a. \frac{3}{4}-\frac{2}{5}x=\frac{29}{60}\) |
\(b. 6-\left| \frac{1}{2}-x \right|=\frac{2}{5}\) |
Bài 3: (1,5 điểm)
Tính diện tích của một hình chữ nhật biết các cạnh của nó tỉ lệ 3 : 5 và chiều dài hơn chiều rộng 18cm.
Bài 4: (1 điểm)
Một hộp đựng khẩu trang y tế được làm bằng bìa có dạng một hình hộp chữ nhật, kích thước như hình vẽ bên dưới.
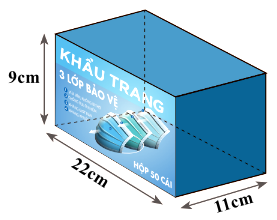
a) Hãy tính thể tích của hộp.
b) Tính diện tích bìa cứng dùng để làm hộp (bỏ qua mép dán).
Bài 5: (0,5 điểm)
Cho các số a,b,c thỏa mãn \(\frac{a}{{2020}} = \frac{b}{{2021}} = \frac{c}{{2022}}\). Chứng tỏ rằng: \(4\left( {a - b} \right)\left( {b - c} \right) = {\left( {c - a} \right)^2}.\)
***************
