Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm
VnDoc.com Lớp 7 Đề thi học kì 1 lớp 7

Đề thi học kì 1 Toán 7 Cánh diều - Đề 1

Đề thi Toán 7 học kì 1 có đáp án

Đề thi cuối kì 1 Toán 7 Cánh diều có đáp án

Mời thầy cô và các bạn tham khảo Đề thi cuối học kì 1 Toán 7 sách Cánh diều do VnDoc đăng tải sau đây. Đề thi Toán 7 học kì 1 năm 2023 được biên soạn bám sát nội dung học trong SGK Toán 7 Cánh diều. Đây không chỉ là tài liệu hay cho các em ôn luyện trước kỳ thi mà còn là tài liệu cho thầy cô tham khảo ra đề. Sau đây mời các bạn tham khảo chi tiết.

Đề kiểm tra học kì 1 Toán 7 Cánh diều

Câu 1: Kết quả của phép tính: {{\left( -5 \right)}^{6}}:{{\left( -5 \right)}^{2}}\({{\left( -5 \right)}^{6}}:{{\left( -5 \right)}^{2}}\)

A. {{\left( -5 \right)}^{4}}\(A. {{\left( -5 \right)}^{4}}\)B. {{\left( -5 \right)}^{3}}\(B. {{\left( -5 \right)}^{3}}\)
C. {{\left( -5 \right)}^{2}}\(C. {{\left( -5 \right)}^{2}}\)D. {{\left( -5 \right)}^{8}}\(D. {{\left( -5 \right)}^{8}}\)

Câu 2: Số nào sau đây bằng \frac{3}{4}\(\frac{3}{4}\)?

A. \sqrt{\frac{{{\left( -9 \right)}^{2}}}{{{4}^{2}}}}\(A. \sqrt{\frac{{{\left( -9 \right)}^{2}}}{{{4}^{2}}}}\)B. \sqrt{\frac{{{1}^{2}}+{{2}^{2}}}{{{2}^{2}}}}\(B. \sqrt{\frac{{{1}^{2}}+{{2}^{2}}}{{{2}^{2}}}}\)
C. \sqrt{\frac{6}{{{2}^{2}}}:\frac{1}{{{2}^{3}}}}\(C. \sqrt{\frac{6}{{{2}^{2}}}:\frac{1}{{{2}^{3}}}}\)D. \sqrt{\frac{9}{16}}\(D. \sqrt{\frac{9}{16}}\)

Câu 3: Cho biết x, y là hai đại lượng tỉ lệ nghịch. Biết x = -2 thì y = 8. Hỏi x = 3 thì y có giá trị bằng bao nhiêu?

A. -12B. 12
C. 24D. -24

Câu 4: Cho tam giác MNE có \widehat{M}={{65}^{0}},\widehat{E}=54\(\widehat{M}={{65}^{0}},\widehat{E}=54\). Hỏi góc ngoài tại đỉnh N của tam giác MNE có số đo bằng bao nhiêu?

A. {{120}^{0}}\(A. {{120}^{0}}\)B. {{61}^{0}}\(B. {{61}^{0}}\)
C. {{119}^{0}}\(C. {{119}^{0}}\)D. {{74}^{0}}\(D. {{74}^{0}}\)

 

Câu 5: Nếu \frac{x}{5} = \frac{y}{7}\(\frac{x}{5} = \frac{y}{7}\) và x – y = 4 thì:

A. x = 5; y = 7

B. x = 10, y = 14

C. x = - 10, y = -14

D. x = -9, y = - 21

Câu 6: Phát biểu nào sau đây sai?

A. Hai đường thẳng cùng vuông góc với một đường thẳng d thì hai đường thẳng đó song song với nhau.

B. Nếu a\bot d,b\bot d\(a\bot d,b\bot d\) thì a//b\(a//b\)

C. Nếu a\bot b,b\bot c\(a\bot b,b\bot c\) thì a\bot c\(a\bot c\)

D. Cho hai đường thẳng a và b song song với nhau. Nếu a vuông góc với đường thẳng c thì b cũng vuông góc với đường thẳng c.

Câu 7: Cho hình vẽ biết AE // BC. Số đo x, y là:

A. x = \,{35^ \circ },y = {70^ \circ }\(x = \,{35^ \circ },y = {70^ \circ }\)B. x = \,{70^ \circ },y = {35^ \circ }\(x = \,{70^ \circ },y = {35^ \circ }\)
C. x = \,{45^ \circ },y = {70^ \circ }\(x = \,{45^ \circ },y = {70^ \circ }\)D. x = \,{70^ \circ },y = {45^ \circ }\(x = \,{70^ \circ },y = {45^ \circ }\)

Câu 8: Kết quả của phép tính \dfrac{2}{3}.\dfrac{{ - 5}}{8}\(\dfrac{2}{3}.\dfrac{{ - 5}}{8}\) là:

A. - \dfrac{3}{{11}}\(- \dfrac{3}{{11}}\)B. - \dfrac{7}{5}\(- \dfrac{7}{5}\)C. \dfrac{5}{{12}}\(\dfrac{5}{{12}}\)D. - \dfrac{5}{{12}}\(- \dfrac{5}{{12}}\)

Câu 9: Cho a{\rm{ }} + b-c \ne 0\(a{\rm{ }} + b-c \ne 0\) và \dfrac{a}{2} = \dfrac{b}{3} = \dfrac{c}{4}\(\dfrac{a}{2} = \dfrac{b}{3} = \dfrac{c}{4}\) . Tính giá trị của H = \dfrac{{a + 2b + c}}{{a + b - c}}\(H = \dfrac{{a + 2b + c}}{{a + b - c}}\)

A. H = \dfrac{3}{4}\(H = \dfrac{3}{4}\)B. H = \dfrac{4}{3}\(H = \dfrac{4}{3}\)C. H = 12D. H = \dfrac{1}{{12}}\(H = \dfrac{1}{{12}}\)

Câu 10: Cho hình vẽ sau

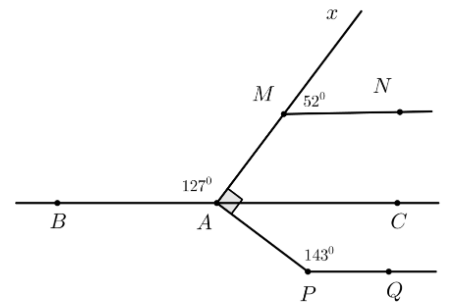
Biết \widehat {BAM} = {127^ \circ },\widehat {NMx} = {52^ \circ },\widehat {APQ} = {143^ \circ },AM \bot AP\(\widehat {BAM} = {127^ \circ },\widehat {NMx} = {52^ \circ },\widehat {APQ} = {143^ \circ },AM \bot AP\) . Số đường thẳng song song với AB trong hình vẽ là

A. 1

B. 0

C. 2

D. 3

Phần II. Tự luận (7 điểm):

Bài 1: (2,0 điểm) Thực hiện phép tính:

a. 23\frac{1}{3}:\left( \frac{-5}{7} \right)-13\frac{1}{3}:\left( -\frac{5}{7} \right)\(a. 23\frac{1}{3}:\left( \frac{-5}{7} \right)-13\frac{1}{3}:\left( -\frac{5}{7} \right)\)
b. 25.\left( \frac{-1}{5} \right)+\frac{1}{5}-2.{{\left( -\frac{1}{2} \right)}^{2}}-\sqrt{\frac{1}{4}}\(b. 25.\left( \frac{-1}{5} \right)+\frac{1}{5}-2.{{\left( -\frac{1}{2} \right)}^{2}}-\sqrt{\frac{1}{4}}\)
Bài 2 (2,0 điểm): Tìm x biết:

a. \frac{3}{4}-\frac{2}{5}x=\frac{29}{60}\(a. \frac{3}{4}-\frac{2}{5}x=\frac{29}{60}\)b. 6-\left| \frac{1}{2}-x \right|=\frac{2}{5}\(b. 6-\left| \frac{1}{2}-x \right|=\frac{2}{5}\)

Bài 3: (1,5 điểm)

Tính diện tích của một hình chữ nhật biết các cạnh của nó tỉ lệ 3 : 5 và chiều dài hơn chiều rộng 18cm.

Bài 4: (1 điểm)

Một hộp đựng khẩu trang y tế được làm bằng bìa có dạng một hình hộp chữ nhật, kích thước như hình vẽ bên dưới.

a) Hãy tính thể tích của hộp.

b) Tính diện tích bìa cứng dùng để làm hộp (bỏ qua mép dán).

Bài 5: (0,5 điểm)

Cho các số a,b,c thỏa mãn \frac{a}{{2020}} = \frac{b}{{2021}} = \frac{c}{{2022}}\(\frac{a}{{2020}} = \frac{b}{{2021}} = \frac{c}{{2022}}\). Chứng tỏ rằng: 4\left( {a - b} \right)\left( {b - c} \right) = {\left( {c - a} \right)^2}.\(4\left( {a - b} \right)\left( {b - c} \right) = {\left( {c - a} \right)^2}.\)

Đáp án đề thi học kì 1 Toán 7 Cánh diều

I. Phần trắc nghiệm

Câu 1. ACâu 2. DCâu 3. ACâu 4. CCâu 5. D
Câu 6. CCâu 7. ACâu 8. DCâu 9. CCâu 10. A

Phần II. Tự luận (7 điểm):

Bài 1

a. 23\frac{1}{3}:\left( \frac{-5}{7} \right)-13\frac{1}{3}:\left( -\frac{5}{7} \right)\(23\frac{1}{3}:\left( \frac{-5}{7} \right)-13\frac{1}{3}:\left( -\frac{5}{7} \right)\)

\begin{align} & =\left( 23\frac{1}{3}-13\frac{1}{3} \right):\left( \frac{-5}{7} \right) \\ & =\left( \frac{70}{3}-\frac{40}{3} \right).\frac{-7}{5} \\ & =10.\frac{-7}{5}=-14 \\ \end{align}\(\begin{align} & =\left( 23\frac{1}{3}-13\frac{1}{3} \right):\left( \frac{-5}{7} \right) \\ & =\left( \frac{70}{3}-\frac{40}{3} \right).\frac{-7}{5} \\ & =10.\frac{-7}{5}=-14 \\ \end{align}\)

b. 25.\left( \frac{-1}{5} \right)+\frac{1}{5}-2.{{\left( -\frac{1}{2} \right)}^{2}}-\sqrt{\frac{1}{4}}\(25.\left( \frac{-1}{5} \right)+\frac{1}{5}-2.{{\left( -\frac{1}{2} \right)}^{2}}-\sqrt{\frac{1}{4}}\)

\begin{align} & =\frac{-25}{5}+\frac{1}{5}-2.\frac{1}{4}-\frac{1}{2} \\ & =\frac{-24}{5}-\frac{1}{2}-\frac{1}{2}=\frac{-24}{5}-1 \\ & =\frac{-24-5}{5}=\frac{-29}{5} \\ \end{align}\(\begin{align} & =\frac{-25}{5}+\frac{1}{5}-2.\frac{1}{4}-\frac{1}{2} \\ & =\frac{-24}{5}-\frac{1}{2}-\frac{1}{2}=\frac{-24}{5}-1 \\ & =\frac{-24-5}{5}=\frac{-29}{5} \\ \end{align}\)

Bài 2

a. \frac{3}{4}-\frac{2}{5}x=\frac{29}{60}\(\frac{3}{4}-\frac{2}{5}x=\frac{29}{60}\)

\begin{align} & \frac{-2}{5}x=\frac{29}{60}-\frac{3}{4} \\ & \frac{-2}{5}x=-\frac{4}{15} \\ & x=-\frac{4}{15}:\frac{-2}{5} \\ & x=-\frac{4}{15}.\frac{5}{-2}=\frac{2}{3} \\ \end{align}\(\begin{align} & \frac{-2}{5}x=\frac{29}{60}-\frac{3}{4} \\ & \frac{-2}{5}x=-\frac{4}{15} \\ & x=-\frac{4}{15}:\frac{-2}{5} \\ & x=-\frac{4}{15}.\frac{5}{-2}=\frac{2}{3} \\ \end{align}\)

Vậy x=\frac{2}{3}\(x=\frac{2}{3}\)

b. 6-\left| \frac{1}{2}-x \right|=\frac{2}{5}\(6-\left| \frac{1}{2}-x \right|=\frac{2}{5}\)

\begin{align} & \left| \frac{1}{2}-x \right|=6-\frac{2}{5} \\ & \left| \frac{1}{2}-x \right|=\frac{28}{5} \\ \end{align}\(\begin{align} & \left| \frac{1}{2}-x \right|=6-\frac{2}{5} \\ & \left| \frac{1}{2}-x \right|=\frac{28}{5} \\ \end{align}\)

Trường hợp 1: \frac{1}{2}-x=\frac{28}{5}\Rightarrow x=\frac{1}{2}-\frac{28}{5}=\frac{-51}{10}\(\frac{1}{2}-x=\frac{28}{5}\Rightarrow x=\frac{1}{2}-\frac{28}{5}=\frac{-51}{10}\)

Trường hợp 2: \frac{1}{2}-x=-\frac{28}{5}\Rightarrow x=\frac{1}{2}+\frac{28}{5}=\frac{61}{10}\(\frac{1}{2}-x=-\frac{28}{5}\Rightarrow x=\frac{1}{2}+\frac{28}{5}=\frac{61}{10}\)

Vậy x=\frac{-51}{10}\(x=\frac{-51}{10}\) hoặc x=\frac{61}{10}\(x=\frac{61}{10}\)

Bài 3

Gọi chiều rộng của hình chữ nhật là x (cm)

Chiều dài của hình chữ nhật là y (cm)

Chiều dài và chiều rộng của hình chữ nhật có tỉ lệ 3 : 5 nên ta có:

\frac{x}{3}=\frac{y}{5}\(\frac{x}{3}=\frac{y}{5}\) (1)

Chiều dài hơn chiều rộng 18cm nên ta có:

y-x=18\(y-x=18\) (2)

Từ (1) và (2) và áp dụng tính chất của dãy tỉ số bằng nhau ta có:

\begin{align} & \frac{x}{3}=\frac{y}{5}=\frac{y-x}{5-3}=\frac{18}{2}=9 \\ & \Rightarrow \frac{x}{3}=9\Rightarrow x=9.3=27cm \\ & \Rightarrow \frac{y}{5}=9\Rightarrow y=9.5=45cm \\ \end{align}\(\begin{align} & \frac{x}{3}=\frac{y}{5}=\frac{y-x}{5-3}=\frac{18}{2}=9 \\ & \Rightarrow \frac{x}{3}=9\Rightarrow x=9.3=27cm \\ & \Rightarrow \frac{y}{5}=9\Rightarrow y=9.5=45cm \\ \end{align}\)

Diện tích hình chữ nhật là: 27 . 45 = 1215 c{{m}^{2}}\(c{{m}^{2}}\)

Vậy diện tích hình chữ nhật là: 1215

Bài 4

Cách giải:

a) Thể tích của hộp là: 22.11.9 = 2178\,\left( {c{m^3}} \right)\(22.11.9 = 2178\,\left( {c{m^3}} \right)\)

b) Diện tích bìa cứng dùng để là hộp bao gồm diện tích xung quanh và tổng diện tích hai đáy của hộp.

Diện tích xung quanh của hộp là: {S_{xq}} = 2.\left( {22 + 11} \right).9 = 594\,\left( {c{m^2}} \right)\({S_{xq}} = 2.\left( {22 + 11} \right).9 = 594\,\left( {c{m^2}} \right)\)

Diện tích hai đáy của hộp là: S = 2.22.11 = 484\,\left( {c{m^2}} \right)\(S = 2.22.11 = 484\,\left( {c{m^2}} \right)\)

Diện tích bìa cứng dùng để làm hộp là: {S_{xq}} + S = 594 + 484 = 1078\,\left( {c{m^2}} \right)\({S_{xq}} + S = 594 + 484 = 1078\,\left( {c{m^2}} \right)\)

Bài 5

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

\frac{a}{{2020}} = \frac{b}{{2021}} = \frac{c}{{2022}} = \frac{{a - b}}{{2020 - 2021}} = \frac{{b - c}}{{2021 - 2022}} = \frac{{c - a}}{{2022 - 2020}}\(\frac{a}{{2020}} = \frac{b}{{2021}} = \frac{c}{{2022}} = \frac{{a - b}}{{2020 - 2021}} = \frac{{b - c}}{{2021 - 2022}} = \frac{{c - a}}{{2022 - 2020}}\)

Suy ra \frac{{a - b}}{{ - 1}} = \frac{{b - c}}{{ - 1}} = \frac{{c - a}}{2}\(\frac{{a - b}}{{ - 1}} = \frac{{b - c}}{{ - 1}} = \frac{{c - a}}{2}\) hay c - a = - 2\left( {a - b} \right) = - 2\left( {b - c} \right)\(c - a = - 2\left( {a - b} \right) = - 2\left( {b - c} \right)\)

Do đó, \left( {c - a} \right).\left( {c - a} \right) = \left[ { - 2\left( {a - b} \right)} \right].\left[ { - 2\left( {b - c} \right)} \right]\(\left( {c - a} \right).\left( {c - a} \right) = \left[ { - 2\left( {a - b} \right)} \right].\left[ { - 2\left( {b - c} \right)} \right]\)

Suy ra {\left( {c - a} \right)^2} = 4\left( {a - b} \right)\left( {b - c} \right) (đpcm)\({\left( {c - a} \right)^2} = 4\left( {a - b} \right)\left( {b - c} \right) (đpcm)\)

Bộ đề thi học kì 1 lớp 7 môn Toán

...................................................

Để chuẩn bị tốt cho kì thi học kì 1 lớp 7 sắp tới, các em học sinh cần thực hành luyện đề đề làm quen với nhiều dạng đề thi khác nhau và nắm được cấu trúc đề thi. VnDoc giới thiệu tới các bạn chuyên mục Đề thi học kì 1 lớp 7 với đầy đủ các môn. Đây là tài liệu hay cho thầy cô tham khảo ra đề, cũng là nguồn tài liệu để các em học sinh ôn luyện trước kì thi. Mời thầy cô và các em tham khảo.

Chia sẻ, đánh giá bài viết
6
1.213 Bài viết đã được lưu
Mục lục
Tìm thêm: đề thi học kì 1 toán 7 đề kiểm tra học kì 1 toán 7 đề cương ôn tập học kì 1 toán 7
Sắp xếp theo
Xóa Đăng nhập để Gửi
    Đề thi học kì 1 lớp 7

    Tham khảo thêm

    🖼️

    Gợi ý cho bạn

    Xem thêm
    🖼️

    Đề thi học kì 1 lớp 7

    Xem thêm